
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問11 [20番](2019年11月試験)
テーマ
- 歪度
- 尖度
正答
選択肢⑤
解答例
歪度と尖度は確率分布の平均μと分散σ^2(標準偏差σ)を用いて計算される分布の形状を示唆する指標になります。具体的には以下のような式(※)になります。

上記の通り、歪度は「3乗」を用いた指標で分布の対称性を示す指標になります。一方の尖度は「4乗」を用いた指標で分布の鋭さを示す指標になります。
[記述Ⅰ]:歪度(および尖度)は分布の平均μに依存しませんので「誤り」です。
[記述Ⅱ]:右に裾が長い分布のとき歪度は正の値を取りますので「誤り」です。
[記述Ⅲ]:歪度が0となるのは分布が左右対称の場合です。多峰の分布であるかどうかで歪度が0であるかが決まるわけではありません。よって「誤り」です。
補足
- 歪度は「3乗」で計算される指標です。マイナス側(下側・左側)に裾が長い分布のときは、歪度はマイナスになります。
(※) 尖度は「-3」をつけない定義もあります。「-3」をつけることで正規分布のときに0になります。
(20番、以上)
問12 [21番](2019年11月試験)
テーマ
- 一致推定量(一致性)
- 不偏推定量(不偏性)
正答
選択肢⑤
解答例
[記述Ⅰ]:1つ目の推定量は、n個の観測値のなかから1個目とn個目の2個の観測値のみを抽出し、その2個の観測値を足して2で割ったものです。その期待値は以下のようになります。
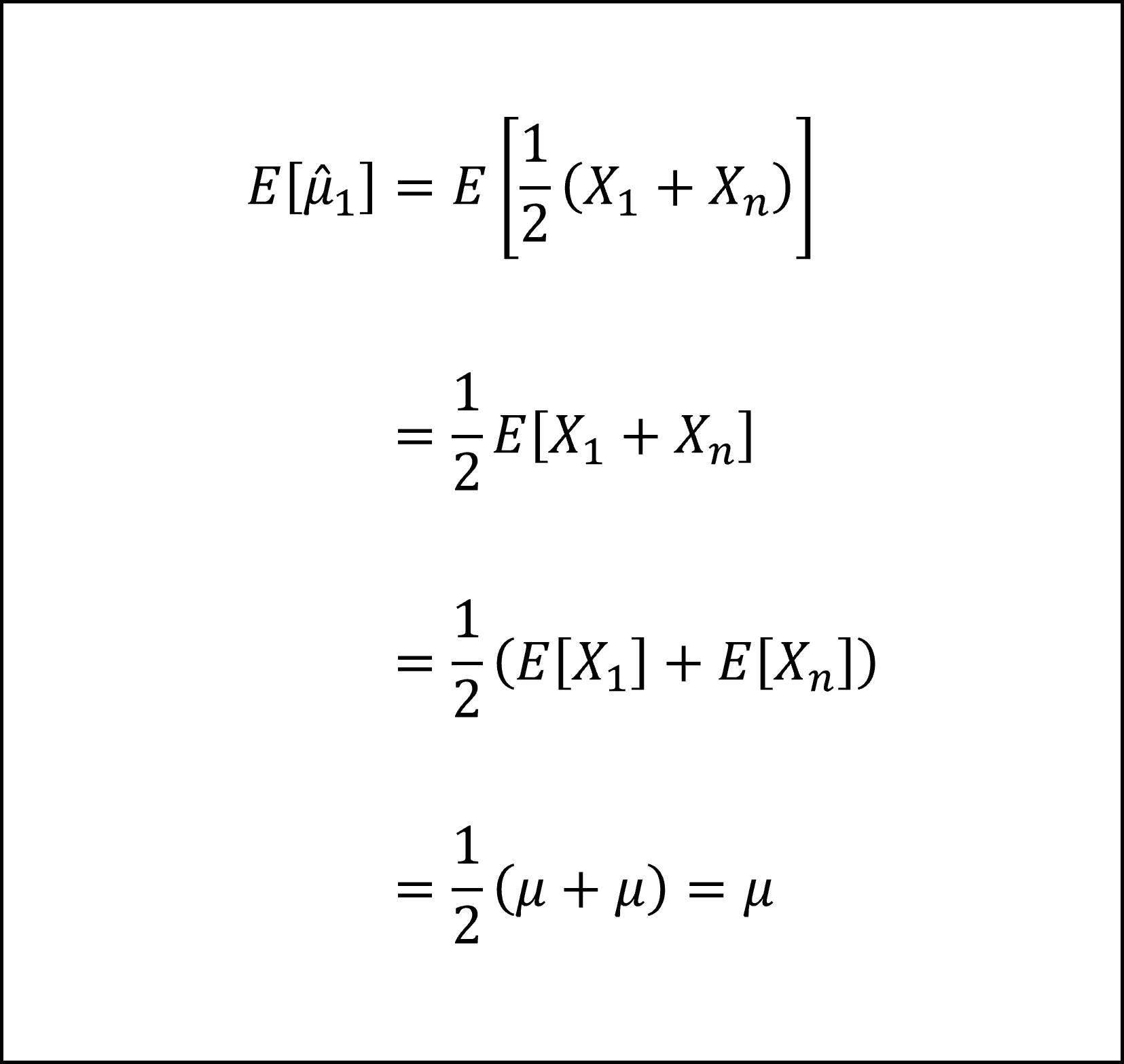
期待値が母数μに等しく不偏推定量になりますので記述Ⅰは「正しい」です。
[記述Ⅱ]:一致性は「サンプルサイズnを極めて大きくしたときに推定量が母数に近づいていく(確率収束する)」性質です。
1つ目の推定量は2個の観測値を足して2で割ったものですので、サンプルサイズnを大きくしても母数に近づいていくわけではなく、一致性は認められません。よって記述Ⅱは「誤り」です。
[記述Ⅲ]:2つ目の推定量は、n個の観測値のなかから1個目とn個目以外のn-2個の観測値を合計してn-2で割ったもので、期待値は以下のようになります。
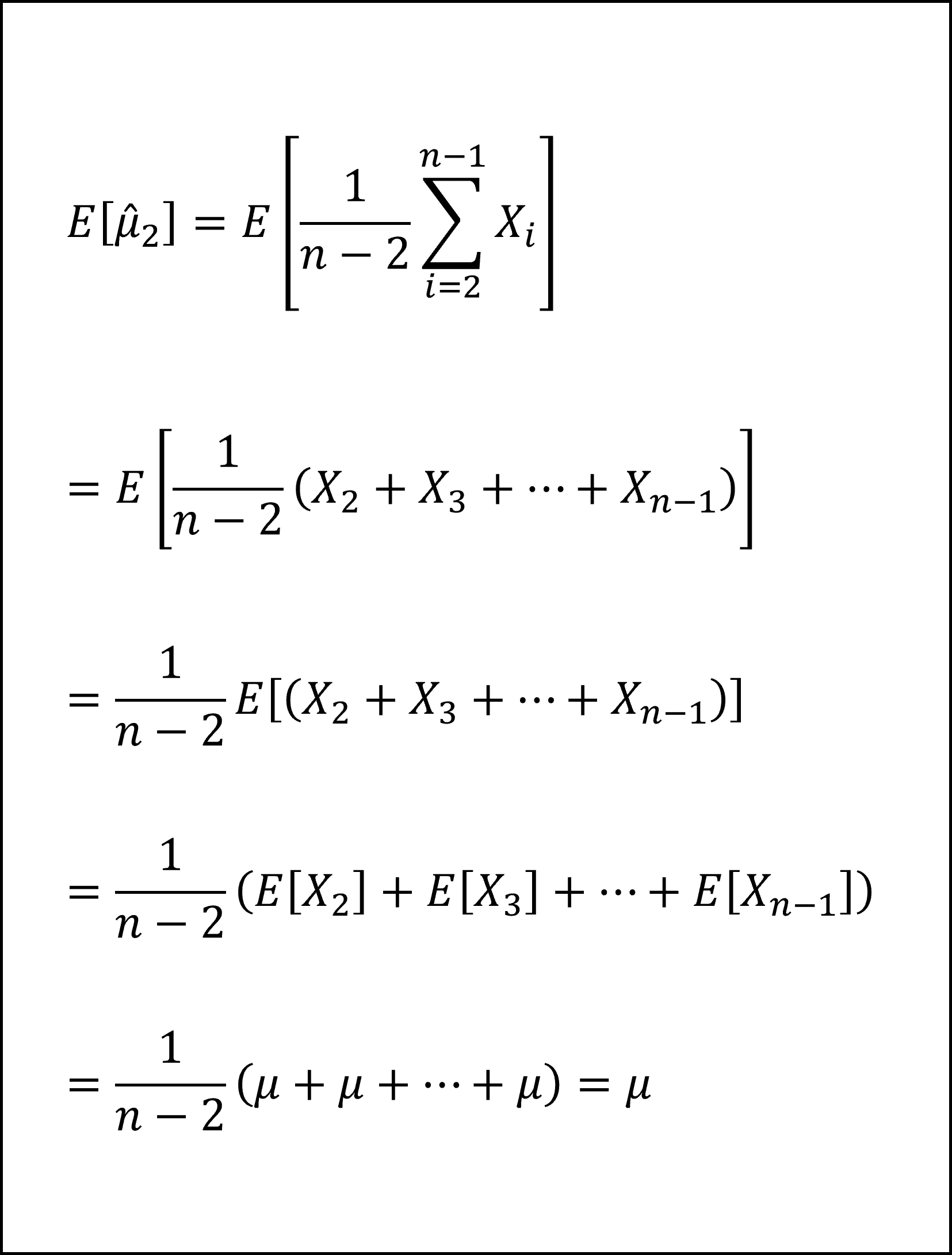
期待値が母数μに等しくなりますので記述Ⅲは「正しい」です。
[記述Ⅳ]:2つ目の推定量はn-2個の観測値を用いて計算されていますので、サンプルサイズnを大きくしていくと、推定量の分散は小さくなっていきます。サンプルサイズnを極めて大きくしたときには、推定量の分散は極めて小さく(ほぼ0に)なり、母数に近似(確率収束)します。したがって、2つ目の推定量には一致性が認められますので、記述Ⅳは「正しい」です。
補足
一致性については厳密にはチェビシェフの不等式を用いて確認する必要がありますが、上記のように「サンプルサイズnが大きいほど推定量の分散は小さくなる→nが極めて大きいときには推定量の分散が極めて小さく(ほぼ0)になって母数に近似する」と簡略化して考えて大丈夫です。
(21番、以上)
問13 [22番](2019年11月試験)
テーマ
- 母比率の区間推定
- 信頼区間
正答
選択肢⑤
解答例
A候補に投票する人の数をX人とすると、XはA候補の得票率をp、投票者の総数をnとする二項分布にしたがいます。二項分布の期待値(平均)はnp、分散はnp(1-p)ですので、Xの分布を以下のように表記できます。
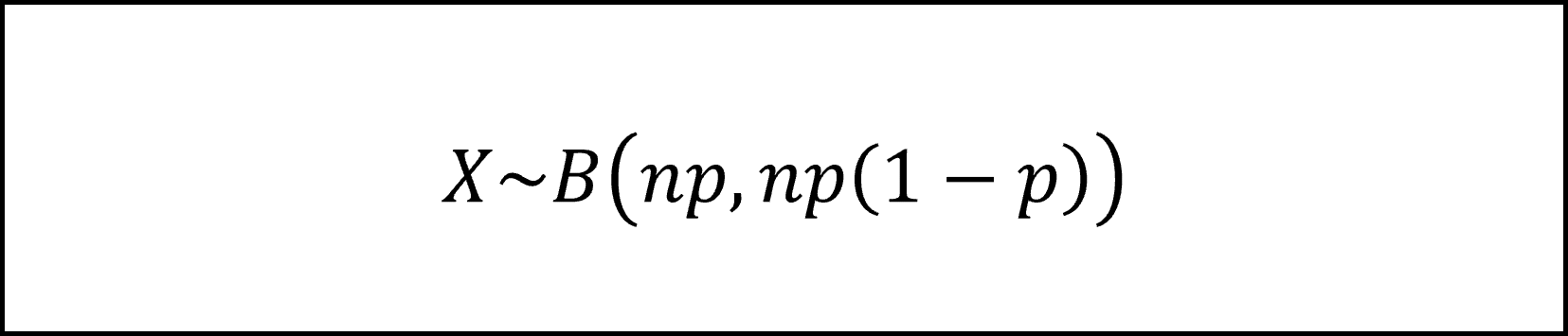
問題文より二項分布は正規分布にしたがいますので、
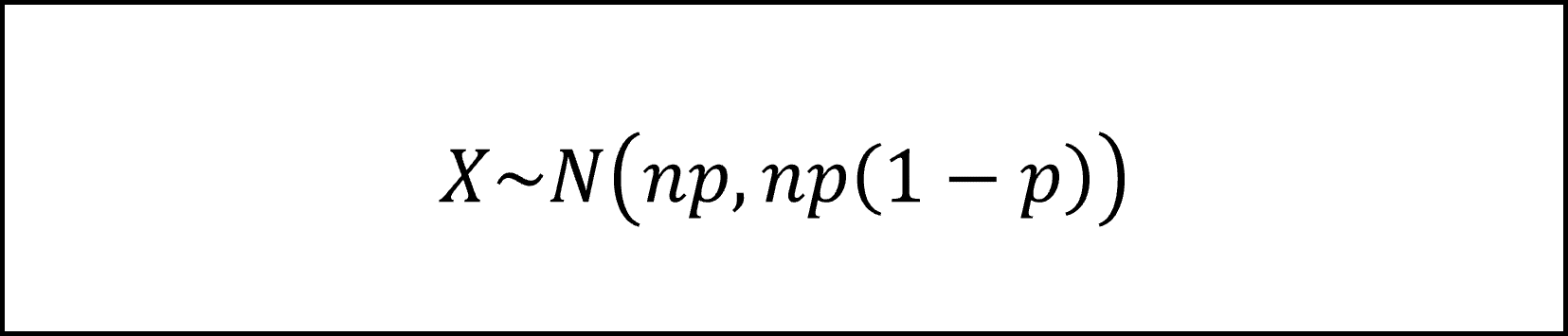
となり、ここで左辺のXをnで割って標本比率のかたちに整理すると以下のようになります。
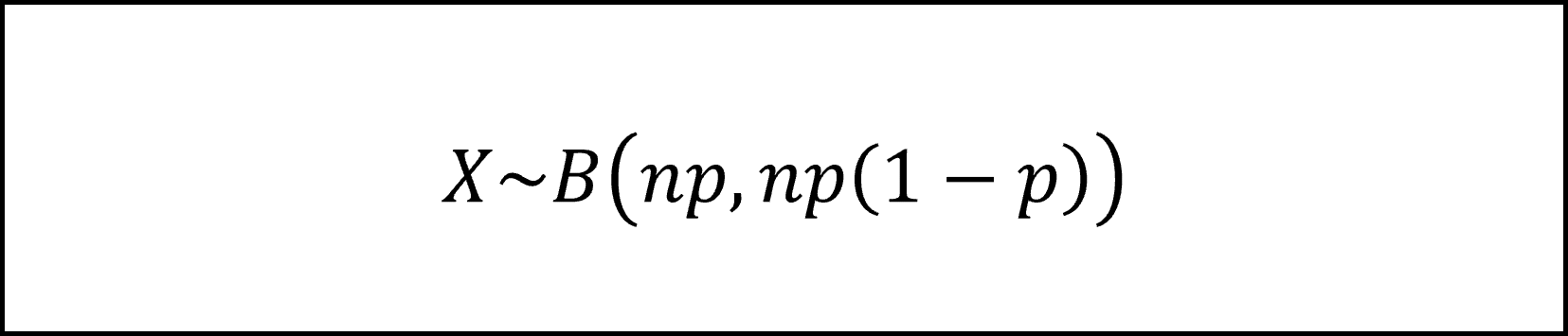
さらに(1)式を標準正規分布にしたがうかたちに整理(標準化)すると
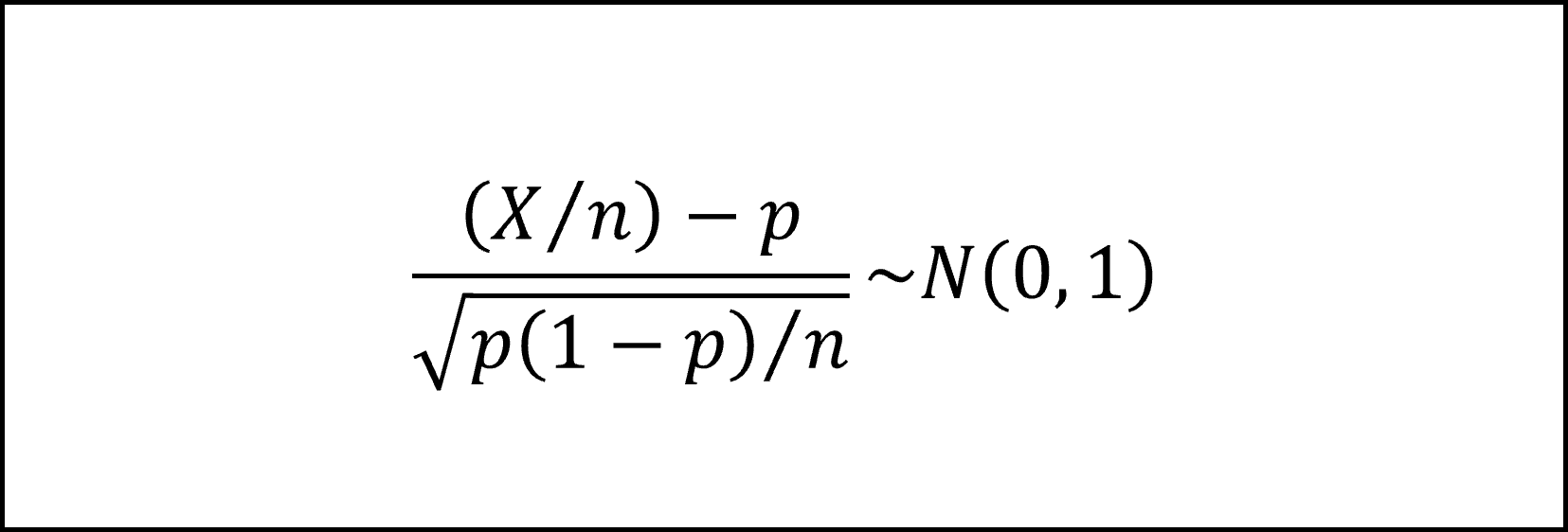
となります。
標準正規分布の付表より
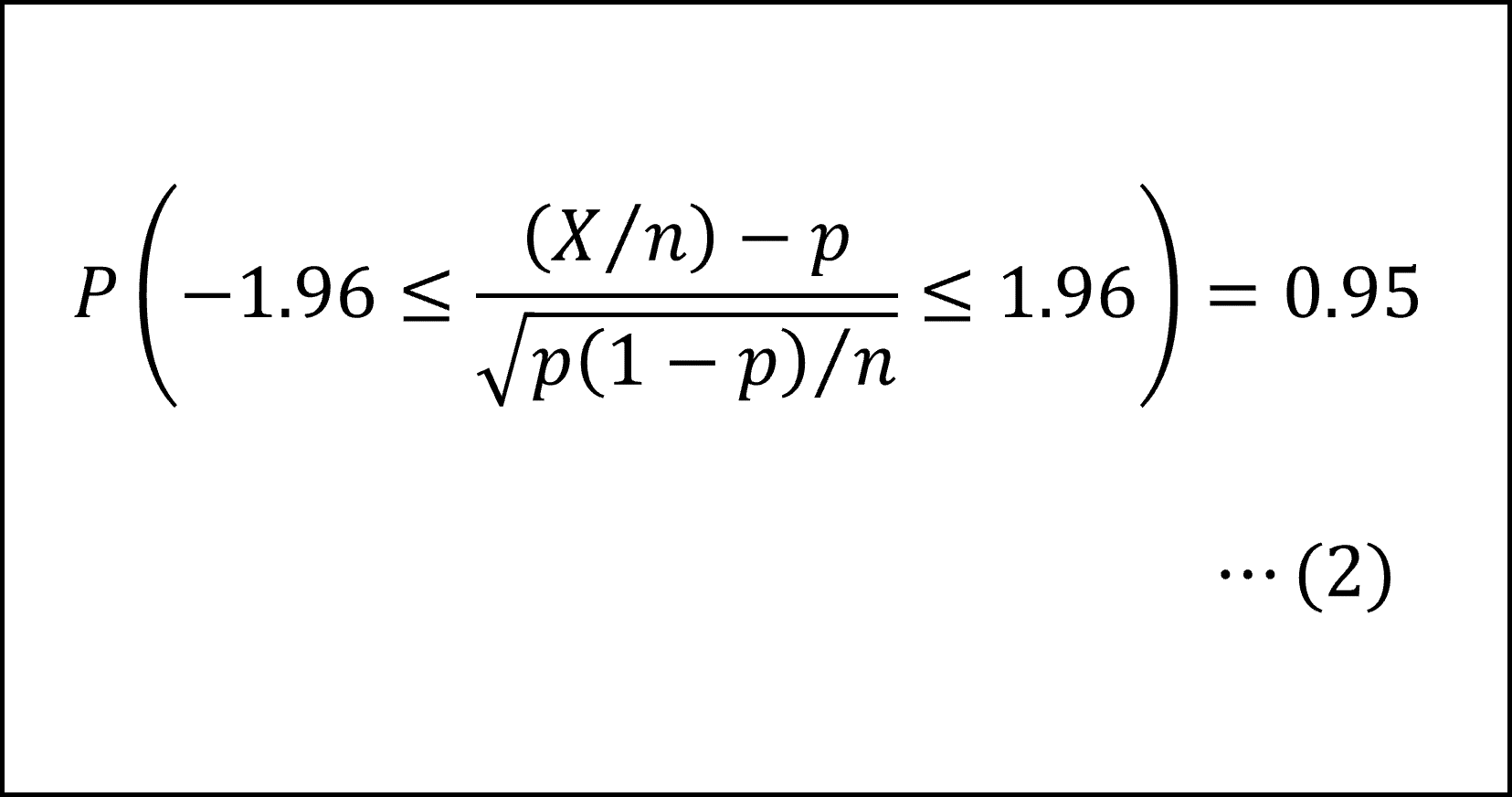
ですので、n=100、X=54を代入して、(2)式の不等式を整理すると
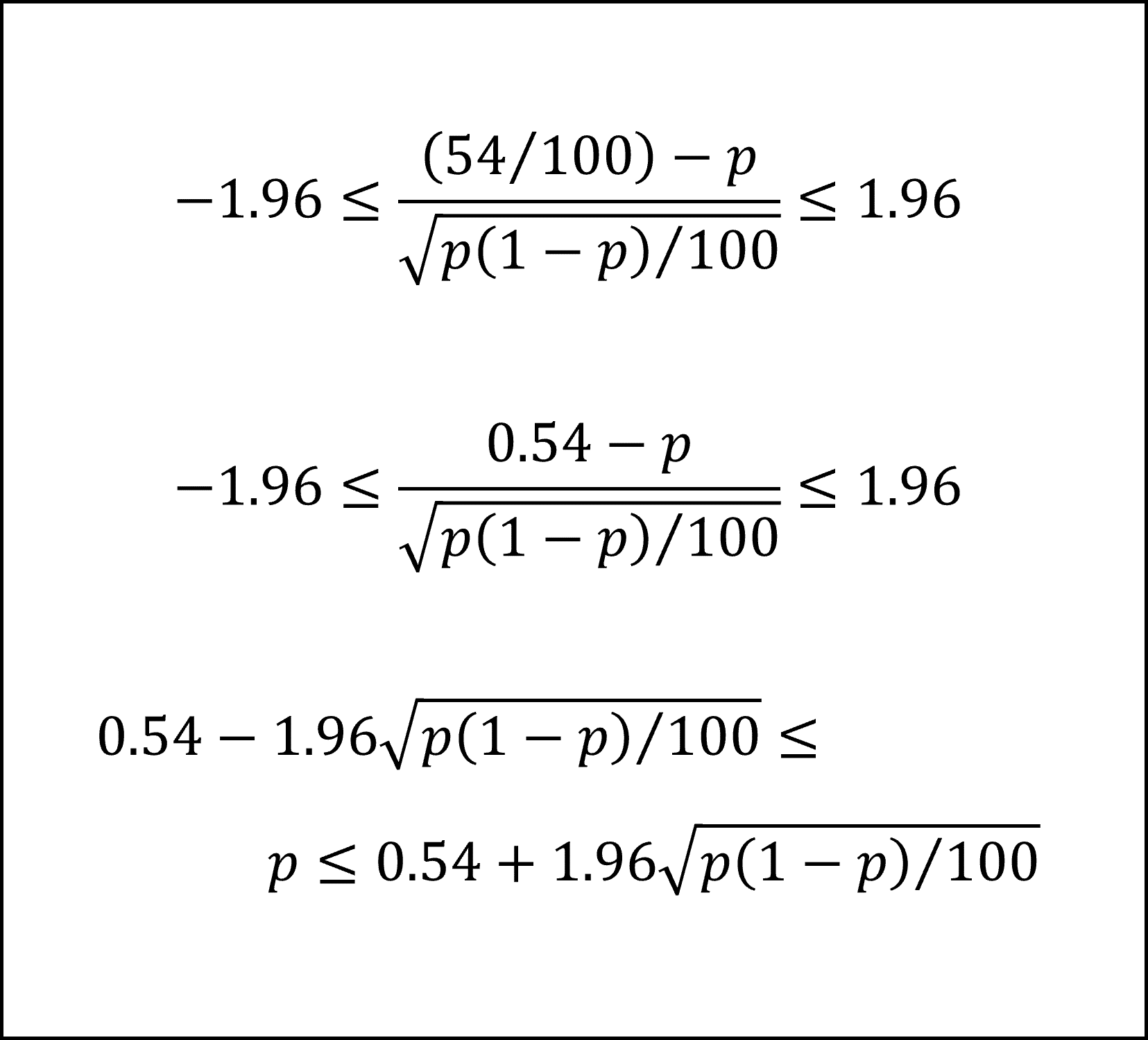
となります。ここで、平方根のなかの p について、近似計算法により標本比率 X/n =54/100=0.54を代入すると

となり(途中計算は適宜四捨五入してます)、A候補の得票率pの95%信頼区間は0.54±0.098となります。
補足
- 母比率の区間推定は二項分布→正規分布→標準正規分布という流れを理解できていれば、信頼区間の公式を覚えていなくても問題ありません(むしろ何がどんな分布にしたがうかという整理の方が大切です)。
- また、母比率の区間推定は小数点以下の計算でミスをしやすいので注意しましょう。
(22番、以上)
問14 [23,24番](2019年11月試験)
テーマ
- 非正規母集団
- 相対度数
- 中央値
- 中心極限定理
正答
[23番]選択肢③ [24番]選択肢③
解答例
[23番]中央値は全体の真ん中の順位の値です。したがって、中央値は累積の相対度数が50%となる階級にあります。
与えられた相対度数分布表より「400万円未満」までの累積相対度数が46.5%で、「500万円未満」までの累積相対度数が56.9%です。
したがって中央値は「400万円以上500万円未満」の階級にあり、中央値の「半分」は「200万円以上250万円未満」となります。
相対度数分布表より「200万円未満」までの累積相対度数が19.6%で、「300万円未満」までの累積相対度数が33.3%ですので、中央値の半分に満たない所得の世帯の割合は「19.6%以上33.3%以下」と言えます。
[24番]標本の大きさ n が十分に大きいとき、中心極限定理によって(母集団の分布にかかわらず)標本平均がしたがう分布は正規分布に近似します。
また、問題文中のZは標本平均を標準化したものですので、Zは標準正規分布にしたがいます。したがって、選択肢③が正答になります。
補足
所得(※)の中央値の半分を貧困ライン(貧困線)とし、その貧困ラインを下回る世帯の割合を相対的貧困率と呼びます(※一般には「世帯の可処分所得を世帯人数の平方根で割って調整した所得」を用います)。
(23,24番、以上)
問15 [25,26番](2019年11月試験)
テーマ
- 母比率の区間推定
- 二項分布
- 正規分布
- 中心極限定理
正答
[25番]選択肢④ [26番]選択肢②
解答例
[25番]標本調査における標本の大きさをn人、政策の支持者の数をx人、政策の支持率(母比率)をpとすると、Xは以下の二項分布にしたがいます。
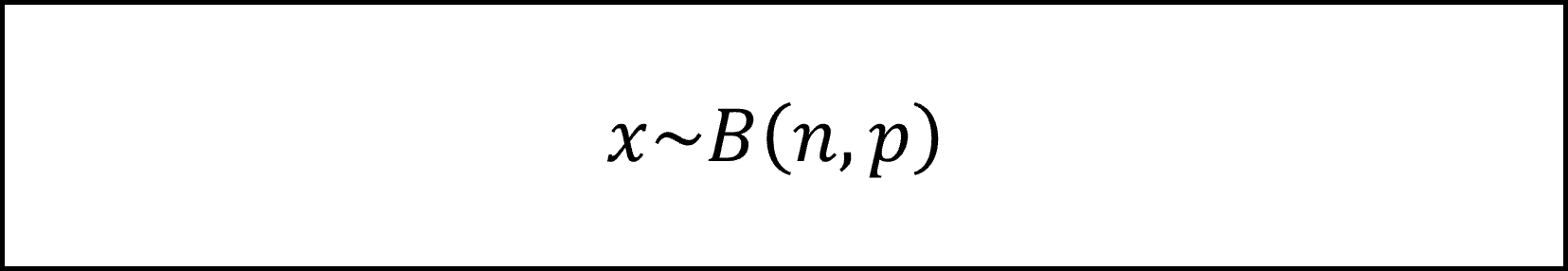
問題文より二項分布は近似的に正規分布にしたがいますので、支持者の数xおよび支持者の比率(標本比率)x/nの分布は以下のように整理できます。
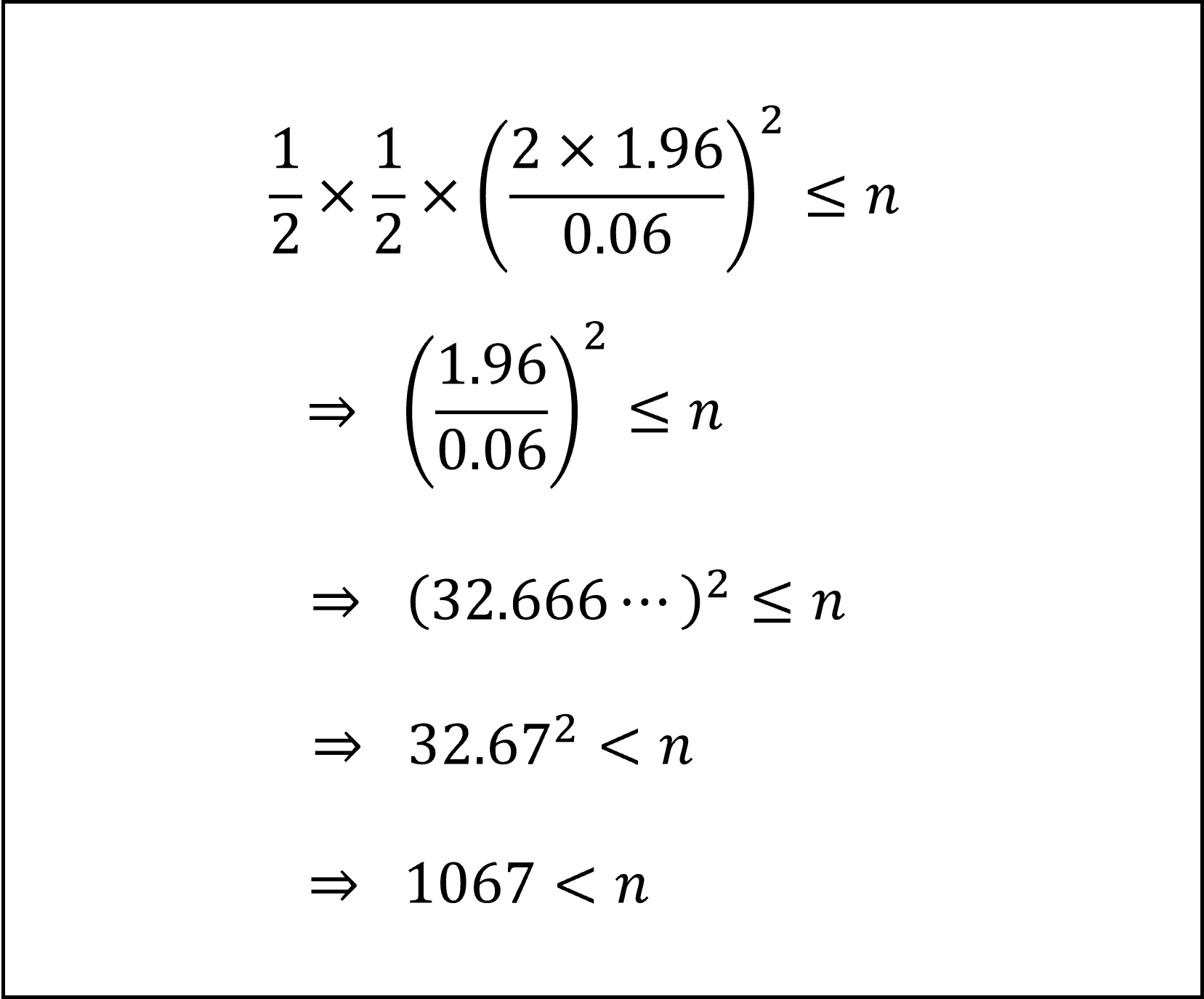
ここで、標準正規分布の付表より
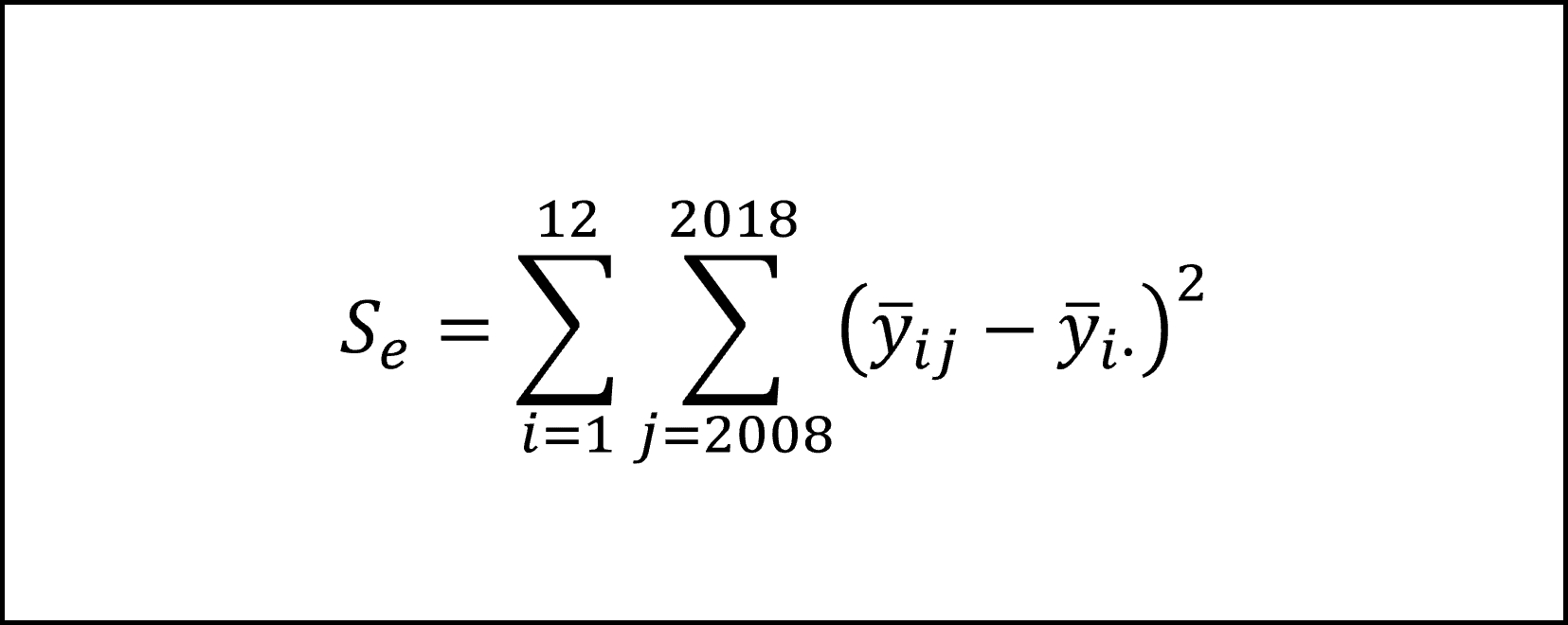
となりますので、支持率pの95%信頼区間を以下のように整理できます。
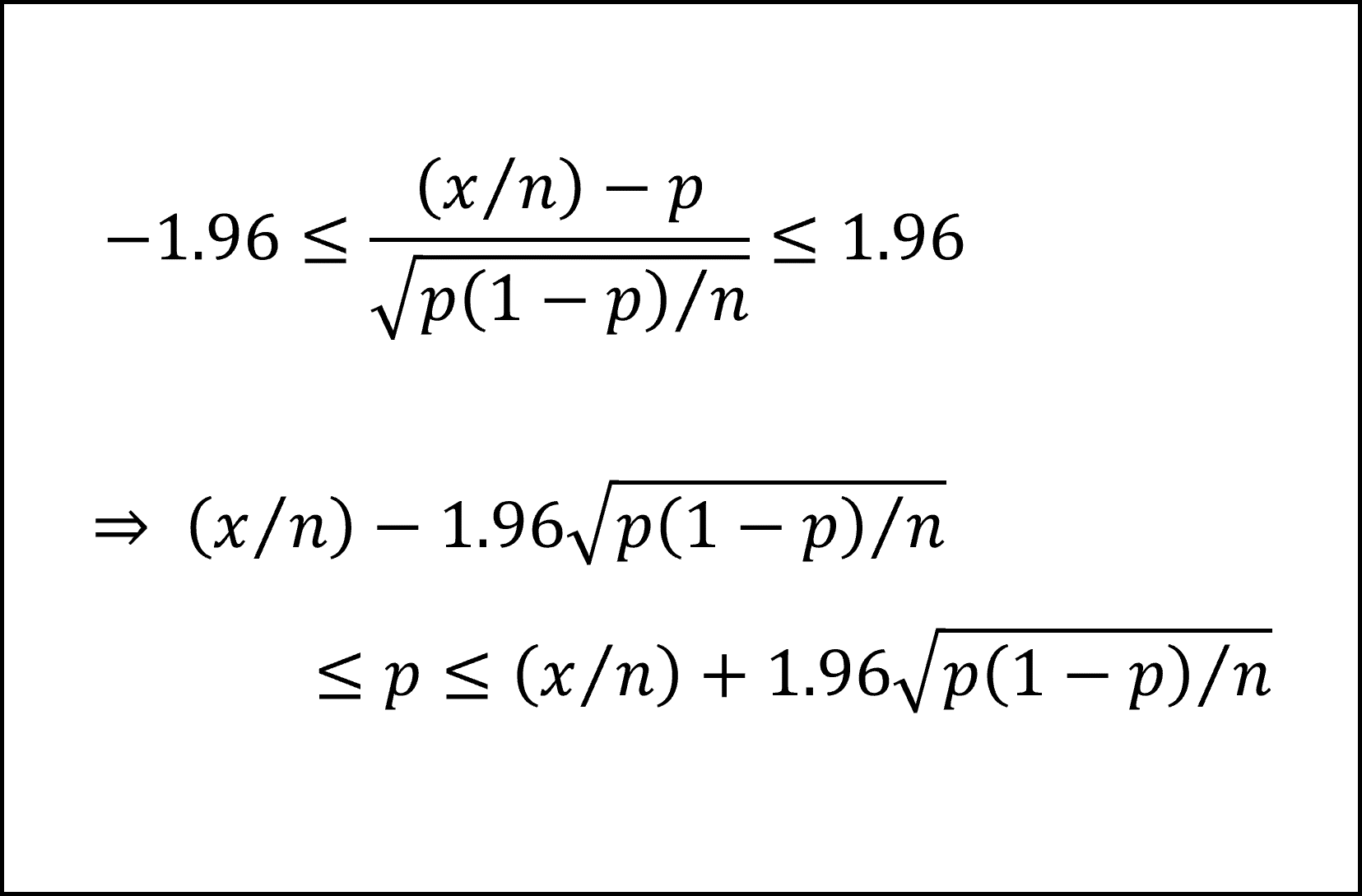
ここで、信頼区間の幅が6%(=0.06)以下となるためには
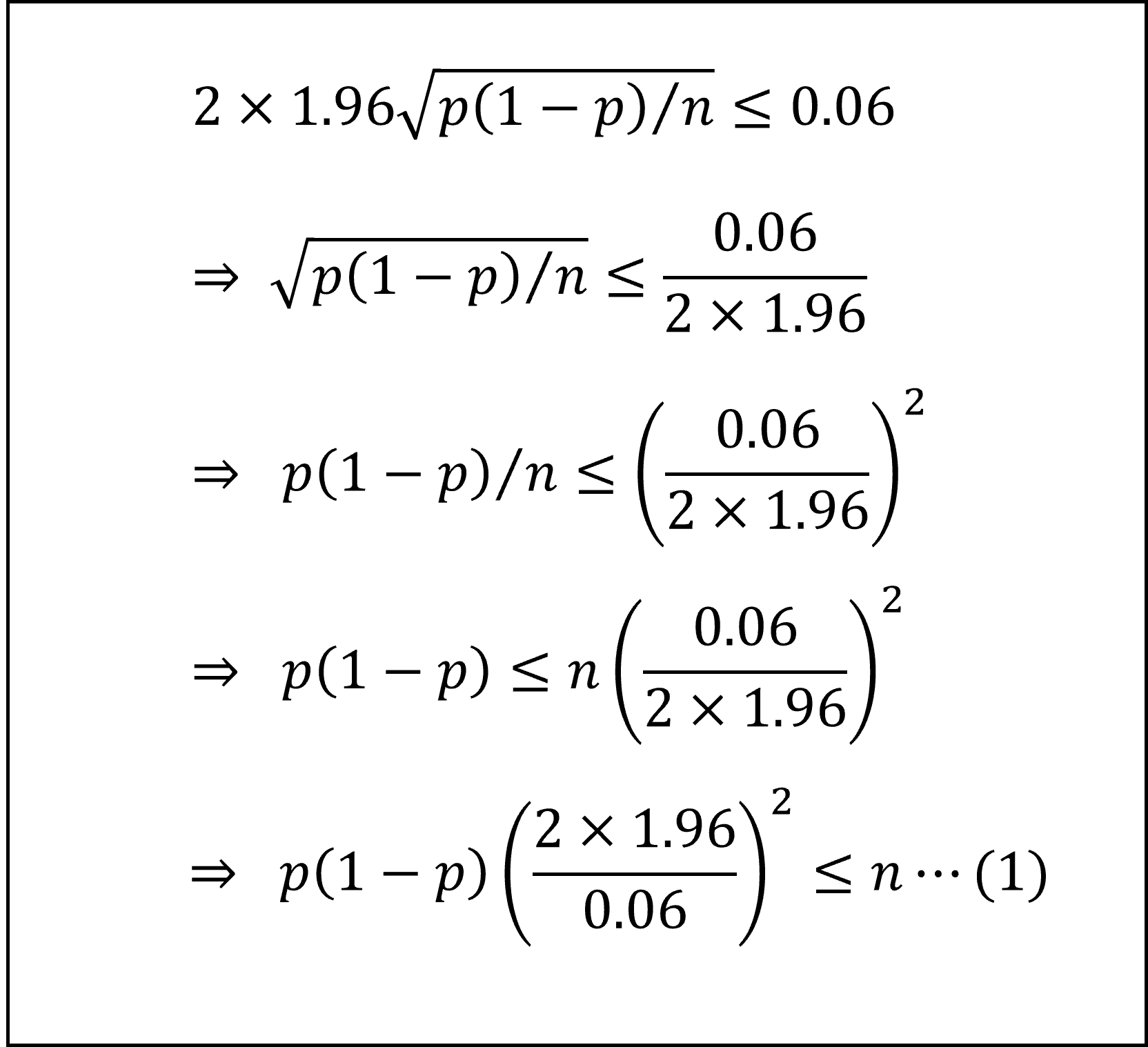
となります。ここで、政策の支持率pについての事前情報がないことから、安全のためp(1-p)が最大となるp=1/2のときを考えると
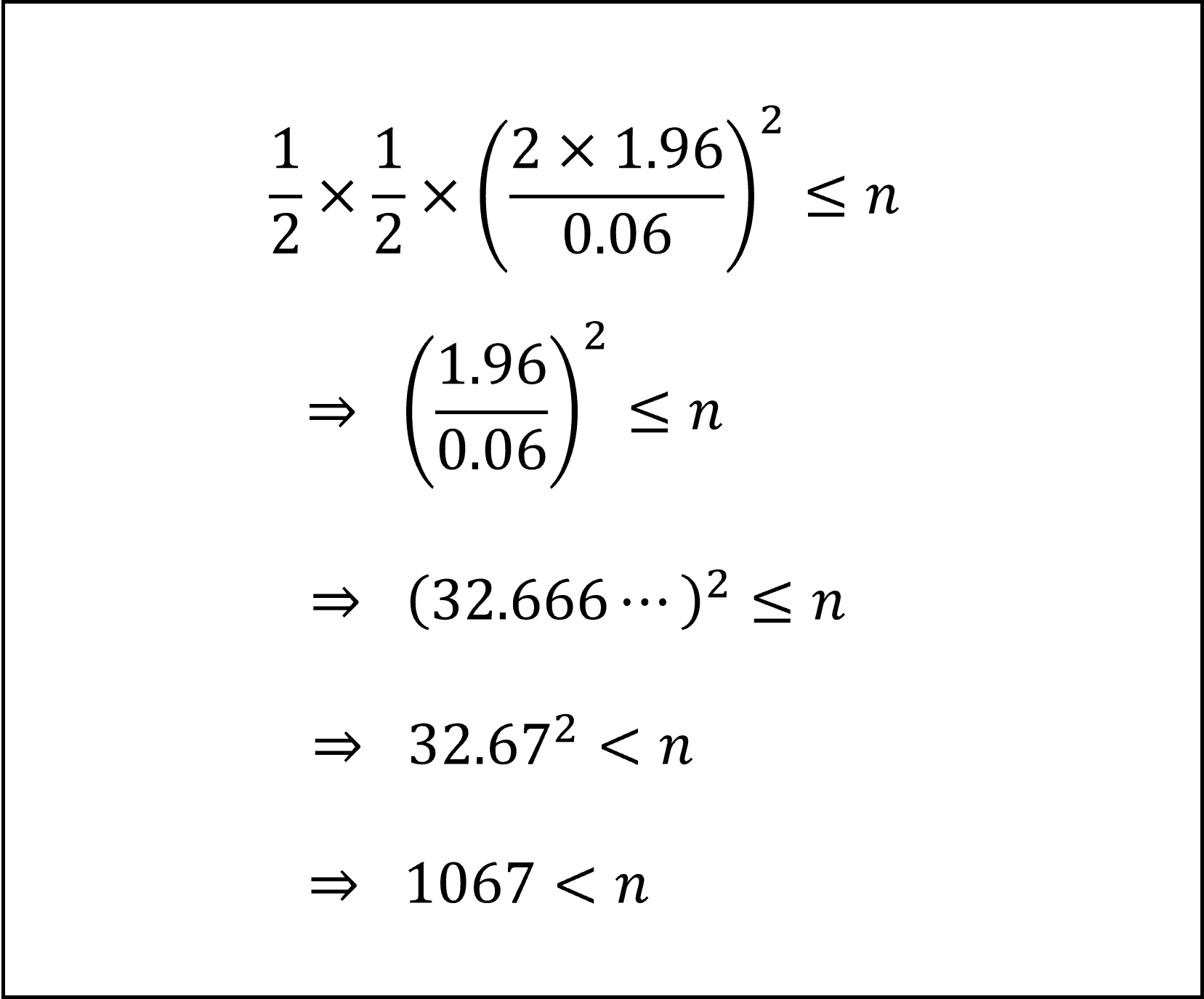
となります。したがって、標本の大きさ n は少なくとも(およそ)1067人以上必要になります。
[26番]およそp=0.8ということが分かっているので、[25]で整理した(1)式にp=0.8=4/5を代入して以下のように不等式を整理できます。
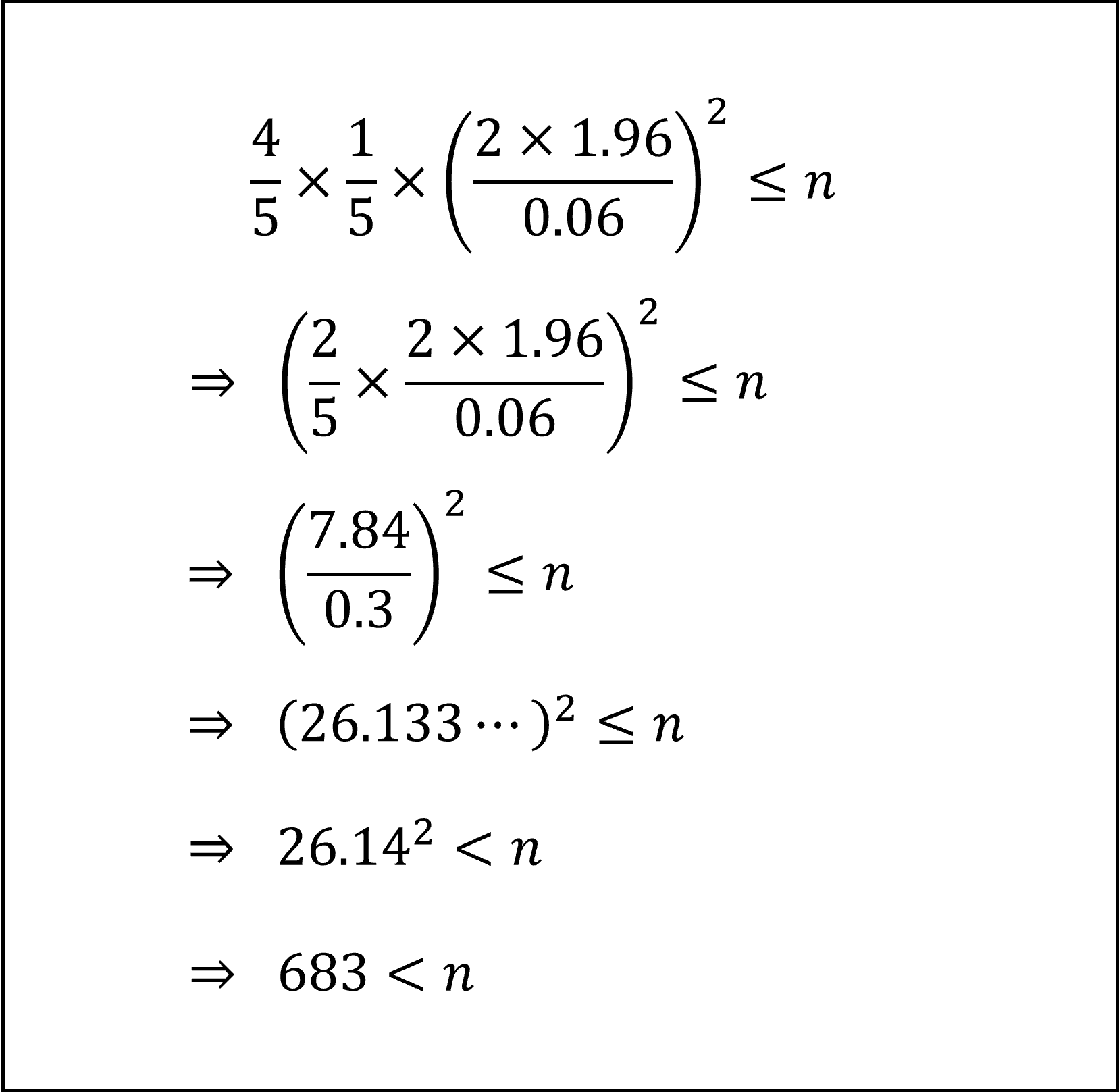
したがって、標本の大きさ n は少なくとも(およそ)684人以上必要になります。
補足
- 母比率の区間推定の問題では多くの場合、サンプルサイズ n が決まっていて標本調査の結果(標本比率)から信頼区間を求める流れです。
- それに対して、今回の問題は調査前にサンプルサイズを設計したいという状況設定であることに注意しましょう。
- 普段何気なく平方根のなかの母比率pを標本比率で代用して計算(近似計算法)しがちですが、そこに注意深くありたいですね…という出題者のメッセージを感じます。
(25,26番、以上)
問16 [27,28,29番](2019年11月試験)
テーマ
- 母平均の仮説検定
- t分布
- 自由度
正答
[27番]選択肢⑤ [28番]選択肢④ [29番]選択肢⑤
解答例
[27番]母集団分布が母平均μ、母分散σ^2の正規分布であることから
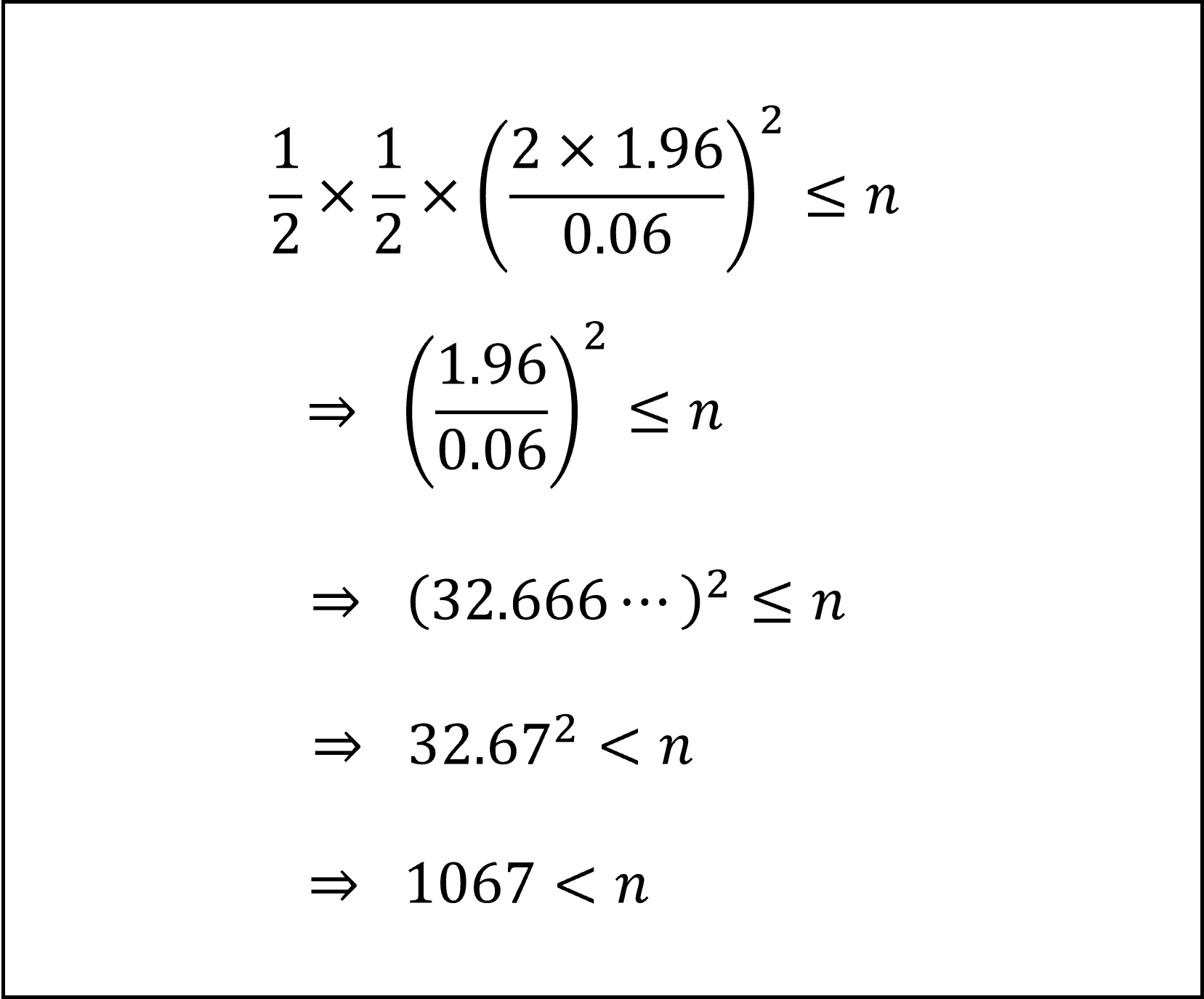
となります(母分散に不偏分散を代用していることから自由度は16-1=15となります)。
[28番]帰無仮説は「体重が減少しない:”前-後”の母平均 μ =0」で、対立仮説は「体重が減少する:”前-後”の母平均 μ >0」となりますので、選択肢④が正答になります。
[29番]t分布の付表より自由度15のt分布における上側5%点は1.753ですので
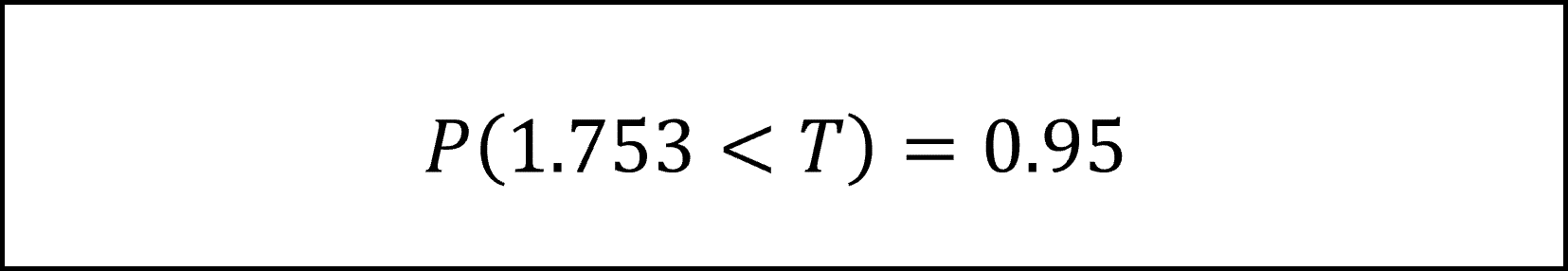
となります。したがって、棄却域は1.753より大きい領域となります。
検定統計量の実現値は
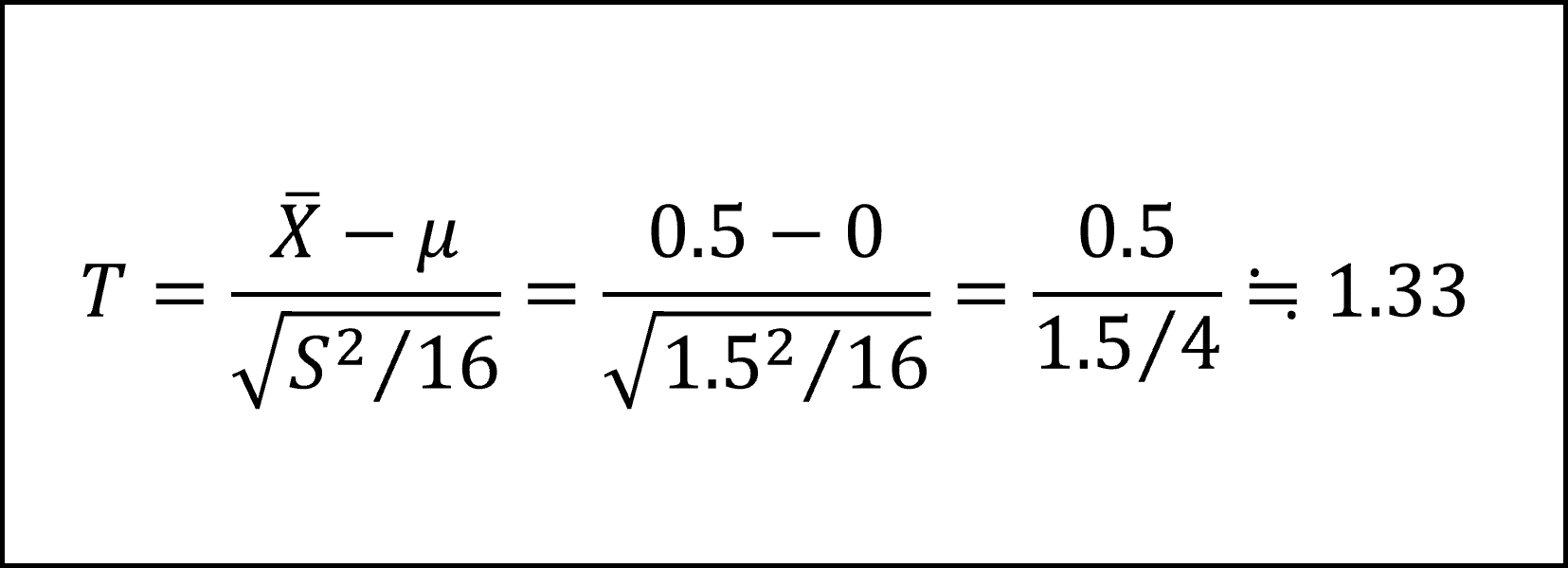
となり棄却域に入りませんので、帰無仮説は棄却されず、対立仮説が正しい(体重が減少する)とは判断できません。
補足
- 対応のある母平均の差の仮説検定は、前後の差を1つの標本とみなして1標本問題に読み替えて検定を行います。
(27,28,29番、以上)
問17 [30,31,32番](2019年11月試験)
ポイント
- 一元配置分散分析
- 全体平方和
- 水準間平方和
- 残差平方和
- 自由度
- F検定
- F分布の付表
正答
[30番]選択肢① [31番]選択肢③ [32番]選択肢③
解答例
[30番] 月ごとの売上高の差を分析する一元配置分散分析ですので、「月」が変動要因となり、「1月、2月、…、12月」が各水準となります。
水準間平方和は各水準の平均(月別平均)が全体平均からどのくらい変動しているかを表すもので、具体的には以下の式になります(データの数が11年分ありますので「×11」をします)。
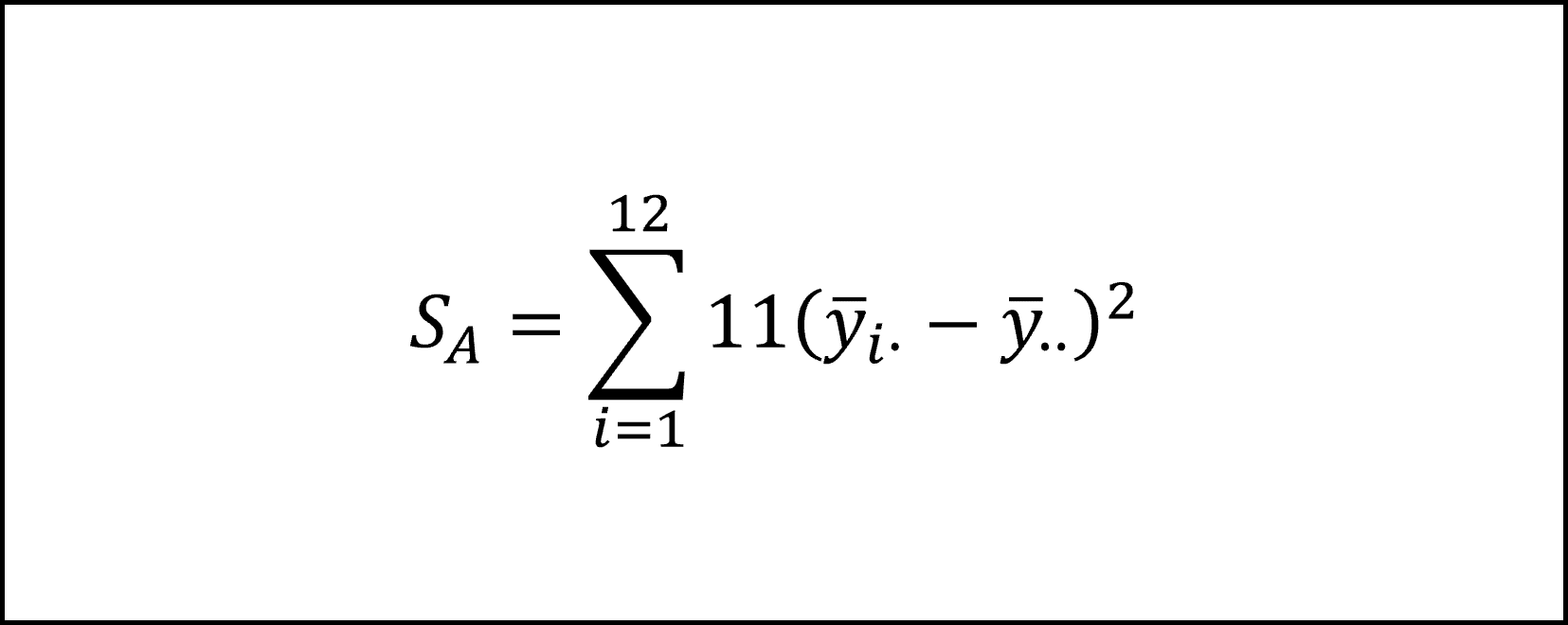
また、残差平方和は水準内平方和とも呼ばれ、各水準内における各観測値(各月の年別の個々の値)が各水準平均(各々の月別平均)からどれくらい変動しているかを表します。具体的には以下の式になります。
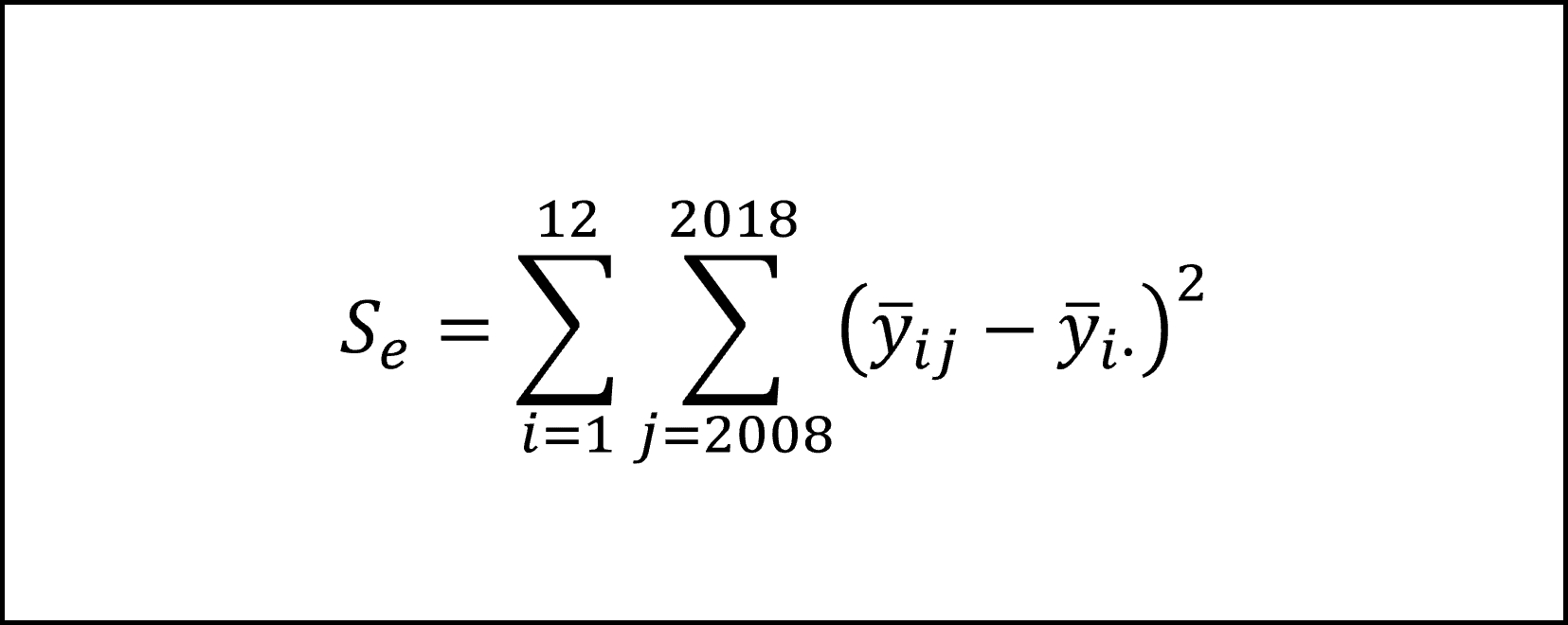
[31番] 水準間平方和の自由度は水準数aから1を引いた値になりますので、12-1=11となります。
残差平方和(水準内平方和)の自由度は観測データ数nから水準数aを引いた値になりますので、(11×12)-12=120となります。
なお、全体平方和の自由度は n-1=(11×12)-1=131となり、これは水準間平方和の自由度と残差平方和の自由度の和と等しくなります。
[32番] 《記述Ⅰ》一元配置分散分析では帰無仮説を「各水準の母平均μiがすべて等しい」とし、対立仮説を「各水準の母平均μiのうち少なくとも1つが異なる」として検定を行います。したがって対立仮説を「各水準の母平均μiのすべてが異なる」とした記述Ⅰの内容は「誤り」です。
《記述Ⅱ》検定統計量Fの実現値(F-値)は問題文より3.0471で、このF-値は自由度(11,120)のF分布にしたがいます。
自由度(11,120)のF分布の上側5%点は、付表から以下の不等式の範囲にあることがわかります。
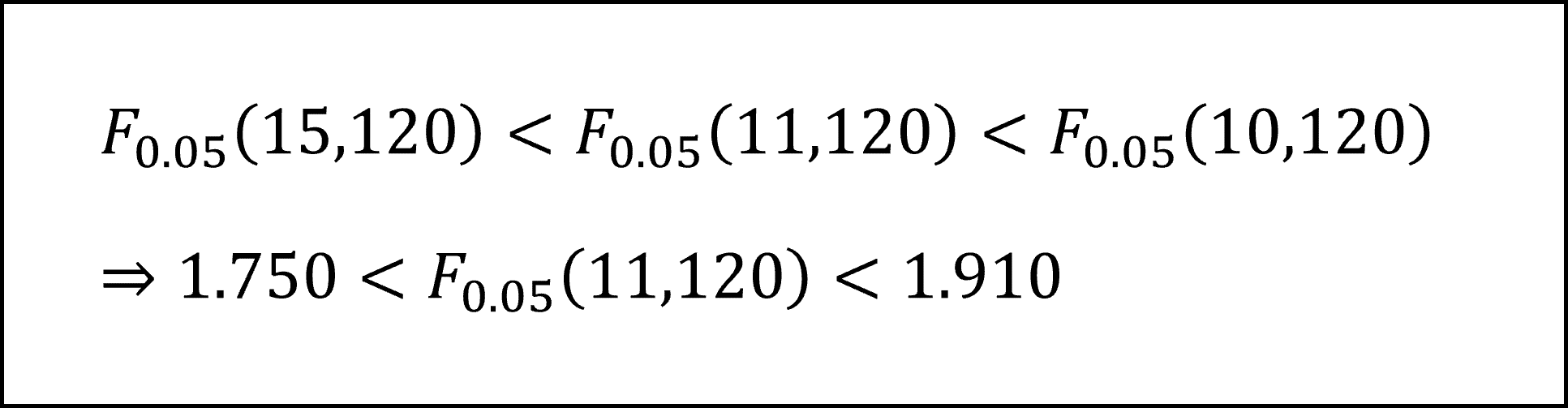
F-値3.0471は上記の範囲にある上側5%点よりも大きくなっていますので、棄却域に入ります。したがって帰無仮説は棄却されるため、「差があると判断できない(帰無仮説が棄却されない)」とする記述Ⅱの内容は「誤り」です。
《記述Ⅲ》自由度(11,120)のF分布における上側2.5%点は、付表から以下の不等式の範囲にあることがわかります。
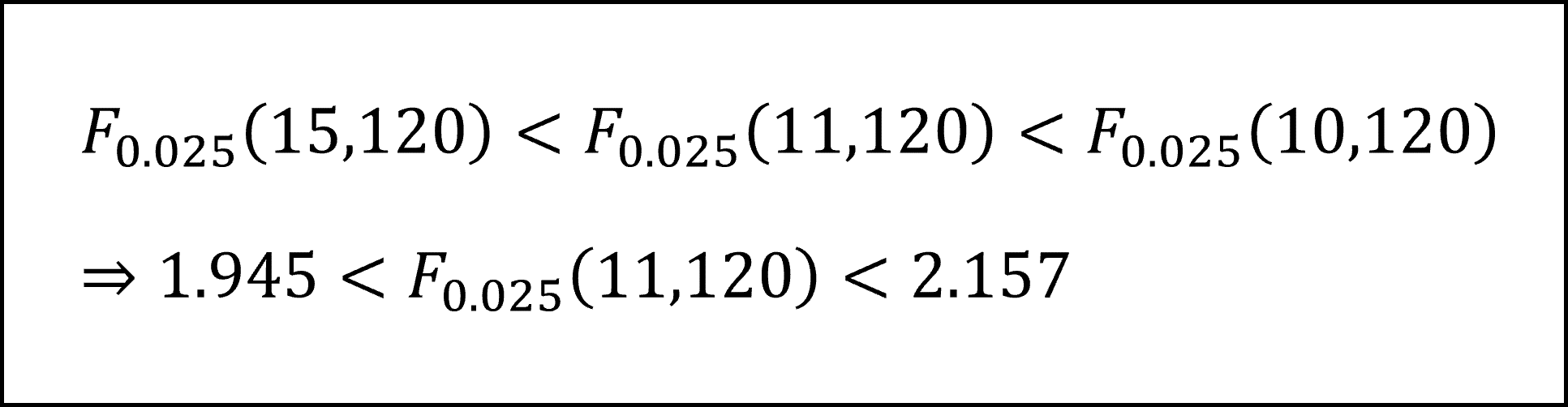
検定統計量Fの実現値(F-値)3.0471は、上記の上側2.5%点よりも大きくなっていますので、P-値(すなわち3.0471≤Fとなる確率)は2.5%よりも小さくなります。よって記述Ⅲの内容は「正しい」です。
補足
- 一元配置分散分析の主役は「水準(カテゴリ)」です。
- 本問では「各月(1月、2月、…、12月)」が水準であって、「各年(2008年、2009年、…、2018年)」が水準ではないことに注意しましょう。
(30,31,32番、以上)
問18 [33,34,35番](2019年11月試験)
テーマ
- 重回帰モデル
- 偏回帰係数の解釈
- モデルの解釈
正答
[33番]選択肢① [34番]選択肢⑤ [35番]選択肢③
解答例
[33番] 偏回帰係数は、他の説明変数を一定としたときに、その説明変数が1単位増加すると被説明変数がどれだけ変動する傾向があるかを表します。したがって記述Ⅰが「正しい」内容になります。
[34番] 《記述Ⅰ》予測値の平均と観測値yの平均は等しくなりますので「正しい」です。
《記述Ⅱ》最小二乗法により推定された回帰式は必ず(x平均, y平均)を通ります。推定された以下の回帰式にx=41.0を代入すると

となりますので、x=41.0はxの平均であることが確認できます。よって「正しい」内容になります。
《記述Ⅲ》「残差=観測値y-予測値」ですので、予測値に残差を加えると観測値(元のデータ)yとなります。よって「正しい」です。
[35番] 《記述Ⅰ》重回帰モデルの定期収入と賞与の係数が等しいとき、

となり、世帯主収入合計を説明変数とする単回帰モデルが得られますので「正しい」です。
《記述Ⅱ》重回帰モデルの自由度調整済み決定係数は0.5161であるのに対して単回帰モデルの自由度調整済み決定係数は0.5261で、前者が後者より小さくなっています。よって「誤り」です。
《記述Ⅲ》「正しい」内容です。
補足
- 重回帰モデルは複数の説明変数を含み、ある説明変数が変動したら、別の説明変数も変動すること(つまり説明変数間の相関)が組み込まれたモデルになります。
- したがって偏回帰係数の解釈として「その説明変数が増加したときに被説明変数がどれだけ変動するかを表す」では言葉足らずで、必ず、「他の説明変数を一定としたとき」とか「他の説明変数を固定したとき」という条件をつけて解釈します。
(33,34,35番、以上)

