
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問11 [20番](2019年6月試験)
テーマ
- 標準化
- 標準正規分布
- 上側確率/下側確率
正答
選択肢⑤
解答例
確率変数Xが期待値2、分散9の正規分布N(2, 9)にしたがいますので、これを標準化すると以下のように整理できます。
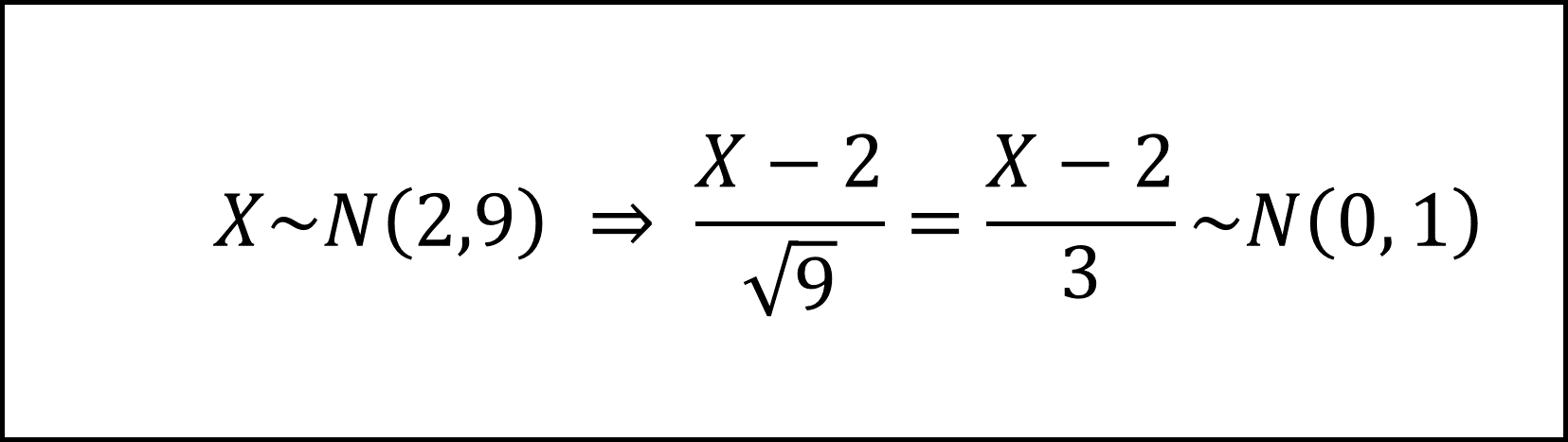
これを踏まえ、求めたい確率を以下のように整理します。
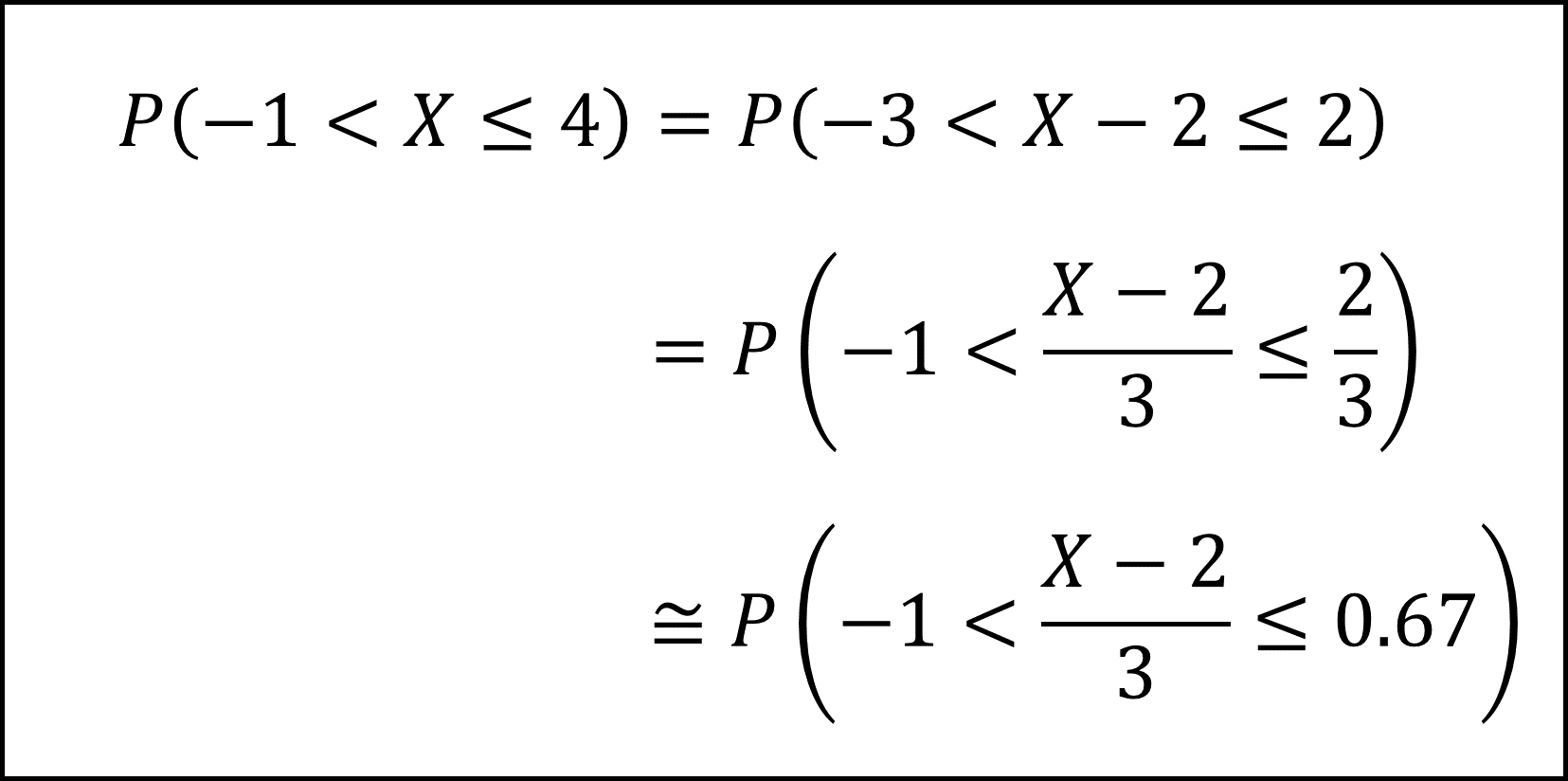
標準正規分布の付表では「正の値についての上側確率(その値よりも大きい値をとる確率)」を確認できますので、以下のように「正の値についての上側確率」の式に整理します。
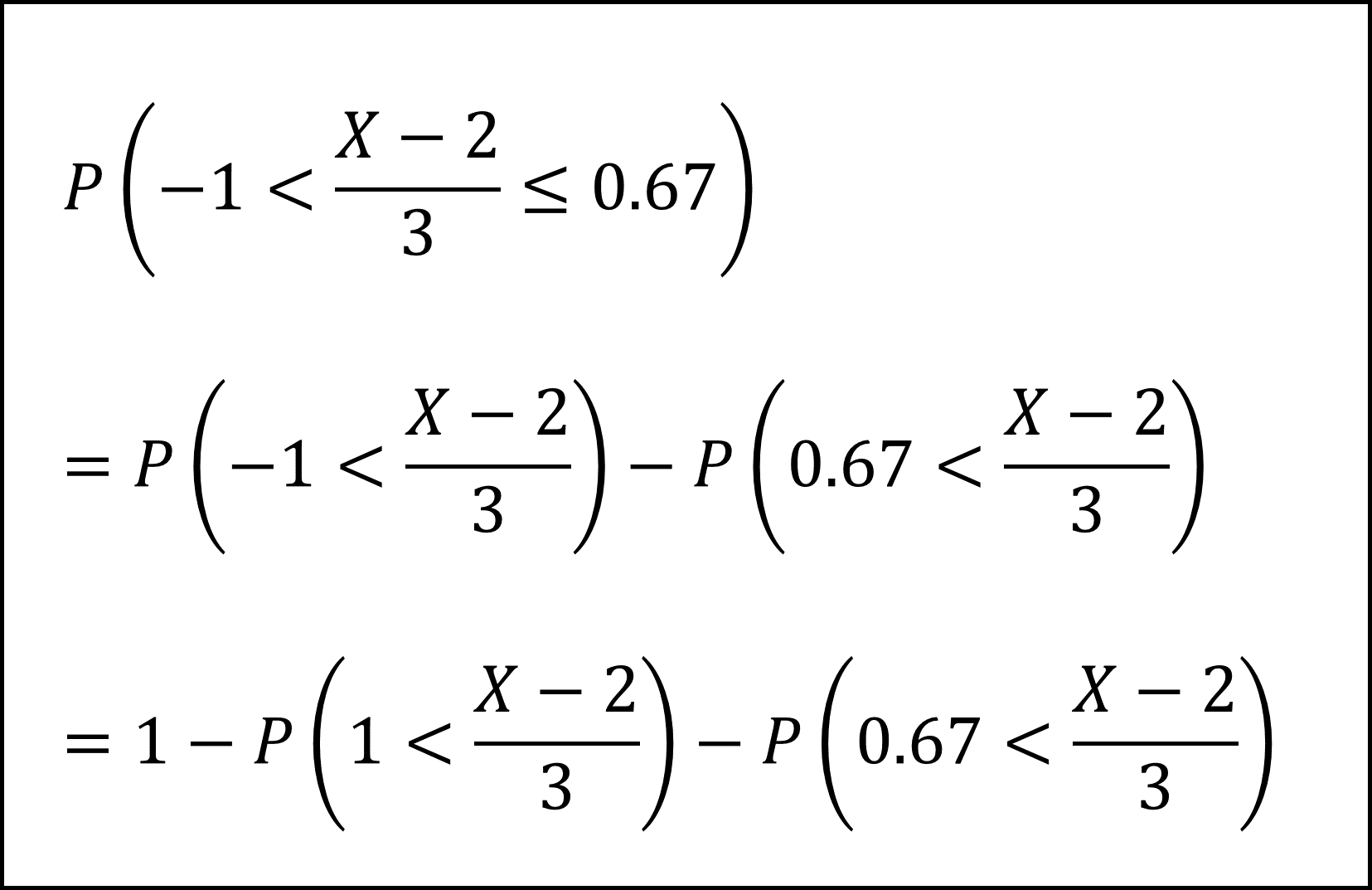
標準正規分布の付表から上側確率を確認して
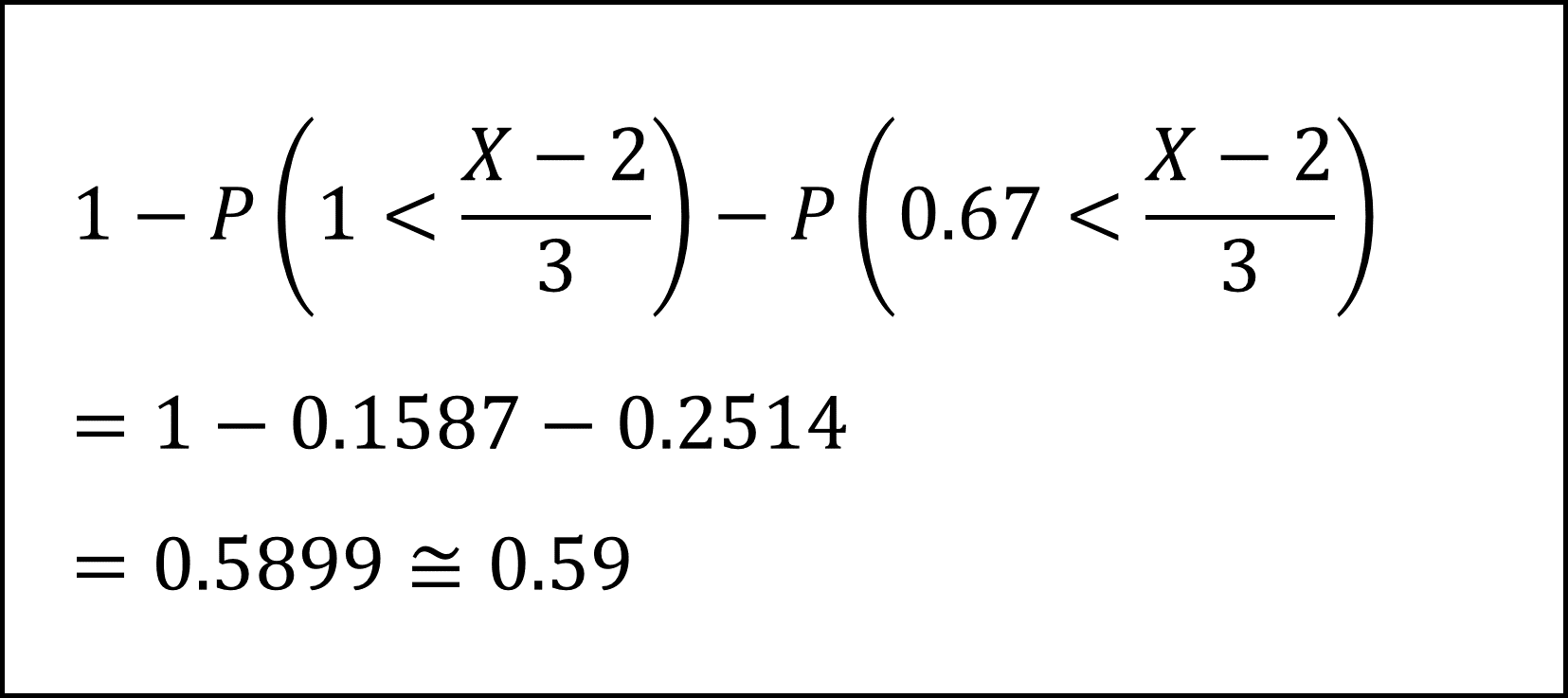
となります。
補足
- 上側確率(その値よりも大きい値をとる確率)と下側確率(その値よりも小さい値をとる確率)を混同しないように気をつけましょう。
問12 [21番](2019年6月試験)
テーマ
- 標本平均
- 標本平均の期待値
- 標本平均の分散
正答
選択肢④
解答例
正規母集団とありますので、以下のように分布を整理できます(標本平均の性質より、標本平均の期待値は元の分布の期待値に等しく、また、標本平均の分散は元の分布の分散をサンプルサイズnで割った値となります)。
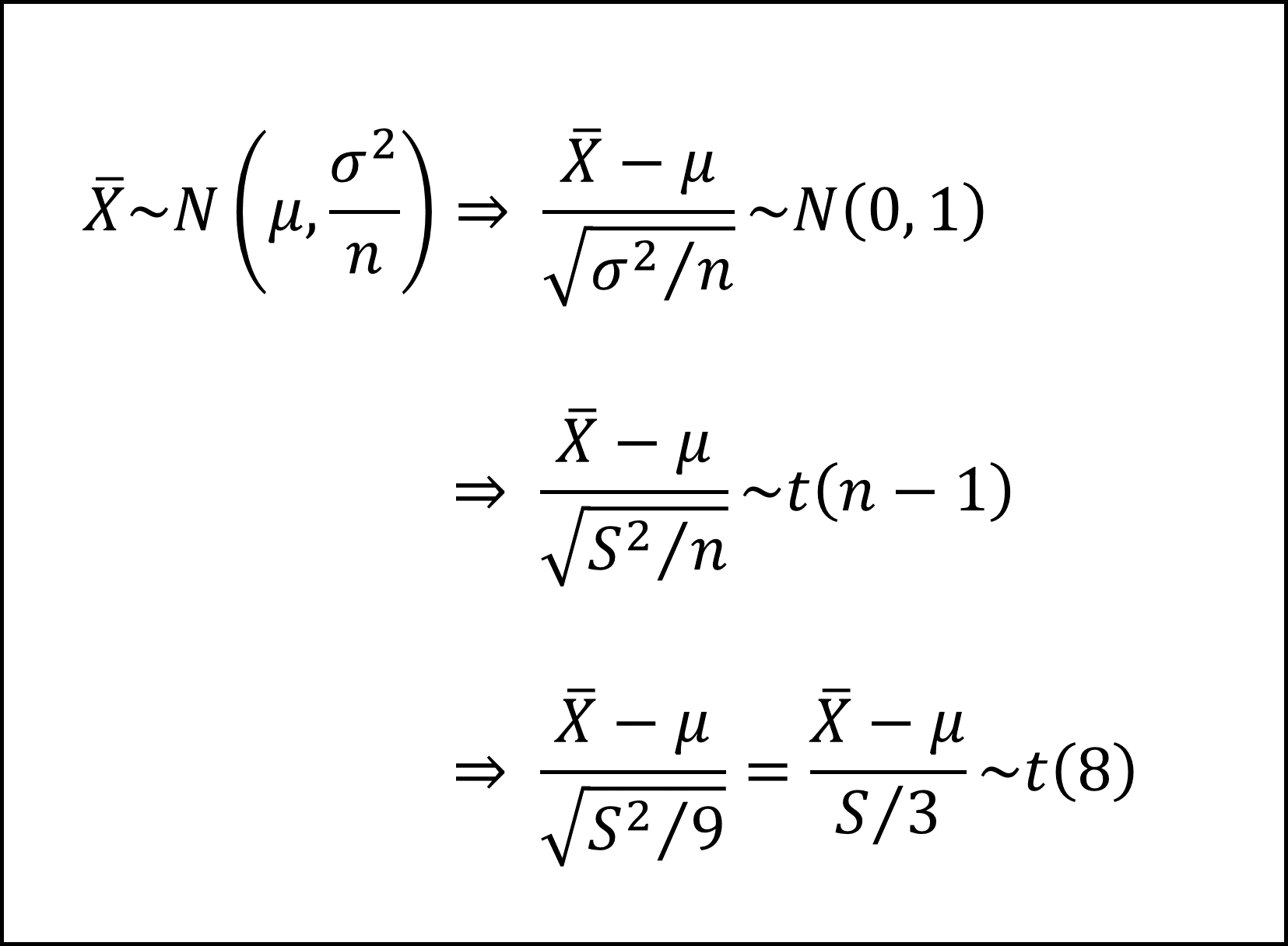
※母分散σ^2を不偏分散S^2で代用しているため、標準正規分布ではなく自由度n-1のt分布にしたがいます。
これを踏まえ、求めたい確率を以下のように整理します。
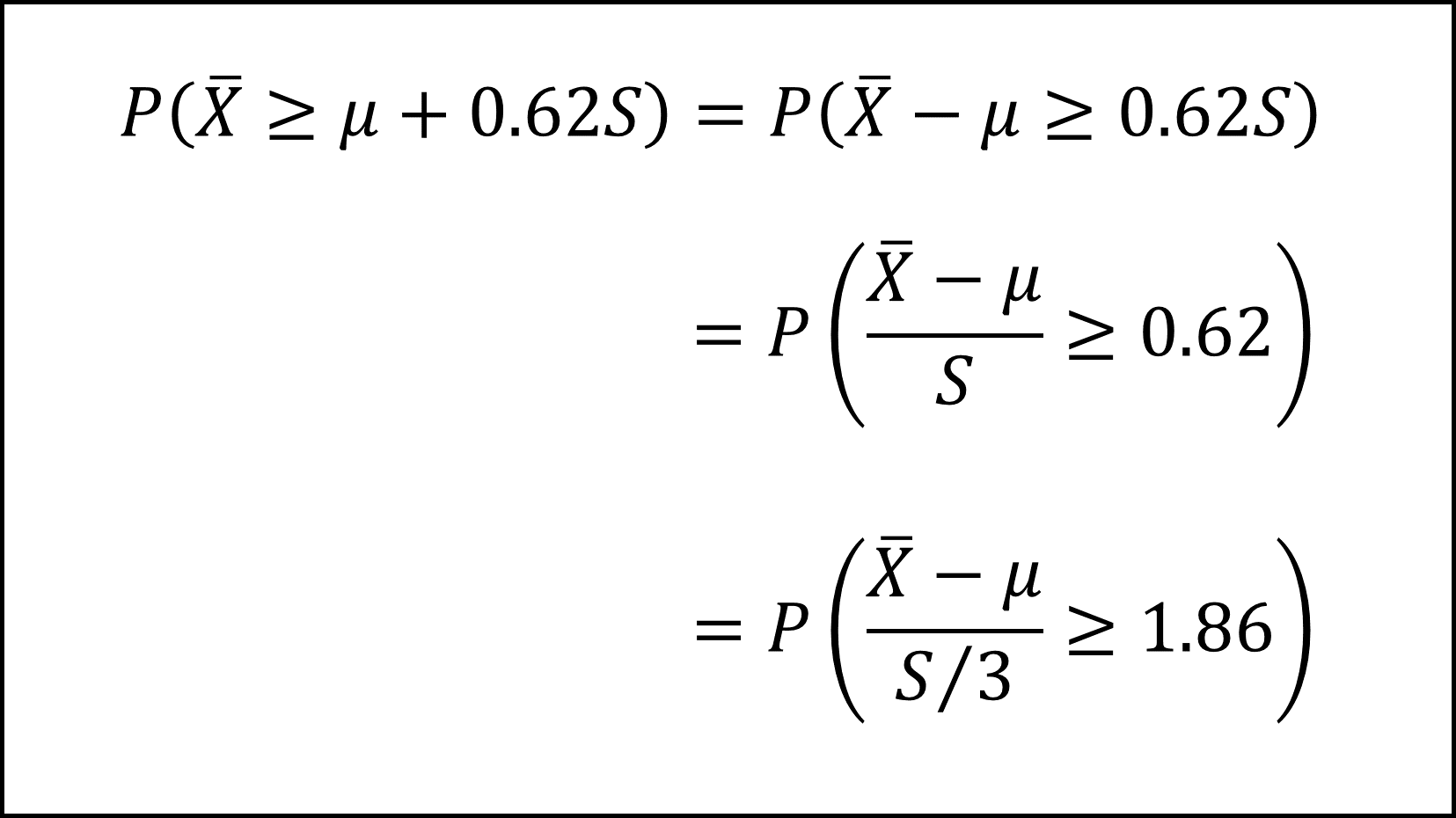
ここでt分布の付表より自由度8のt分布における上側5%点が1.86であることから
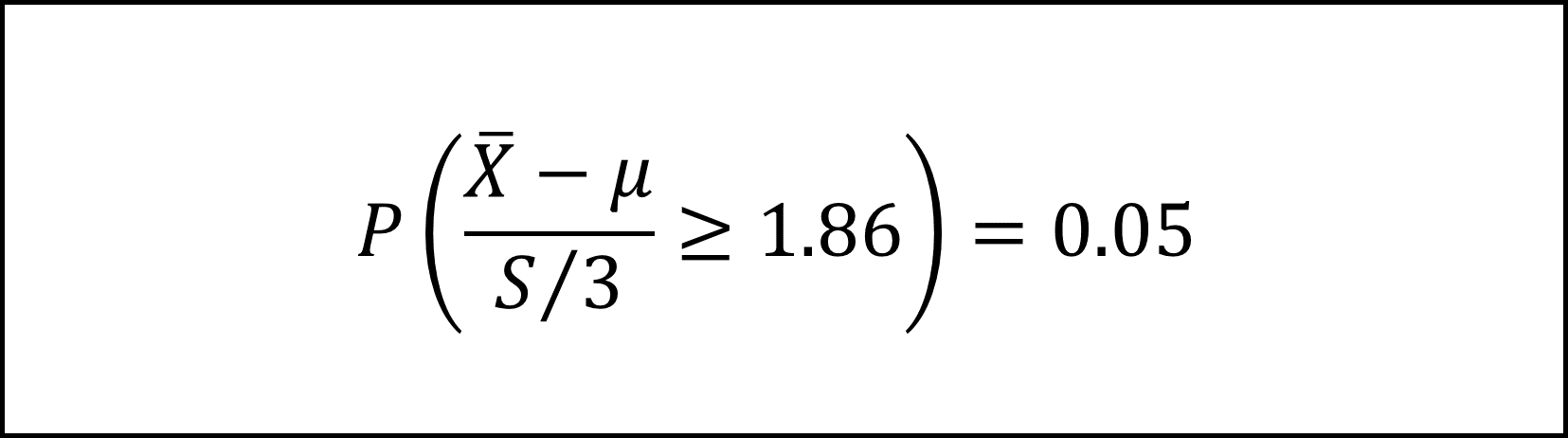
となります。
補足
- 式を整理するプロセスでミスをしてしまいそうな問題です。
- 短い問題文で多くの論点を盛り込んだ良問であると思います。
問13 [22,23,24番](2019年6月試験)
テーマ
- 事象と確率
- 中央値
- 最頻値
- 期待値
正答
[22番]選択肢④ [23番]選択肢③ [24番]選択肢⑤
解答例
[22番] p3は標本平均が3となる確率で、すなわち、X1+X2=6となる確率です。
X1+X2=6となるX1, X2の組み合わせは、(X1, X2)={(2, 4),(4, 2)}の2通りです。全体の組み合わせの数は16通りですので、p3=2/16=1/8となります。
P6は標本平均が6となる確率で、すなわち、X1+X2=12となる確率です。
X1+X2=12となるX1, X2の組み合わせは、(X1, X2)={(4, 8),(6, 6),(8,4)}の3通りです。全体の組み合わせの数は16ですので、p6=3/16となります。
[23番] X1, X2の組み合わせ16通りを、標本平均の値別に整理すると以下のようになります。
- ・標本平均が2 → 【1通り】(2,2)
- ・標本平均が3 → 【2通り】(2,4),(4,2)
- ・標本平均が4 → 【3通り】(2,6),(4,4),(6,2)
- ・標本平均が5 → 【4通り】(2,8),(4,6),(6,4),(8,2)
- ・標本平均が6 → 【3通り】(4,8),(6,6),(8,4)
- ・標本平均が7 → 【2通り】(6,8),(8,6)
- ・標本平均が8 → 【1通り】(8,8)
以上より、標本平均の中央値は5で、標本平均の最頻値も5であることが分かります。
[24番] 《選択肢①》標本平均の期待値は母集団の期待値に一致しますので、その母集団から抽出された標本が1つ(X1かX2のどちらかが)あれば計算できます(なお、標本平均の期待値は5です)。
《選択肢②》標本平均の期待値の厳密な値を計算することができます。具体的には以下の式で計算できます。
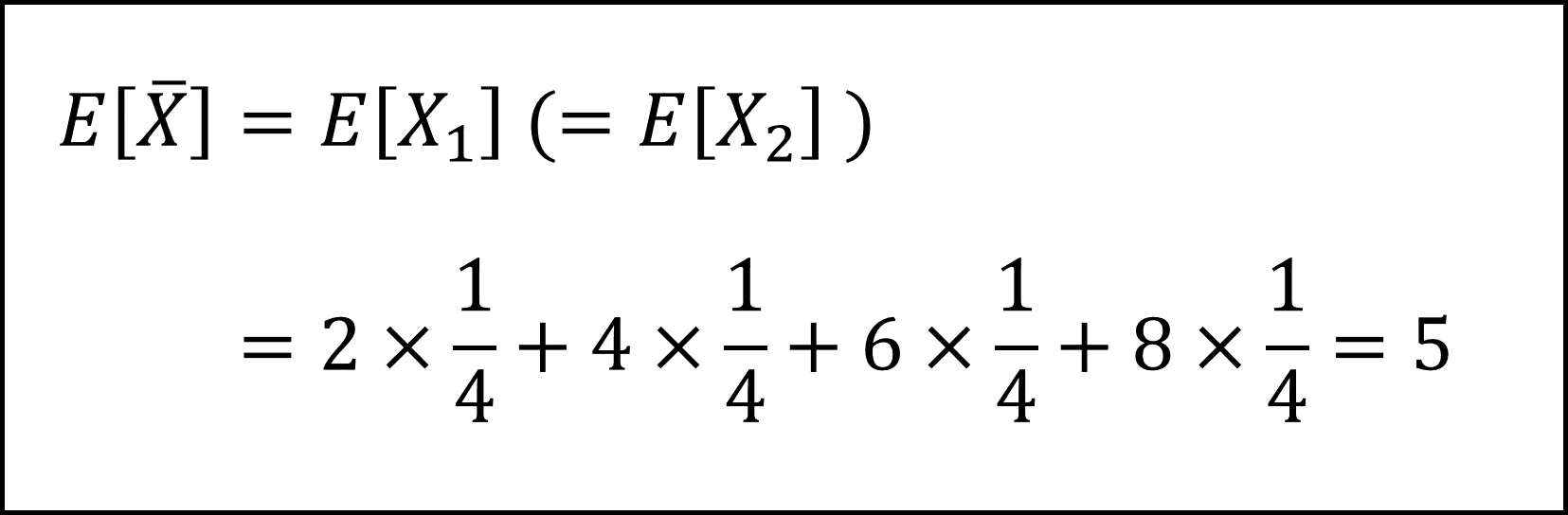
《選択肢③》標本平均は母平均の「不偏推定量」で、その根拠は、標本平均の期待値が母平均に等しいことです。したがって、標本平均の期待値が母平均に等しいという表現は「誤り」です。また、標本平均の期待値が4か6というのも「誤り」で、上記で計算したように正しくは「5」です。
《選択肢④》標本平均の期待値は具体的に観測された値によって計算されるものではなく、理論上、確率的に期待される値ですので「誤り」です。
《選択肢⑤》正しい内容です。期待値は標本抽出によって観測された値によって計算されるものではなく、理論上、確率的に期待される値ですので、1つの定数値に決まります。
補足
- [23番]の組み合わせの数の整理が面倒なように感じますが、20通りくらいまでの数であれば、意外と時間を要さずに整理できます。
- 「確率変数」と「確率変数の期待値」の違いを腹落ち感をもって理解できているかが問われる問題です。期待値は、理論上、確率的に期待される値ですので、標本抽出のたびにブレるようなものではないことに注意しましょう。
問14 [25番](2019年6月試験)
テーマ
- 母比率の区間推定
- 二項分布
- 正規分布
- 中心極限定理
正答
選択肢④
解答例
目印の付いている魚の比率(母比率)を p=300/N とおきます。また、池から捕獲した魚の数をn=200、そのうち目印の付いている魚の数をxとおきます。
母集団の魚の数Nは十分に大きいことから、xは試行回数n=200、成功確率pの二項分布にしたがいます。
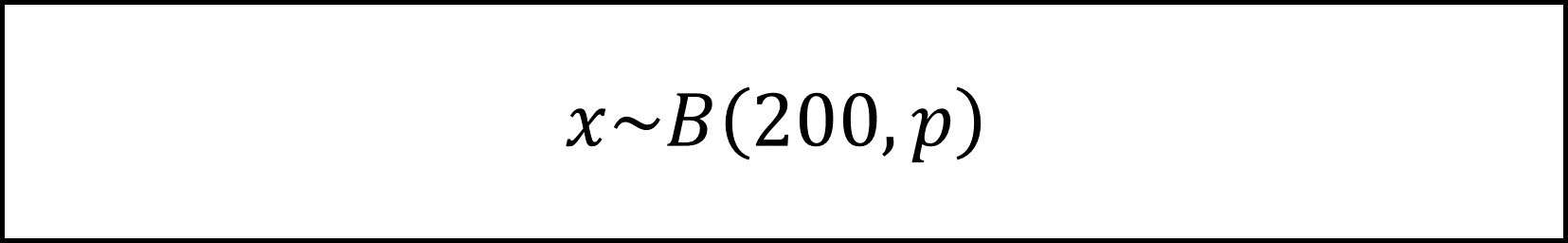
試行回数nが十分大きいことから、xは中心極限定理により正規分布にしたがいます(期待値はnp=200p、分散はnp(1-p)=200p(1-p))。
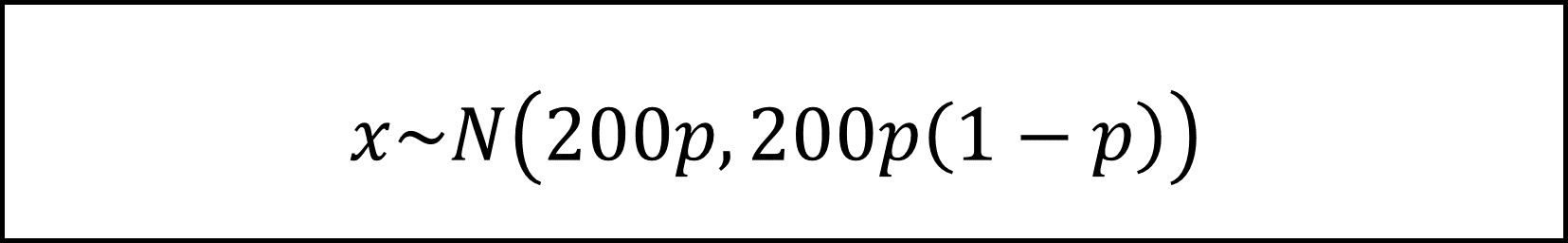
左辺を標本比率のかたちに整理して、これを標準化すると
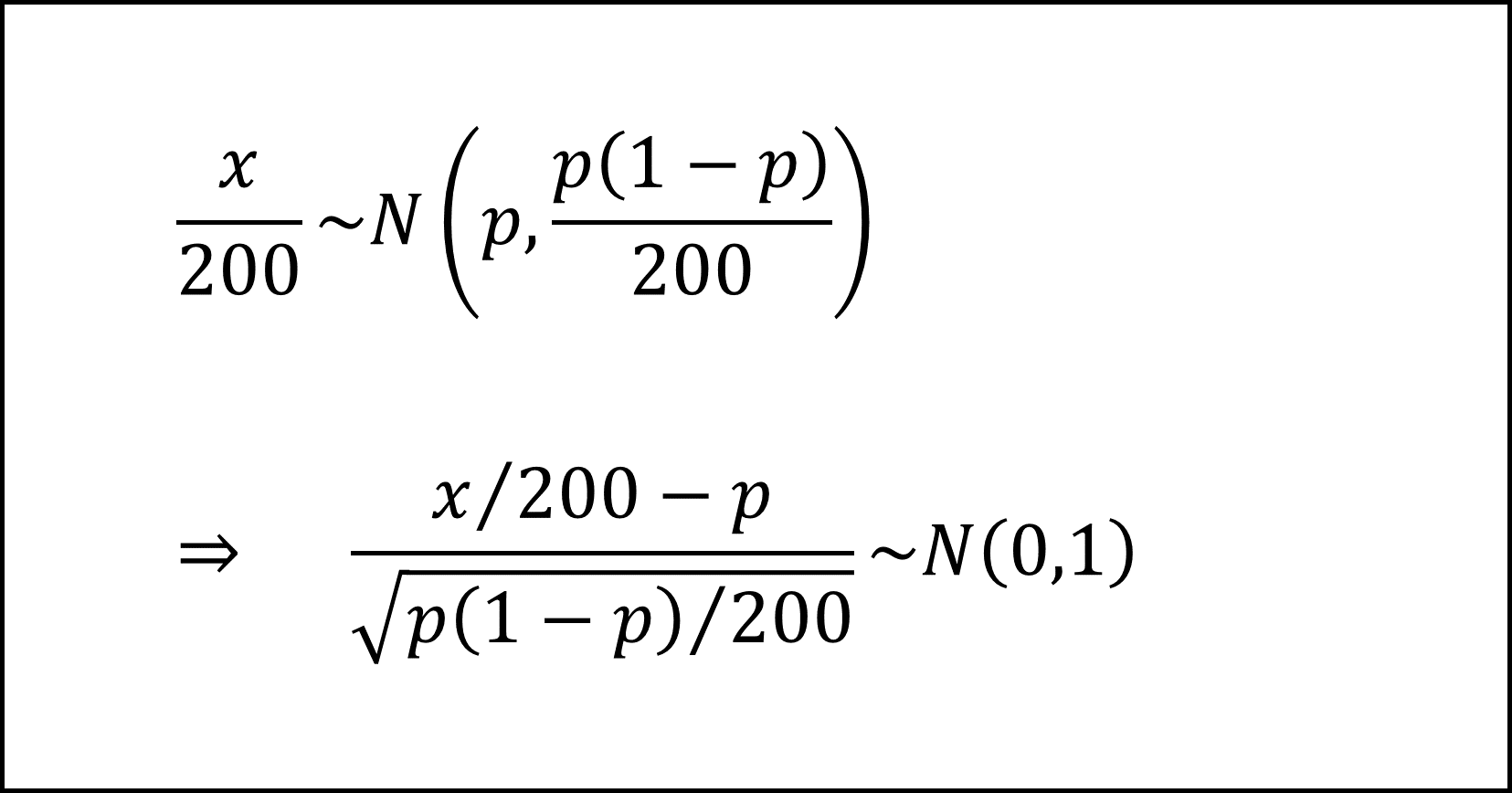
となります。
標準正規分布の付表より
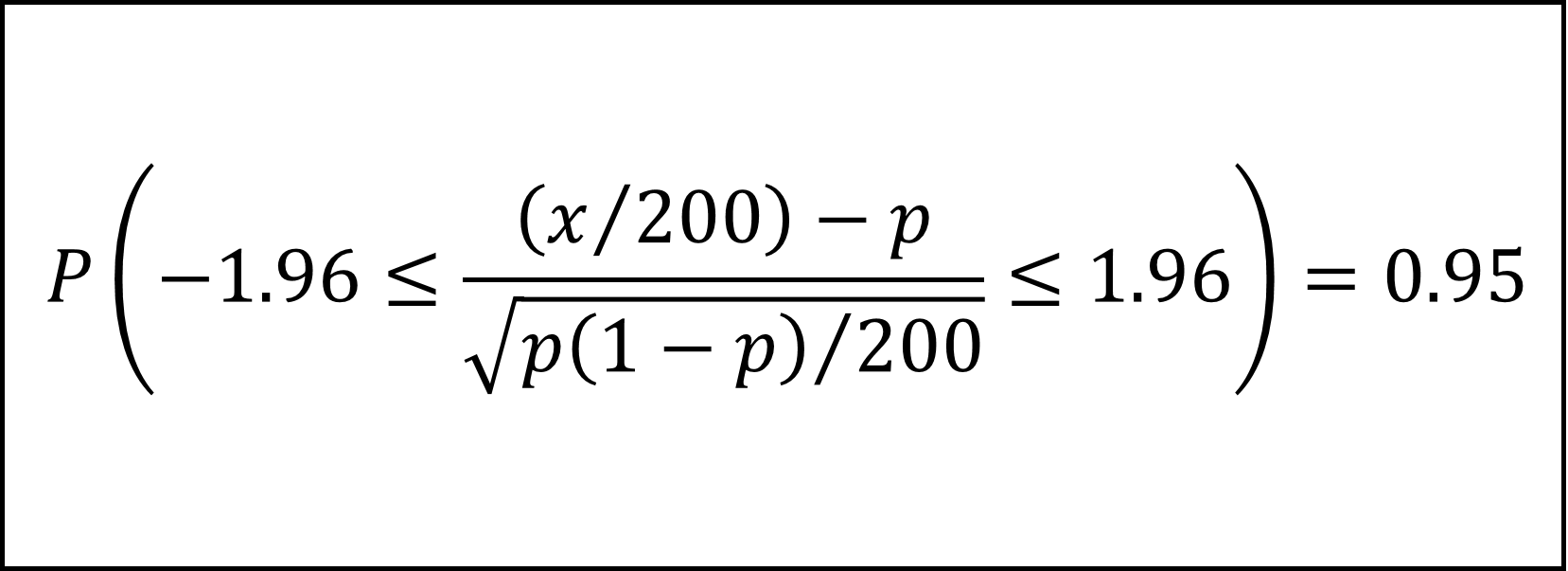
となり、x=20を代入して不等式を整理すると
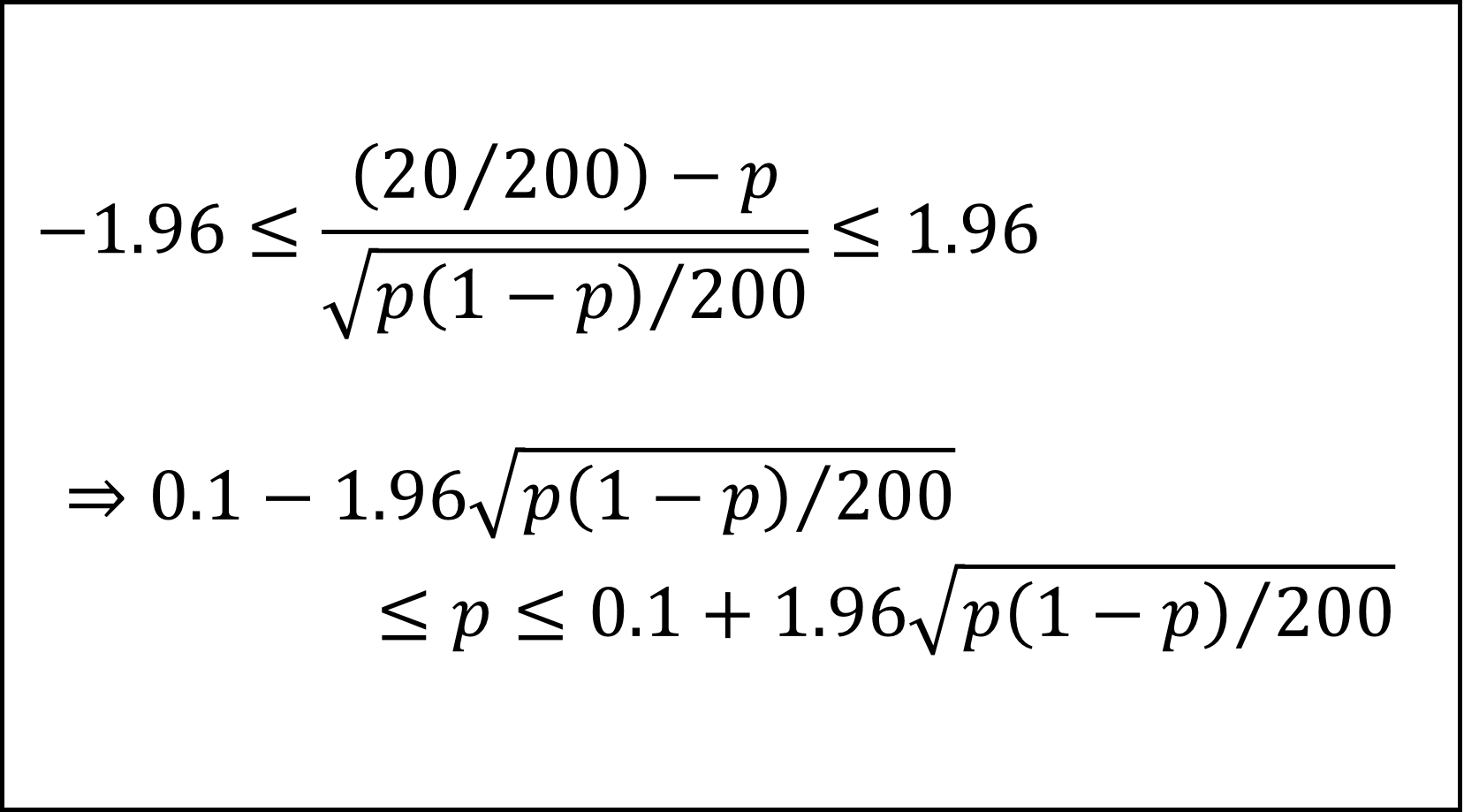
ここで、平方根のなかのpを標本比率x/n=20/200=0.1で近似的に置き換えて式を整理すると
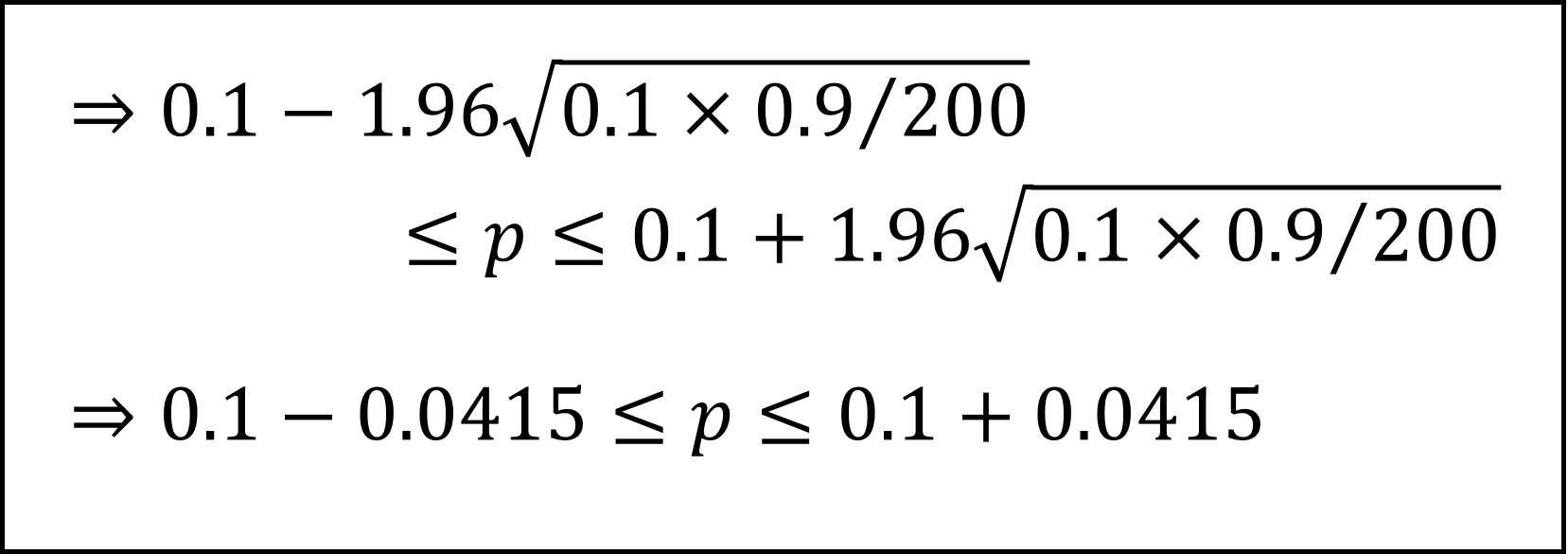
となります。
補足
- 母比率の区間推定は(毎度のことですが)計算が煩雑ですので慎重に計算しましょう。
- 母比率の区間推定は「超幾何分布の二項分布近似」「二項分布の正規分布近似」「母比率pの標本比率pによる近似計算」という「3つの近似」を用いています(詳細は別途記事にしたいと思います)。
問15 [26,27番](2019年6月試験)
テーマ
- 母平均の区間推定
- 母平均の仮説検定
正答
[26番]選択肢③ [27番]選択肢③
解答例
[26番] 株価の月次変化率が互いに独立に平均μ、分散σ^2の正規分布にしたがうという仮定ですので、標本をX、標本平均をXバーとおくと、以下のように分布を整理できます。
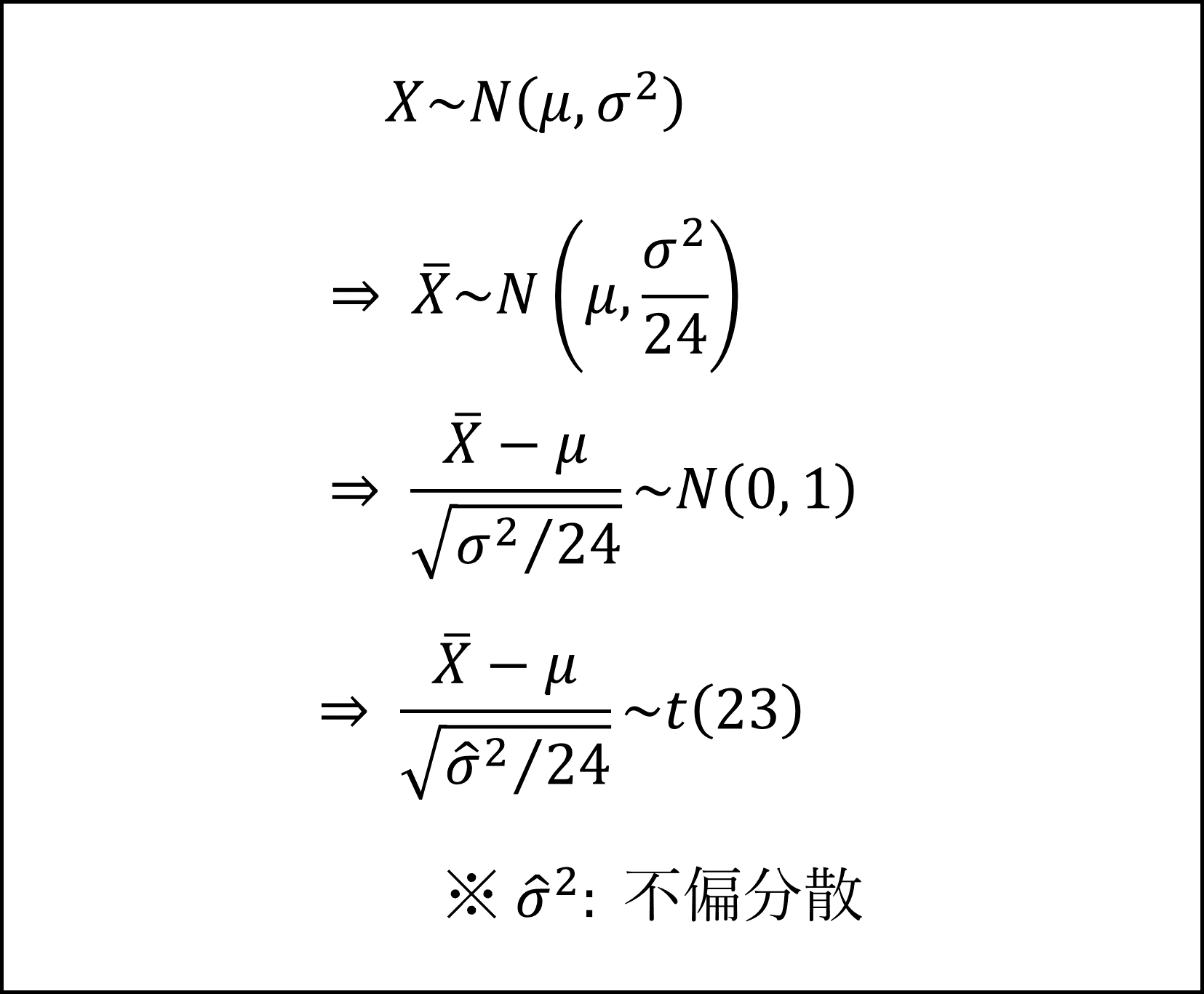
※不偏分散で代用することで標準正規分布ではなくt分布にしたがいます
ここで、t分布の付表より自由度23のt分布の上側2.5%点が2.069なので
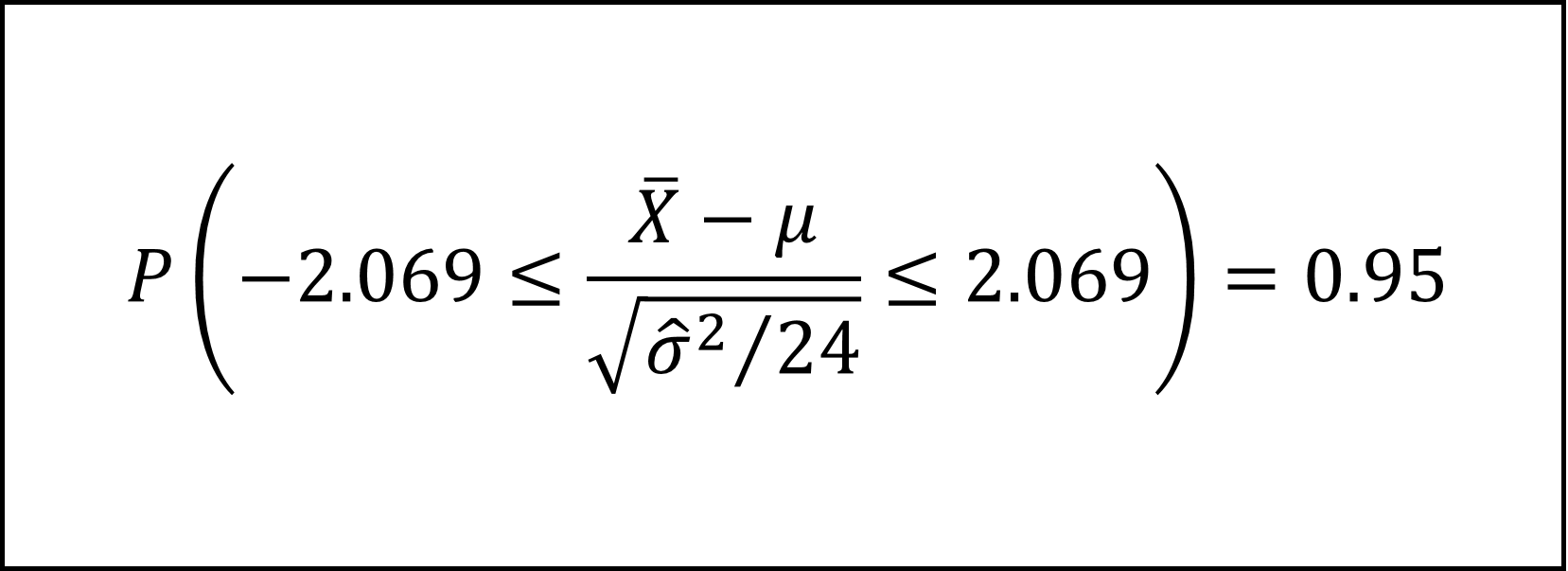
となります。この不等式を整理して、以下のように母平均μの95%信頼区間を導けます。
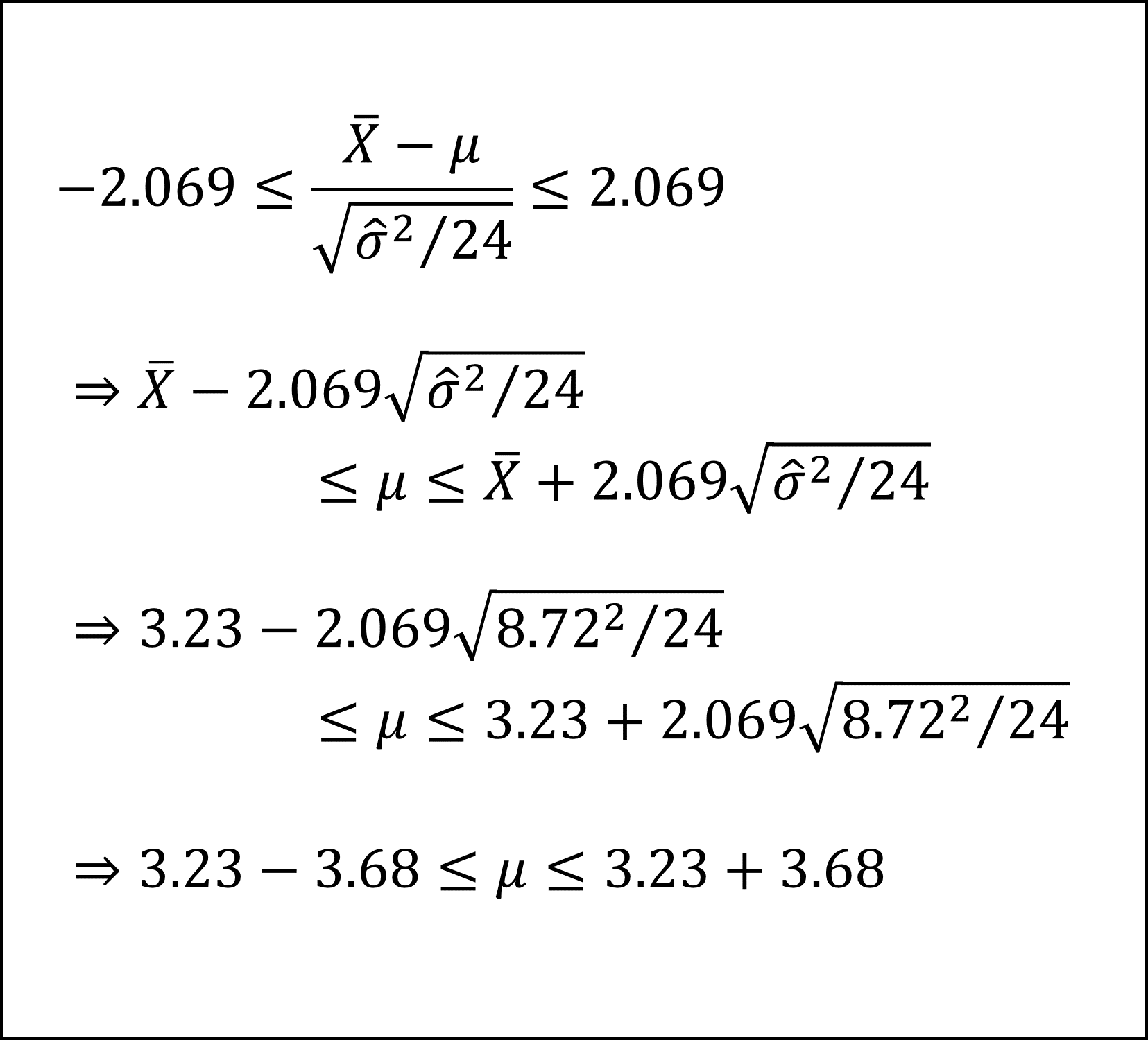
[27番] 帰無仮説が正しいとき、自由度23のt分布にしたがう値(検定統計量t)に値を代入すると、以下のようになります。
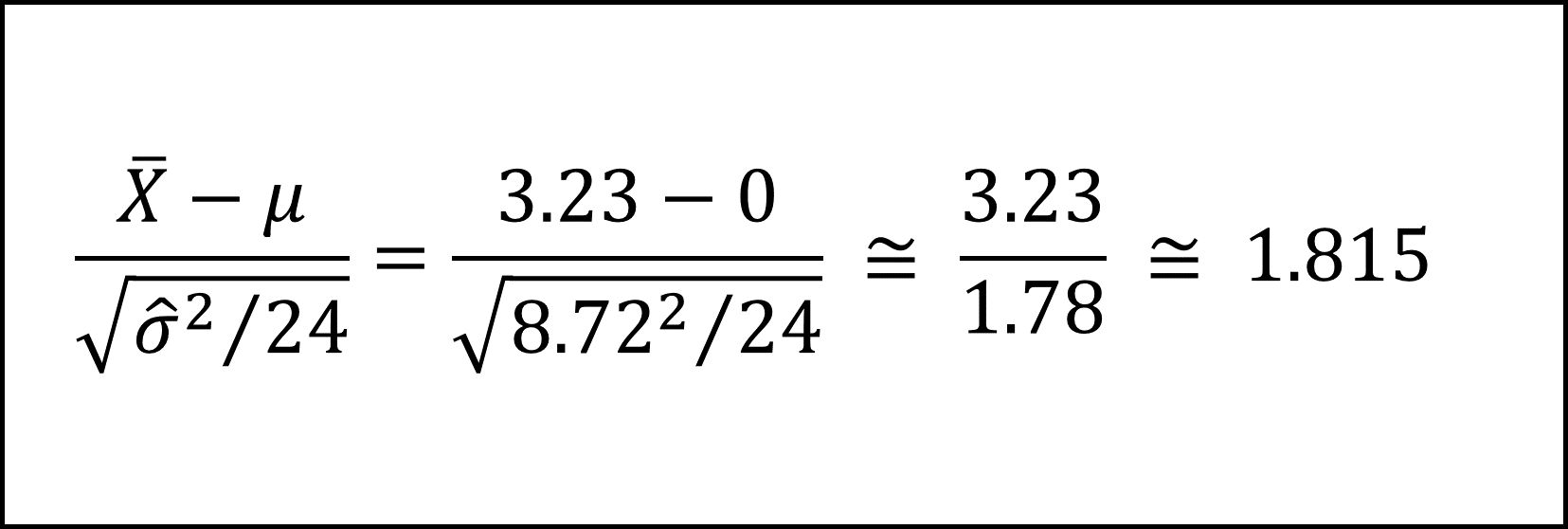
ここで、t分布の付表より、自由度23のt分布の上側5.0%点が1.714(<1.815)で、上側2.5%点が2.069(>1.815)であることから、検定統計量の実現値1.815は有意水準5%で棄却されますが、有意水準2.5%では棄却されません。
補足
- 母分散が未知ですので、不偏分散で代用し、標準席分布ではなくt分布にしたがうかたちとなることに注意しましょう。
問16 [28,29,30番](2019年6月試験)
テーマ
- 第1種の過誤
- 第2種の過誤
正答
[28番]選択肢② [29番]選択肢① [30番]選択肢②
解答例
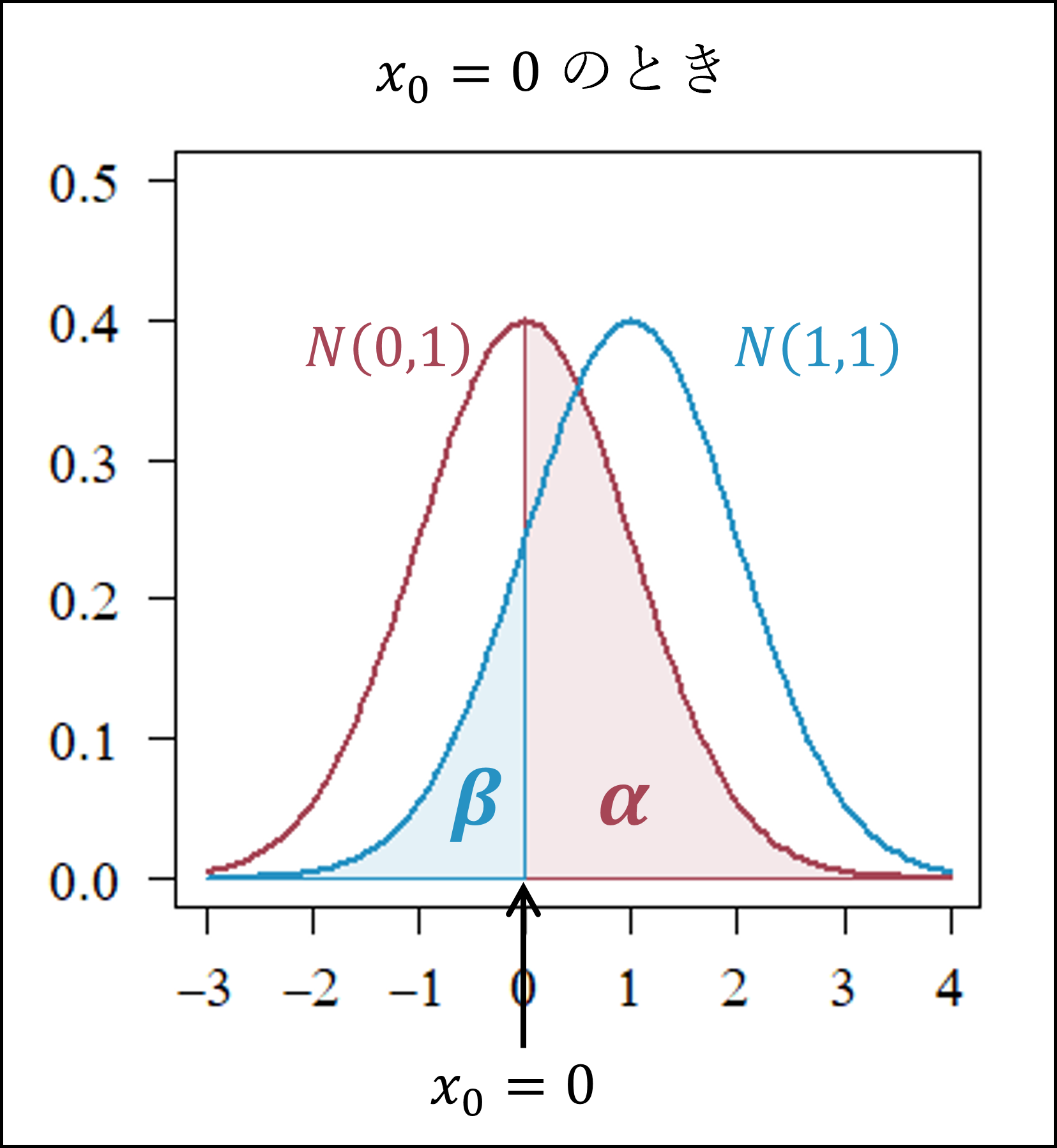
[28番] 第1種の過誤の確率αは「帰無仮説が正しいのに誤って帰無仮説を棄却してしまう誤りの確率」です。したがって、帰無仮説が正しいとき(平均θ=0のとき)にxが棄却域に入る(x≧0.8)確率を考えます。
帰無仮説が正しいとき、xは標準正規分布にしたがいますので、標準正規分布の付表よりx=0.8の上側確率を探して、具体的にはα=0.212と確認できます。
第2種の過誤の確率βは「対立仮説が正しいのに帰無仮説を棄却しない誤りの確率」です。したがって、対立仮説が正しいとき(平均θ=1のとき)にxが棄却域に入らない(x<0.8)確率を考えます。
対立仮説が正しいとき、x-1が標準正規分布にしたがいますので、x<0.8 ⇒ x-1<-0.2となる確率を標準正規分布の付表より確認します。
「x-1=-0.2の下側確率」=「x-1=0.2の上側確率」を付表から探して、具体的にはβ=0.4207(≒0.421)と確認できます。
[29番] 点P(β, 1-α)が、x0の値に応じてどう変化するかを考えます。
- (前問[28]より)x0=0.8のとき、点P(β, 1-α)=P(0.421, 1-0.212)=P(0.421, 0.788)です。
- x0=0のとき、帰無仮説が正しいとき(平均θ=0のとき)にxが棄却域に入る(x≧0)確率α=0.5で、対立仮説が正しいとき(平均θ=1のとき)にxが棄却域に入らない(x<0 ⇒ x-1<-1)確率β=0.1587となります。つまり点P(β, 1-α)=P(0.1587, 0.5)です。
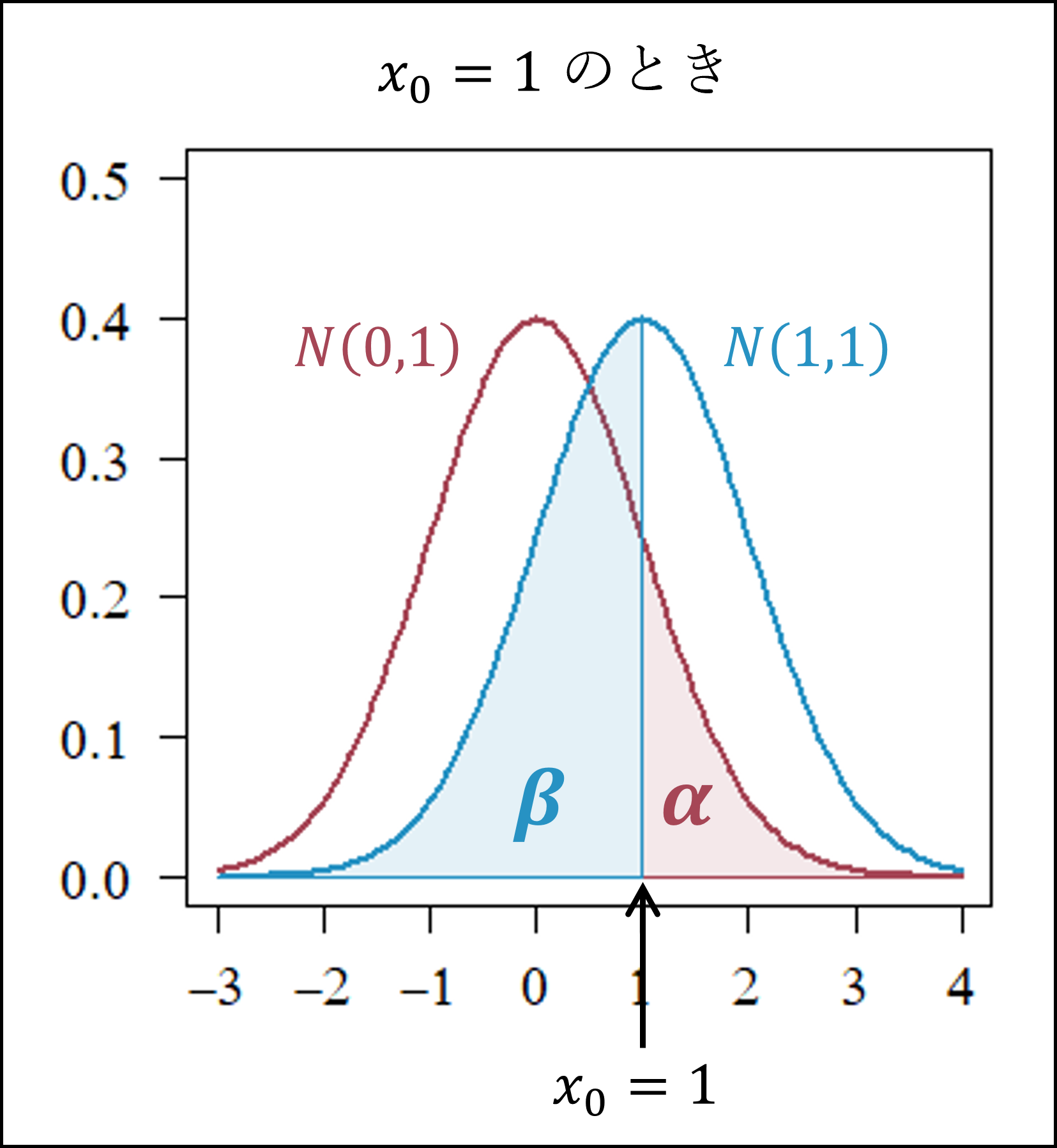
- x0=1のとき、帰無仮説が正しいとき(平均θ=0のとき)にxが棄却域に入る(x≧1)確率α=0.1587で、対立仮説が正しいとき(平均θ=1のとき)にxが棄却域に入らない(x<1 ⇒ x-1<0)確率β=0.5となります。つまり点P(β, 1-α)=P(0.5, 0.8413)です。
以上3つの点(0.1587, 0.5), (0.421, 0.788), (0.5, 0.8413)を平面上にプロットすると以下のようになります。
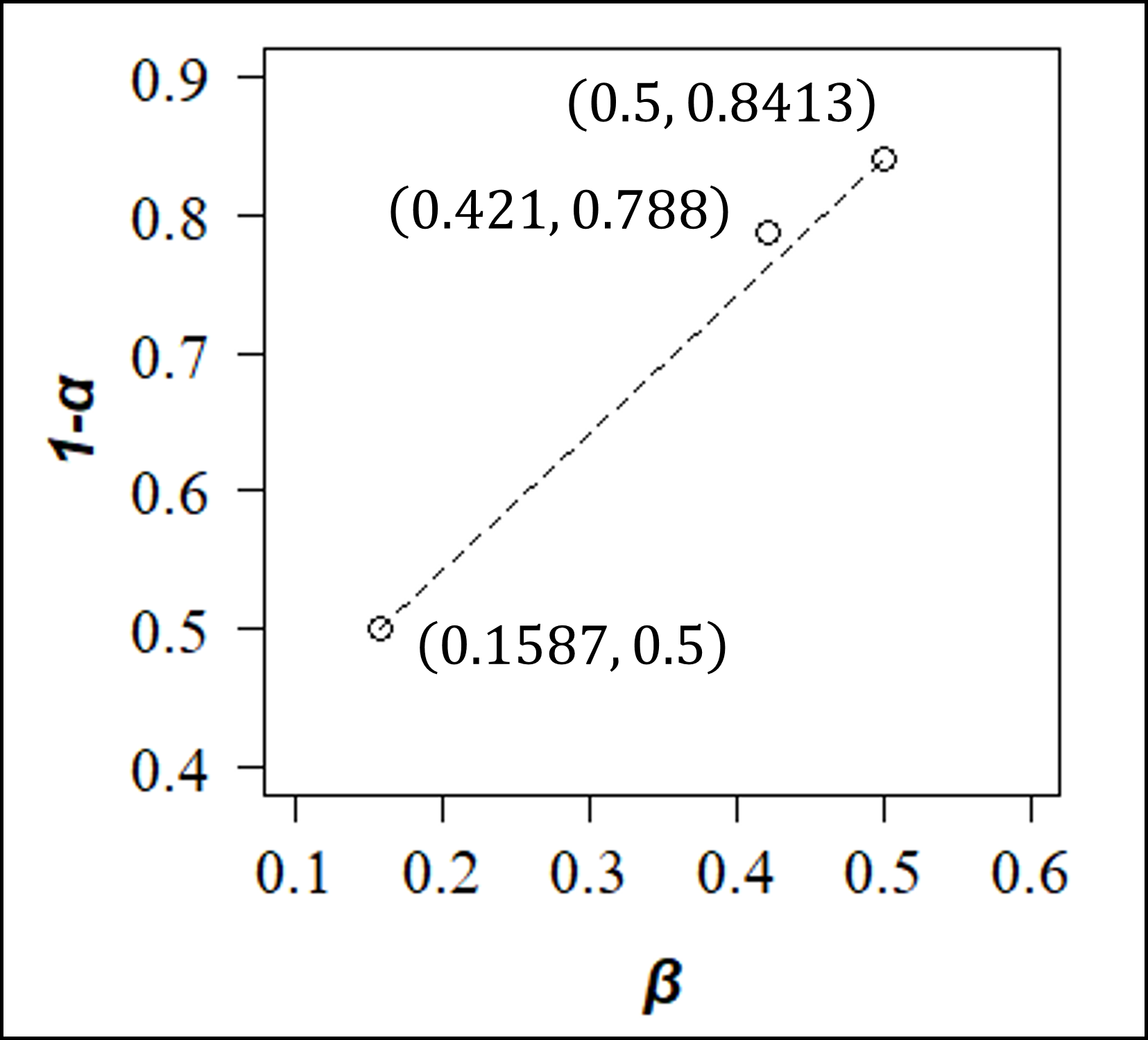
右肩上りとなりますが、直線とはならず、端点を結ぶ直線※よりも上側に少し膨らむようにカーブするような線となります。よって、選択肢①が正答になります。
[30番] 前問[29]で確認したx0=0、x0=0.8、x0=1のときについて、α+βの値を整理すると
- x0=0のとき、α+β=0.5+0.1587=0.6587
- x0=0.8のとき、α+β=0.212+0.421=0.633
- x0=1のとき、α+β=0.1587+0.5=0.6587
となります。これを用いて縦軸をα+β、横軸をxとするグラフを描くと以下のようになります。
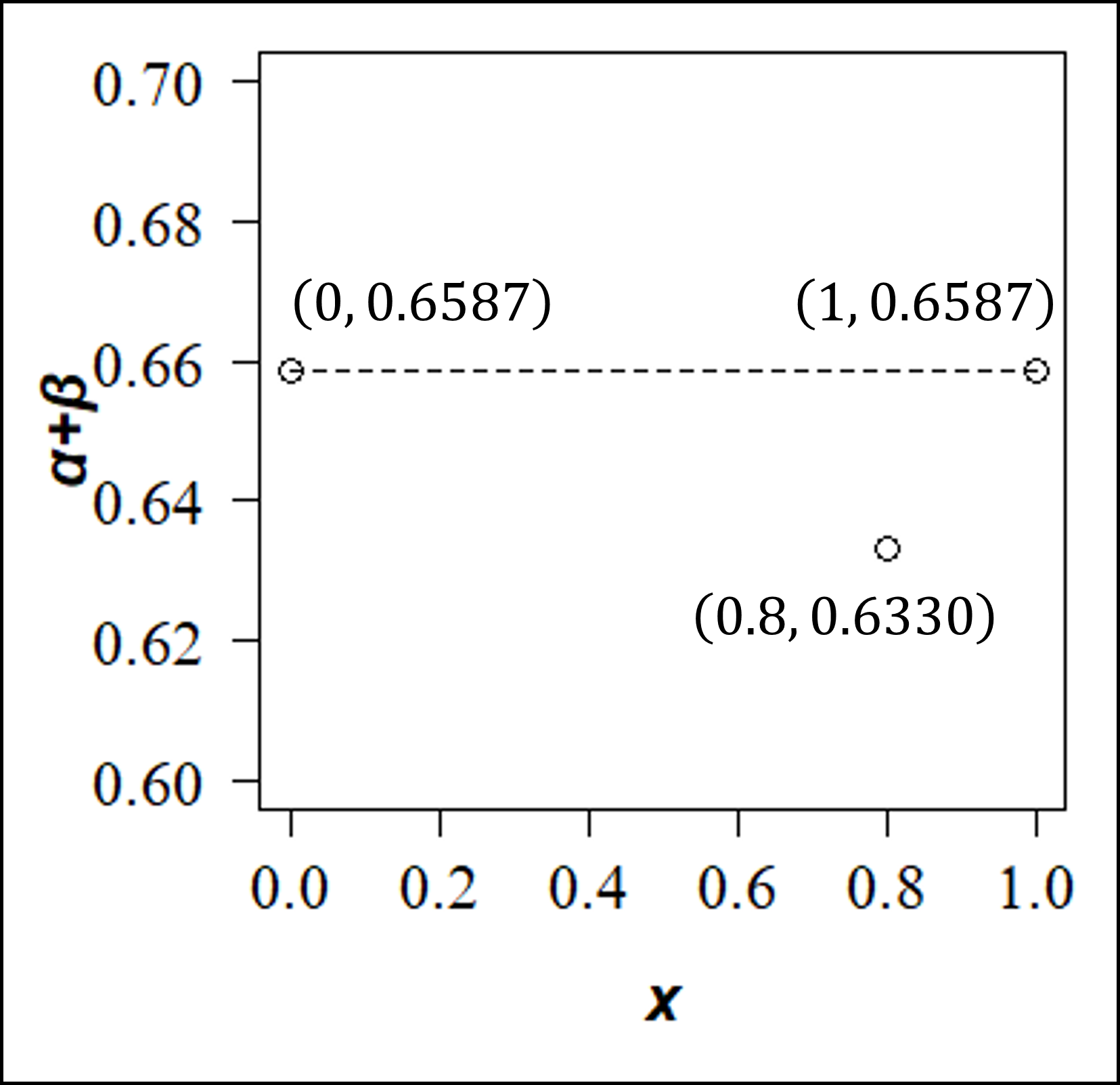
グラフから、縦軸のα+βが最小となるときは少なくともx=0やx=1のときではなく、xが0<x<1の間の値となるときであると確認できます。
したがって選択肢②が正答になります。
補足
- 第1種の過誤、第2種の過誤に関して深掘りする問題で難問です。
- [29番]で確認したプロットの端点を結ぶ直線は、傾きが (0.8413-0.1587)/(0.5-0.1587)=2で、切片が-0.1587となる直線で、つまりは「y=2x-0.1587」です。これにx=0.421を代入するとy=2×0.421-0.1587=0.6833となることから、点(0.421, 0.788)はこの直線よりも上側にあることが確認できます。
- [30番]のα+βは以下のように帰無仮説(赤色)と対立仮説(青色)の分布を描くと、x=0.5のときに最小となることに納得できるかと思います(分布の中央部分の方が確率密度が高くなりますので、帰無仮説・対立仮説ともに分布の中央部分が除外されるx=0.5のときにα+βが最小となります)。
ちなみに x=0 および x=1 のときはα+βは以下のようになります。
問17 [31,32,33番](2019年6月試験)
テーマ
- 重回帰モデル
- ダミー変数
- 決定係数
- 自由度調整済み決定係数
- 多重共線性
- 外挿
正答
[31番]選択肢② [32番]選択肢① [33番]選択肢⑤
解答例
[31番] 《記述Ⅰ》最終学歴は4つのカテゴリが存在するので、ダミー変数は4-1=3つ用意します。
4つのカテゴリすべてについてダミー変数を用意してしまうと、4つのうちの3つのダミー変数によって残りの4つ目のダミー変数を完全に説明できてしまい、多重共線性の問題が生じます。よって高校卒というダミー変数を加える必要はありません。
なお、高校卒と被説明変数(初任給)の関係は、他のすべてのダミー変数に0を代入したy=β1という式によって確認できます。
《記述Ⅱ》推定された偏回帰係数の値から、初任給は、
- 高校卒(H)であることに比べて大学卒(U)であることで4.450万円高い傾向
- 高校卒(H)であることに比べて大学院修士課程修了(G)であることで7.180万円高い傾向
が読み取れます。
したがって、初任給は、大学卒(U)であることに比べて大学院修士課程修了(G)であることで 7.180-4.450=2.73万円高い傾向があると考えられます。
《記述Ⅲ》偏回帰係数に関する検定統計量tは自由度がn-p-1(nはサンプルサイズ、pは説明変数の数)のt分布にしたがいます。よって、自由度はn-p-1=16-3-1=12になります。
[32番] 《記述Ⅰ》推定された回帰係数の値から、教育年数(x)が1年増えると被説明変数(初任給)が1.187万円高くなる傾向が読み取れます。
《記述Ⅱ》自由度調整済み決定係数は、説明変数の数に応じて自由度を用いて決定係数を調整したものです。決定係数および自由度調整済み決定係数の具体的には以下の式になります。

よって、単回帰モデルにおいても、説明変数p=1の分だけ全体平方和と残差平方和の自由度が異なりますので、決定係数と自由度調整済み決定係数は等しくなりません。
《記述Ⅲ》P-値は「実現した値よりも起こりづらい値となる確率」で、両側検定のときは分布の両側の確率を、片側検定のときは分布の片側の確率となります。
t分布は左右対称の分布であることから、片側検定のときのP-値は両側検定のときのP-値の半分になります。
[33番] 《記述Ⅰ》異なる説明変数を用いたモデルを比較する際は、説明変数の数を考慮した自由度調整済み決定係数を用いる必要があります。よって「誤り」です。
《記述Ⅱ》学歴ダミー変数を使った重回帰モデルでは、
- 高専/短大卒から大学卒に変わったときの初任給の変化 ⇒ 4.450-2.255=2.195万円
- 大学卒から大学院修士課程修了に変わったときの初任給の変化 ⇒ 7.180-4.450=2.73万円
というように、初任給の変化は個別に異なります。
一方で、学歴の情報を教育年数という1つの説明変数に集約した単回帰モデルでは、
- 高専/短大卒から大学卒に変わったときの初任給の変化
⇒教育年数が2年増えたときの初任給の変化 ⇒ 2年×1.187=2.374万円 - 大学卒から大学院修士課程修了に変わったときの初任給の変化
⇒教育年数が2年増えたときの初任給の変化 ⇒ 2年×1.187=2.374万円
というように、初任給の変化は等しくなります。
したがって「正しい」内容です。
《記述Ⅲ》「正しい」内容です。ただし、記述にあるように「外挿(観測された説明変数の値の区間を超えた値をモデルに代入して予測を行うこと)」に注意する必要があります。
補足
- ダミー変数の偏回帰係数は、そのダミー変数が、ダミー変数を用意しなかったカテゴリ(本問では「高校卒」)に比べてどれくらい被説明変数(初任給)に影響を及ぼすか、を表します。
問18 [34,35番](2019年6月試験)
テーマ
- 重回帰モデル
- 偏回帰係数の検定
正答
[34番]選択肢⑤ [35番]選択肢③
解答例
[34番] 出力結果から各偏回帰係数および定数項のP-値を確認すると、いずれも5%以下となっていますので、すべて(定数項および2つの偏回帰係数)の係数が有意となります。
※「2e-16」というのは「2×10^(-16)」、すなわち、「2×”10の-16乗”」を意味します。
[35番] 《選択肢①》一般に自由度調整済み決定係数は決定係数よりも小さくなります。正規性の仮定(正規分布にしたがうという前提)を疑うという話ではありませんので「誤り」です。
《選択肢②》t統計量(t value)は説明力をあらわすものではなく、偏回帰係数が0であるという帰無仮説を検定する際の検定統計量で、変数の説明力を表すものでありません。
《選択肢③》「正しい」内容です。冒頭の「他の変数が同じ値である場合~」という但し書きがとても重要です。
《選択肢④》F統計量(F-statistic)は回帰モデル全体の有意性を検定するための検定統計量で、各係数が0であるという帰無仮説の検定に用いられるものではありませんので「誤り」です。
《選択肢⑤》重回帰分析で変数選択を行うときは、自由度調整済み決定係数(Adjusted R-squared)を用います。決定係数(Multiple R-squared)では説明変数の数を考慮した比較を行えません。
補足
- なお、出力結果の「Residual standard error :」は「残差の標準誤差」で、「44 degrees of freedom」は残差平方和の自由度が44(=n-p-1)であることを意味しています。

