
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問01 [01,02,03番](2018年11月試験)
テーマ
- 相対度数分布表
- 箱ひげ図
正答
[1番]選択肢⑤ [2番]選択肢① [3番]選択肢③
解答例
[1番] 各階級の相対度数の合計は100(%)となりますので(ア)は100-85.1-2.1=12.8(%)となります。また、(イ)は100-76.6-17.0-2.1=4.3(%)となります。
なお、一般に相対度数分布表は観測されるすべての階級を表にしますので「140校以上」となる都道府県が存在する可能性を考慮する必要はありません(まぎらわしいので「120校以上140校未満」という階級は「120校以上」としてくれるとありがたいのですが…)。
[2番] 「40校以上60校未満」にプロット(観測値)のある箱ひげ図はCだけですので、Cが「2017年」の箱ひげ図です。また、「20校以上40校未満」にプロット(観測値)のない箱ひげ図はAだけですので、Aが「1952年」の箱ひげ図で、残ったBが「1985年」の箱ひげ図となります。
[3番] 《記述Ⅰ》四分位範囲は1952年より1985年の方が大きく、1985年より2017年の方が大きいので、誤りです。
《記述Ⅱ》箱ひげ図から1952年の最大値は70~75校程度で、1985年の最大値は100~105校程度と読み取れますので、誤りです。
《記述Ⅲ》中央値は箱ひげ図の箱の中の黒い線で表示されます。記述の通り1952年よりも1985年の方が、1985年よりも2017年の方が中央値は大きくなっていますので、正しいです。
補足
- 大学数が圧倒的に多いのは「東京都」だと推察できますが、これほどまでに他の都道府県よりも東京都の大学数が多いことに驚かされました(問題とは関係ありません)。
問02 [04番](2018年11月試験)
テーマ
- 相関係数
- 時系列データ
正答
選択肢①
解答例
《記述Ⅰ》正しい内容です。賃金との相関係数は「男性・正社員」で0.58、「男性・正社員以外」で0.80で、正社員の方が相関係数の絶対値が小さくなっています。
ただし、「男性・正社員」では50歳を境に賃金が増加傾向から減少傾向へと変化しており、傾きが一定の直線では表現できない関係が存在しています。そのため、傾きが一定の直線関係を前提とする相関係数だけで関係性の強弱を判断することはできません。
《記述Ⅱ》「女性・正社員」は55歳以降で賃金が減少傾向となっており、55歳以降のデータが相関係数をマイナス側へ押し下げています。したがって55歳以降のデータを除く20~54歳のデータのみで相関係数を計算すると元の相関係数0.56よりも大きい値となります。よって誤りです。
《記述Ⅲ》誤りです。「年齢が1歳上がると賃金が0.46万円下がる」という解釈は単回帰分析の回帰係数についての解釈で、単に直線関係を示す指標である相関係数の解釈としては不適切です。
補足
- 相関係数は常に傾きが一定の直線関係を前提としますので、本問の「男性・正社員」のようにある値を境に傾向が変化するような関係性をうまく捉えられませんので注意しましょう(年齢と体重の関係、年齢と身長の関係、などもある年齢を境に増加傾向から減少傾向に変化するため同じような問題を作れそうです)。
問03 [05,06番](2018年11月試験)
テーマ
- 時系列データ
- 指数化
- 3項移動平均
正答
[5番]選択肢① [6番]選択肢④
解答例
[5番] 2017年1月の価格指数の前月比変化率が4.98%ですので、2017年1月の価格指数を「÷1.0498」すると前月(2016年12月)の価格指数となります。
具体的には111.7÷1.0498=106.40…≒106.4となります。
[6番] 3項移動平均は連続する3つの項(時点)の平均をとったものです。連続する3つの項の平均をとっている選択肢は④のみですので、選択肢④が正答です。
補足
- 「3項移動平均」とあれば一般には基準時点および基準時点の前後の時点(基準時点をt時点とすると、「t-1時点」「t時点」「t+1時点」の3時点)を抽出して平均をとりますが、「t-2時点」「t-1時点」「t時点」の3時点とすることや、「t時点」「t+1時点」「t+2時点」の3時点とすることもありますので、問題文を注意深く読むようにしましょう。
問04 [07番](2018年11月試験)
テーマ
- 価格指数
- ラスパイレス価格指数
正答
選択肢②
解答例
ラスパイレス価格指数は以下の式により計算されます(参考までにパーシェ式の計算式も掲載しています)。
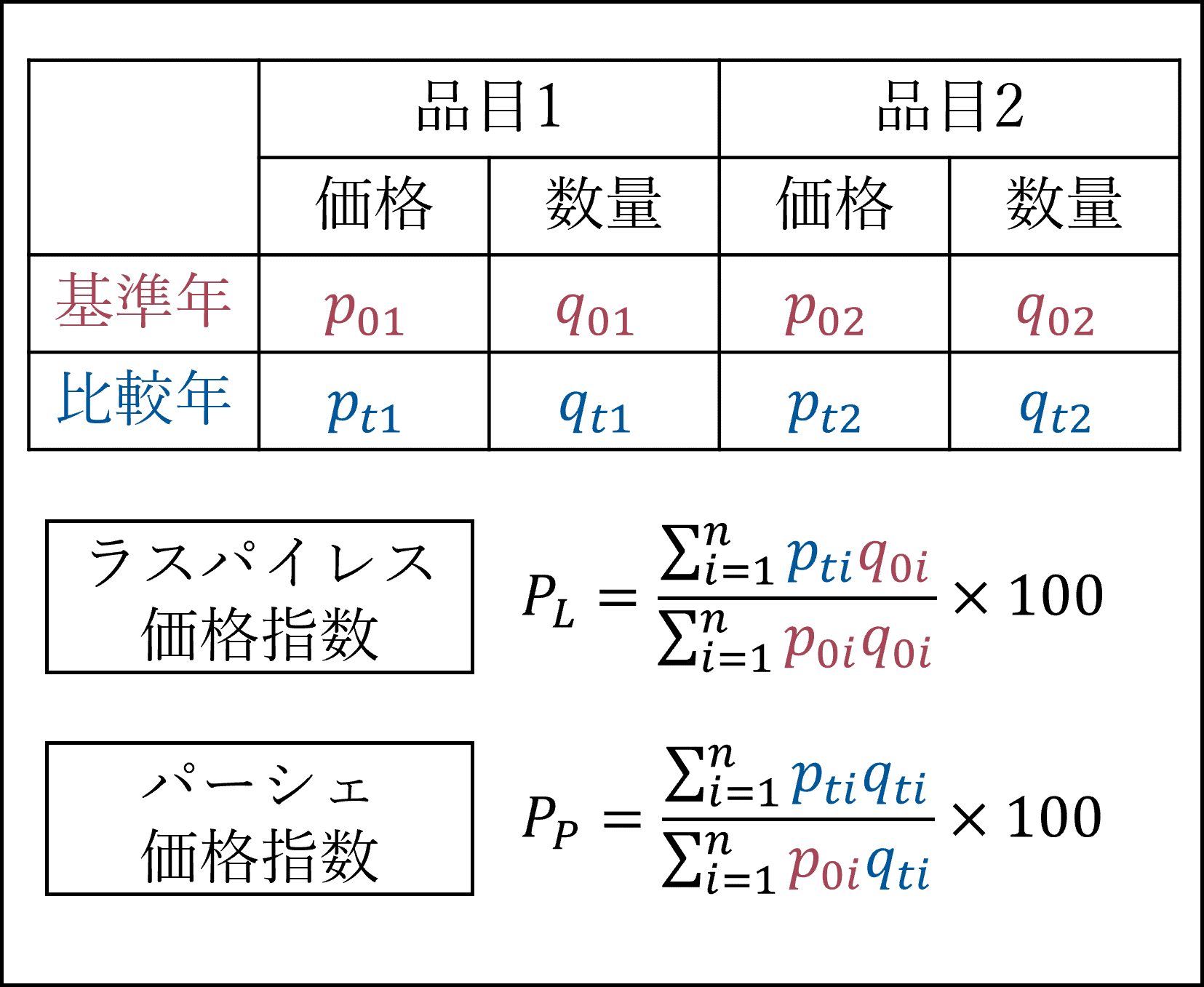
今回のケースでは以下のようになります(参考までにパーシェ式も計算してあります)。
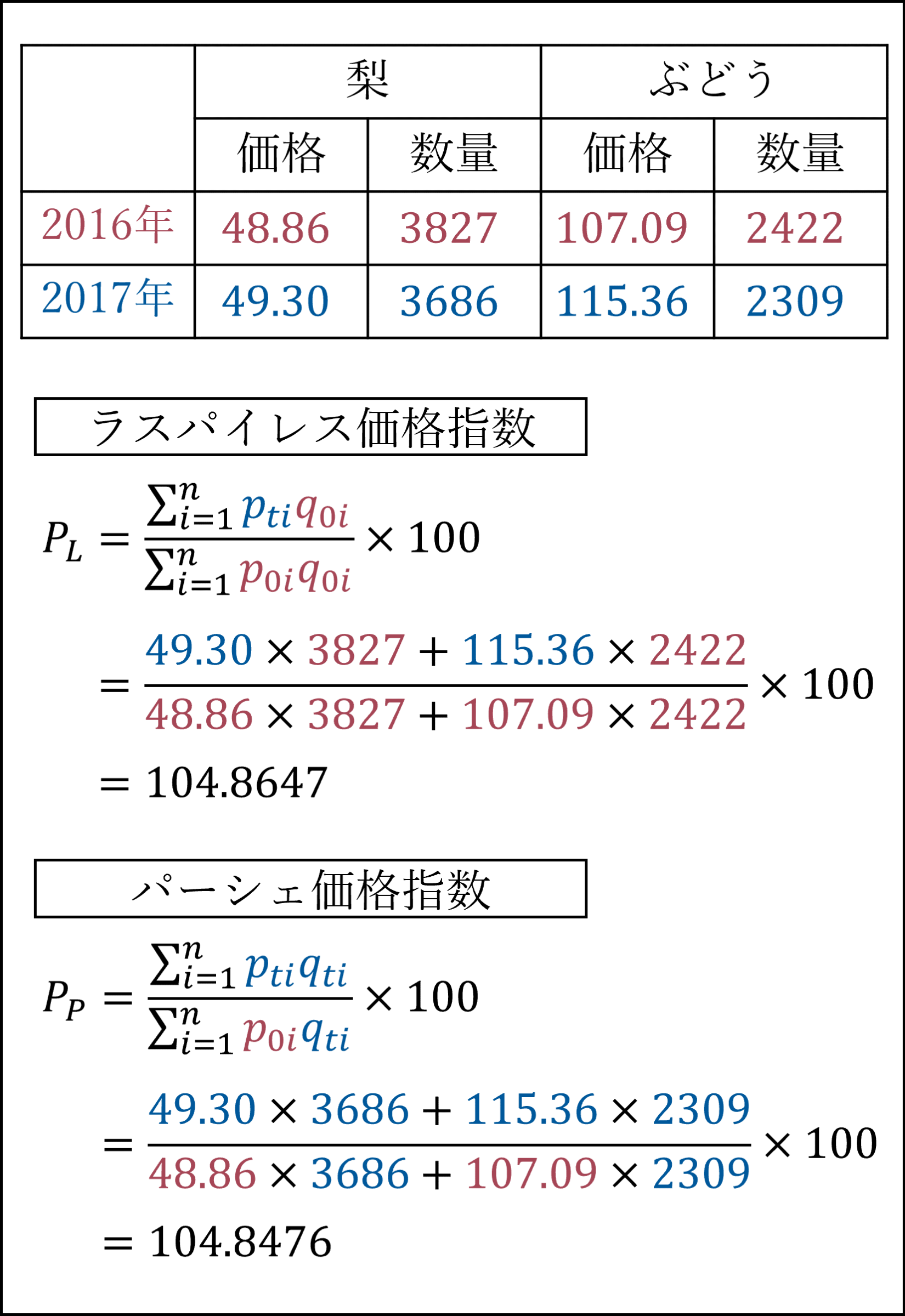
補足
- ラスパイレス式価格指数の数量情報は基準年の情報をベースとしていますので、比較年の数量を調査する必要がないという利点があります。
問05 [08番](2018年11月試験)
テーマ
- 単純無作為抽出
- 層化抽出
正答
選択肢③
解答例
《記述Ⅰ》正しい内容です。公式テキスト『統計学基礎』に記載された単純無作為抽出の解説と対応する内容ですので、こちらの記述内容を単純無作為抽出の定義として理解しておくとよいかと思います。
《記述Ⅱ》誤りです。層化抽出によって分散を小さくできるのは、一般に「層内の分散」です。「母集団平均の推定量の分散」には「層内の分散」だけでなく「層間の分散」も影響を及ぼしますので、これが一概に小さくなるとは言い切れません。
《記述Ⅲ》正しい内容です。例えば血液型別の調査を行おうとする際に、(仮に)AB型の割合が極端に小さい国であれば、単純無作為抽出ではAB型の人が抽出されない可能性があります。
補足
- 記述Ⅰが少しややこしいですが、単純無作為抽出は「完全にランダム」とイメージしておくとよいかと思います(「完全にランダム」なはずなのに「特定の組が抽出される確率に偏りがある」というのはおかしいと気づけそうです。)。
問06 [09番](2018年11月試験)
テーマ
- 二段抽出
正答
選択肢②
解答例
1段階目で市区町村を抽出し、2段階目で世帯を抽出する「二段抽出」の説明になります。
補足
- 二段抽出と層化抽出で迷う方もいるかもしれませんが、二段抽出はtwo-stage samplingで、層化抽出はstratified samplingと英語で意識する違いがわかりやすいかと思います。
問07 [10,11番](2018年11月試験)
テーマ
- 条件付き確率
- ベイズの定理
正答
[10番]選択肢② [11番]選択肢②
解答例
[10番] カモノハシの絵のクッキーである確率を、工場Aと工場Bの各々で計算して合計します。
・工場A:0.7×0.02=0.014
・工場B:0.3×0.08=0.024
・合計:0.014+0.024=0.038
よって正答は0.038となります。
[11番] ベイズの定理で「カモノハシの絵であるという結果を得られたときの原因が工場Aである確率」を求めましょう。ベイズの定理より求める確率について
・分子:工場Aの確率×工場Aでカモノハシの確率=0.7×0.02=0.014
・分母:(工場Aの確率×工場Aでカモノハシの確率)+(工場Bの確率×工場Bでカモノハシの確率)=(0.7×0.02)+(0.3×0.08)=0.038
よって求める確率は0.014 / 0.038≒0.368となります。
ベイズの定理に苦手意識がある場合は以下のように表に整理すると考えやすいかと思います。
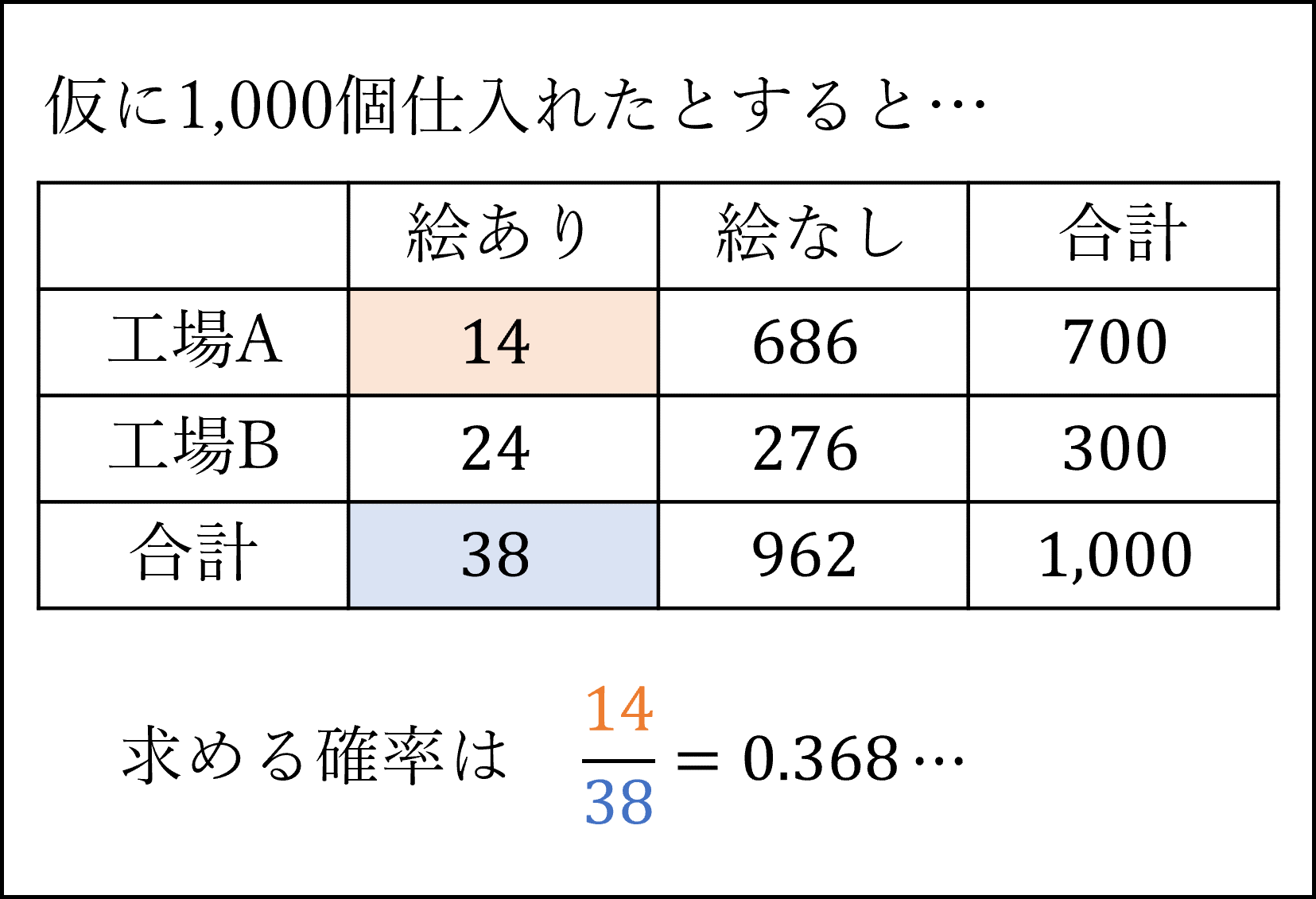
補足
- 慣れてくるとベイズの定理の方が速いかもしれませんが、表に整理したほうが考えやすいかと思います。表にした方が視覚的な安心感がありそうです。
問08 [12,13番](2018年11月試験)
テーマ
- 標準正規分布
- 確率変数の線形変換
正答
[12番]選択肢④ [13番]選択肢①
解答例
[12番]問題文から確率変数Uが標準正規分布にしたがうことがわかっていることを踏まえ、P(Y≧0)=0.95という式の左辺の条件式について以下のように整理します。
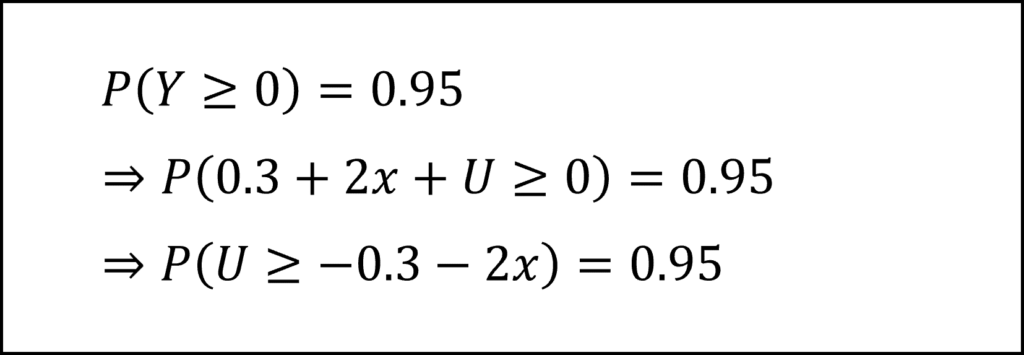
したがって、確率変数Uが「-0.3-2x以上となる確率が0.95(=95%)」と整理できます。
ここで、確率変数Uは標準正規分布にしたがいますので、「-0.3-2x」は標準正規分布の上側95%点(下側5%点)となります。標準正規分布の上側95%点(下側5%点)は-1.645ですので、以下のようにxを導くことができます。
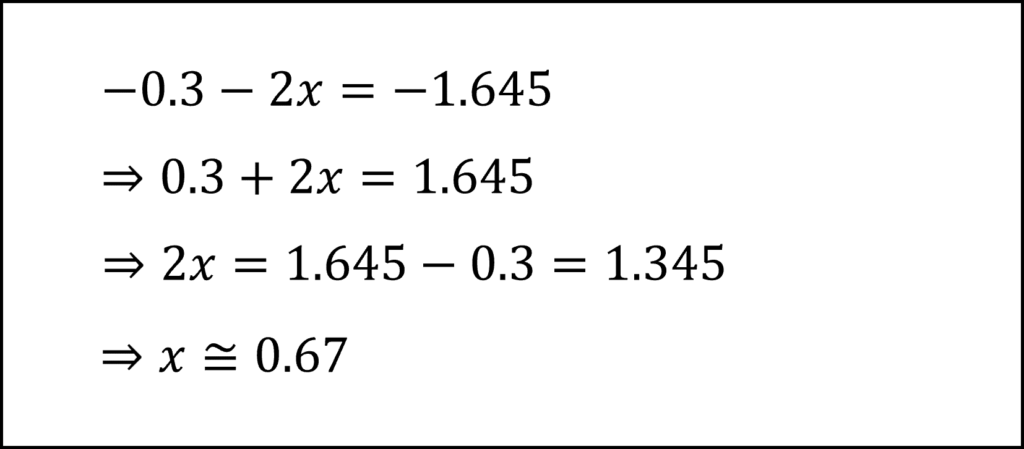
[13番]問題文に与えられているYとUの関係式から、Yの上側5%点はUの上側5%点に「0.3+2x」を加えたものになります。
また、Uは標準正規分布にしたがいますので、Uの上側5%点は1.645です。したがって、Yの上側5%点は、0.3+2x+1.645=1.945+2xとなります。
例えば、x=0のときのYの上側5%点は、上記式にx=0を代入して1.945となり、このことだけからも選択肢①が正答と読み取れます。
補足
- [12番]は上側5%点ではなく、上側95%点であることに注意しましょう。
- [13番]はYの上側5%点を、0.3+2x+[Uの上側5%点]=0.3+2x+1.645=1.945+2xと整理したところで、グラフはxの「線形」関数になることが明らかですので、この段階で選択肢①を選ぶこともできます。
問09 [14,15番](2018年11月試験)
テーマ
- 二項分布の確率関数
正答
[14番]選択肢② [15番]選択肢②
解答例
[14番]1回の試行で2以下の目が出る確率は1/3ですので、Xは試行回数n=7回、成功確率p=1/3の二項分布Bin(7,1/3)にしたがいます。したがって、二項分布の確率関数より、X=xとなる確率P(X=x)は以下の関数で導かれます。
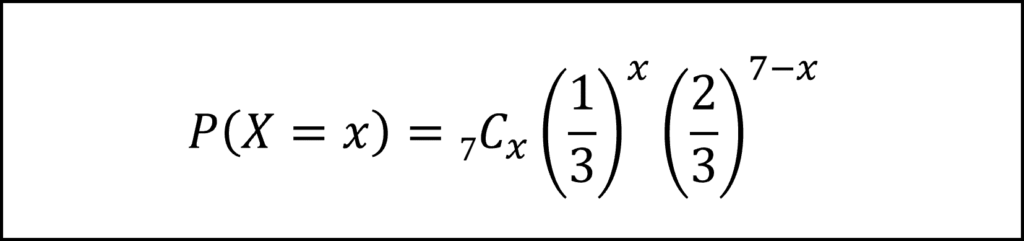
ここで、X=0のときを考えると、問題文に与えられた式にx=0を代入することで以下の式①が得られます。
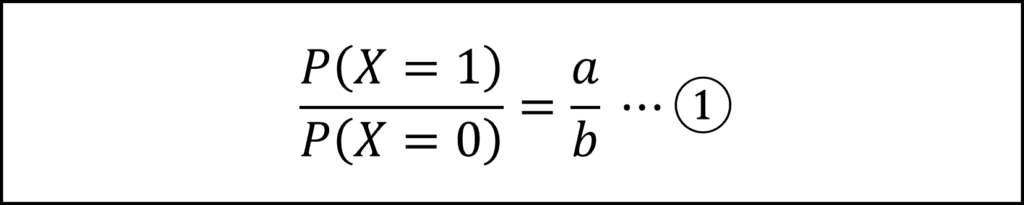
この式の左辺を、先ほど求めた二項分布の確率関数を用いて整理すると式②を得られます。
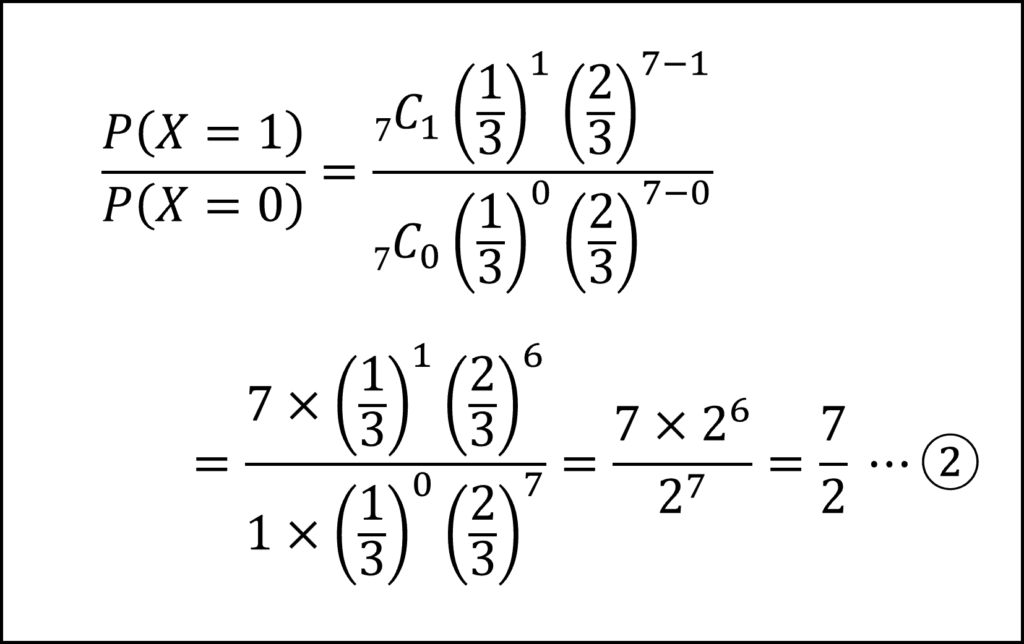
式①と式②を対応させると、a=7、b=2と導くことができます。
[15番]前問の答えから以下の式③を得られます。
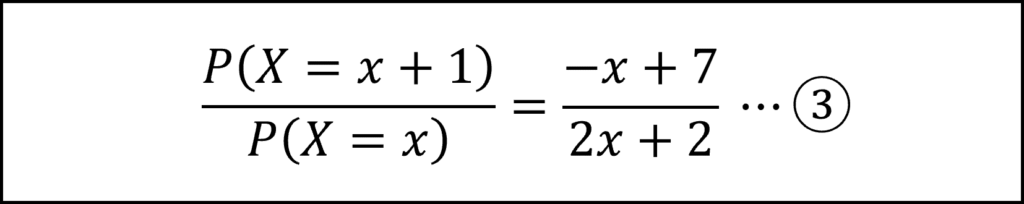
ここで、P(X=x)が最大、つまり、X=xのときの確率が最大となるとき、P(X=x)はP(X=x+1)より大きくなるので、式③は1より小さくなるはずです。したがって、以下のように不等式を設定、整理できます。
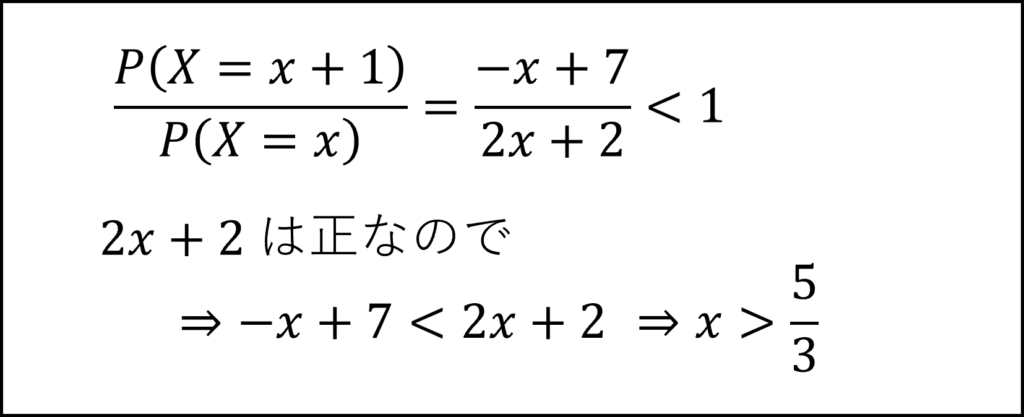
xは0から6の整数ですので、x>5/3を満たす最小の整数である選択肢②が正答となります。
補足
- やや難問です。問題文の意図がわかれば二項分布の確率関数から簡単に導けるのですが、問題文の意図を読み取ることがやや難しいです。
- 二項分布の確率関数は組合せの数が登場して式が複雑になりますが、具体的な値を代入してみると考えやすいです(ここではX=0のときを考えることでスムーズに解答できました)。
- なお、[15番]は二項分布の期待値がnpであることから、ここでは期待値がnp=7×(1/3)≒2.33ということから、X=2.33の近くで確率が最大となるとアタリをつけてもよいでしょう(分布の形状にもよりますのでこの方法の採用は慎重に)。
問10 [16番](2018年11月試験)
テーマ
- 標本平均の期待値と分散
正答
選択肢③
解答例
互いに独立な確率変数の平均(標本平均)の期待値は、各々の確率変数の期待値μを用いて、以下のように整理されます。
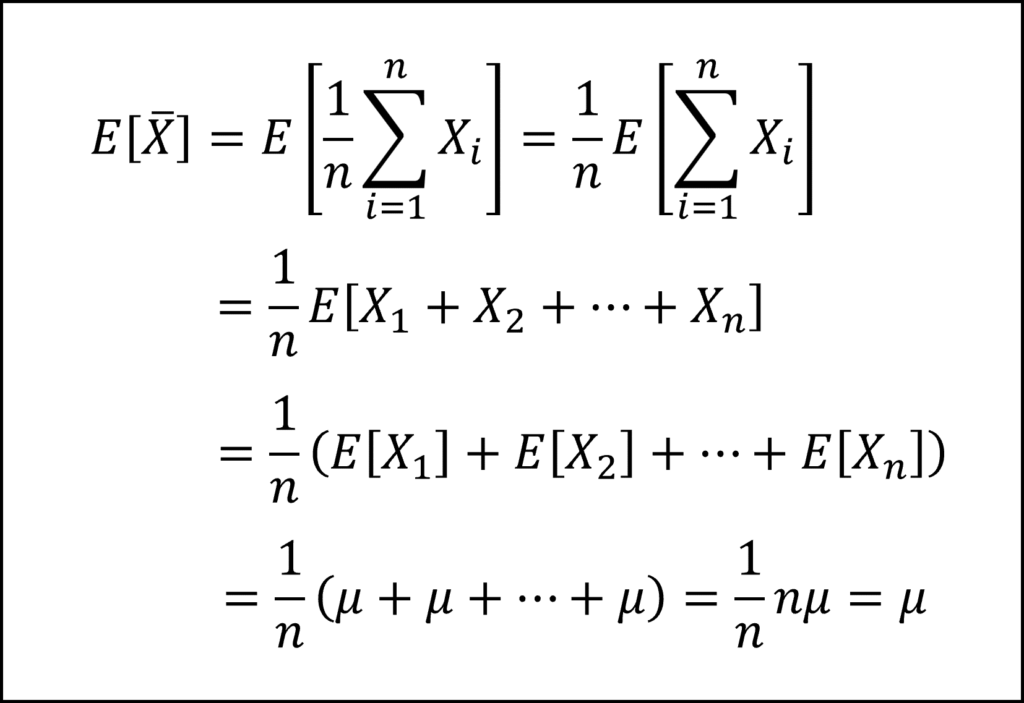
また、互いに独立な確率変数の平均(標本平均)の分散は、各々の確率変数の分散σ^2を用いて、以下のように整理されます。
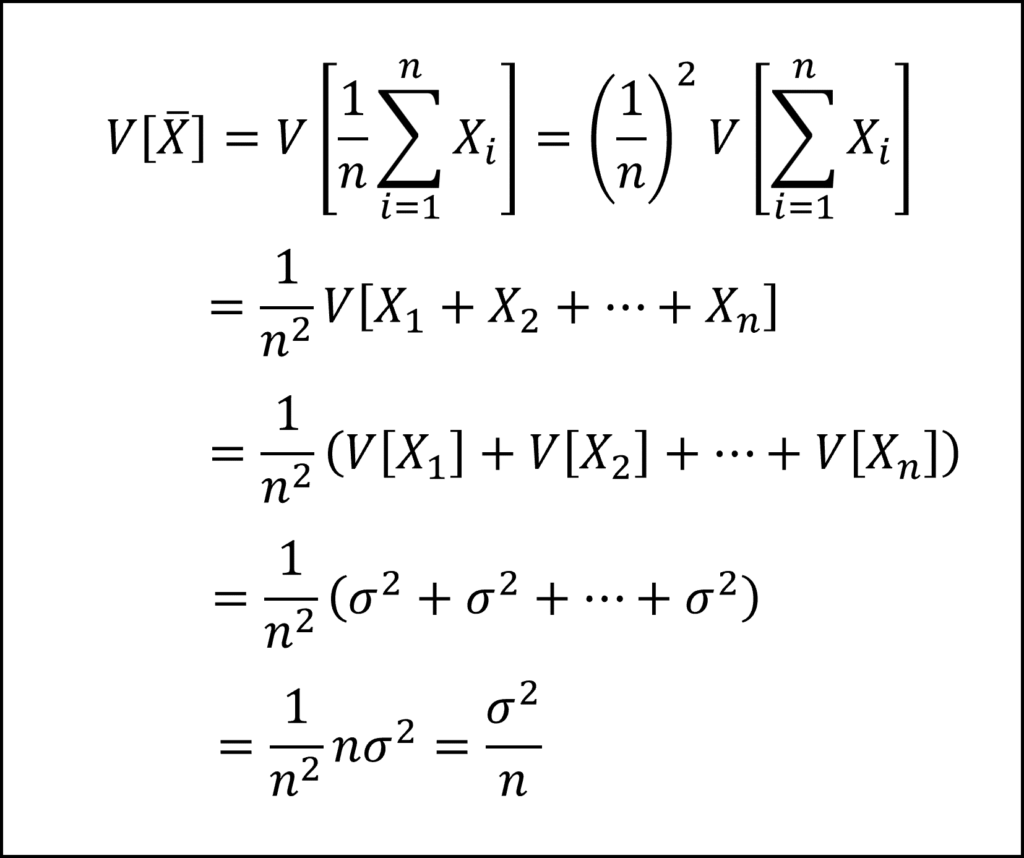
互いに独立であることから、和の分散V[ΣXi]は、分散V[Xi]の和と展開できることに注意しましょう。
補足
- とてもシンプルな問題で、逆に、何か落とし穴や見過ごしがあるのでは…?と思えそうな問題です(特にそういうことはないのですが…)。
- 仮に各々の確率変数が「互いに独立ではない」のであれば、分散の導出において各々の確率変数の組における共分散が必要になります。
問11 [17,18,19番](2018年11月試験)
テーマ
- 歪度
- 尖度
正答
[17番]選択肢① [18番]選択肢⑤ [19番]選択肢⑤
解答例
[17番]正規分布にしたがう確率変数の歪度は0、尖度も0(尖度をμ/σ^4と定義する場合は3)となります。
[18番]一様分布は左右対称な分布ですので正規分布と同様に歪度は0になります。
一方で、一様分布は正規分布よりも「尖りのない」分布(別の言い方をすると「裾が厚い」分布)ですので、尖度は正規分布よりも小さくなります。正規分布の尖度は0なので、一様分布の尖度は負の値となります。
5つの選択肢のうち歪度が0で尖度が負の値となる選択肢⑤が正答になります。
[19番]《記述Ⅰ:誤り》右に裾が長い分布の歪度は正の値になり、左に裾が長い分布の歪度は負の値になります。「うっせいわい(右・正・歪)」と覚えましょう、という話でした。
《記述Ⅱ:誤り》正規分布よりも中心が平坦で裾が厚い分布の尖度は負の値となります。上述した通り、正規分布よりも「尖りのない」分布、あるいは、「裾が厚い」分布であれば、尖度は正規分布の尖度0より小さく負の値となります。
《記述Ⅲ:誤り》t分布は左右対称な分布なので歪度は0になります。
また、t分布は正規分布よりも「尖りのない」分布、あるいは、「裾が厚い」分布ですので、尖度は負の値となります。このとき、t分布は自由度が大きくなると正規分布に近づきますので、自由度が大きくなるほどt分布の尖度は正規分布の尖度0に近づきます。したがって、自由度が大きいほど尖度の絶対値は小さくなります。
補足
- 歪度は分布の歪みに関する指標で、尖度は分布の尖りに関する指標になります。
- 尖度は「尖り」や「裾の厚み」に着目することで混乱を軽減できます。

