
準1級文系解説について(各回共通)
ご訪問いただきありがとうございます。こちらは統計検定🄬準1級合格を目指す方が、公式テキスト『統計学実践ワークブック』やそのほか統計検定🄬準1級対策コンテンツをスラスラと学び進めるために必要な解説を行うブログです。
本ブログは、公開されている「統計検定🄬準1級出題範囲」の各項目について執筆しています。「統計検定🄬準1級出題範囲」は『統計学実践ワークブック』の内容にも対応していますので、本ブログの解説が『統計学実践ワークブック』の読解に役立つ部分も多くあるかと思います。その意味で、本ブログをご覧いただく方には、公式テキスト『統計学実践ワークブック』を購入されることを推奨いたします。
なお、統計検定🄬は一般財団法人統計質保証協会の登録商標です。また、本ブログは一般財団法人統計質保証協会から公認されたコンテンツではありません。
00. はじめに
「確率という言葉を聞くだけで、なんだか頭が痛くなる…」
「公式はなんとなく覚えたけど、どの問題でどう使えばいいのかサッパリ…」
統計学の学習で、多くの人が最初にぶつかる壁、それが「確率」です。特に、数学から少し距離を置いてきた文系の方にとっては、手強い相手に感じるかもしれません。でも、安心してください。確率は、決して一部の理系(?)の人だけのためのものではありません。実社会の様々な問題を読み解き、より良い意思決定をするための強力な「武器」にもなるものです。
この記事では、準1級の合格を目指すあなたが、確率の基本をマスターし、応用問題にも自信を持って挑めるようになることを目指します。特に、今回のテーマを攻略するために不可欠な以下の知識を、ひとつひとつ丁寧に見ていきましょう。
- 条件付き確率:「もし〜が起こったら?」という、未来を予測する思考法
- ベイズの定理:得られた情報から「原因」をさかのぼる、まるで探偵のようなテクニック
- 確率変数:事象の結果を「確率」というメガネを通して表現するもの
- 期待値と分散:データ全体の「平均的な姿」と「ばらつき具合」を捉える二大巨頭
Udemyで統計学を教えてきた経験から、独学で「どこにつまずきやすいか」を少しはおさえているつもりです。この記事を読み終える頃には、今までぼんやりとしていた確率の世界が、クリアに見えてくるかもしれません。さあ、一緒に確率の第一歩を踏み出しましょう!
01. 事象と確率
まずは基本から。事象とは、試行(サイコロを振る、コインを投げるなど)によって起こりうる「できごと」のことです。「サイコロを振って1の目が出る」とか、「明日の天気は晴れだ」とか、そういったものですね。

そして確率とは、ある事象がどれくらいの「起こりやすさ」で発生するかを 0 から 1 の間の数値で表したものです。基本は以下の計算式となります。
\[
P(A)=\frac{起こりうるすべての場合の数}{事象Aが起こる場合の数}
\]
例えば、「6面のサイコロを1回振って偶数の目が出る確率」は、全体の場合の数が6通り(1, 2, 3, 4, 5, 6)、偶数の目が出る場合の数が3通り(2, 4, 6)なので、 \( 3/6=1/2\) となります。簡単です…かね?
02. 包除原理(ほうじょげんり)
では、「サイコロを振って、2以下の目 または 5以上の目が出る確率」はどうでしょう?「2以下の目が出る事象」を \(A\) 、「5以上の目が出る事象」を \(B\) とします。すると、 \(P(A)=2/6\) 、 \(P(B)=2/6\) ですね。この場合、 \(A\) と \(B\) は同時には起こらないので、単純に足し算して \(P(AまたはB)=2/6+2/6=4/6\) となります。

しかし、「3の倍数 または 偶数が出る確率」となると話は少し変わります。「3の倍数が出る事象」を \(C\) (3, 6の2通り)、「偶数が出る事象」を \(D\) (2, 4, 6の3通り)としましょう。すると \(P(C)=2/6\) 、 \(P(D)=3/6\) です。
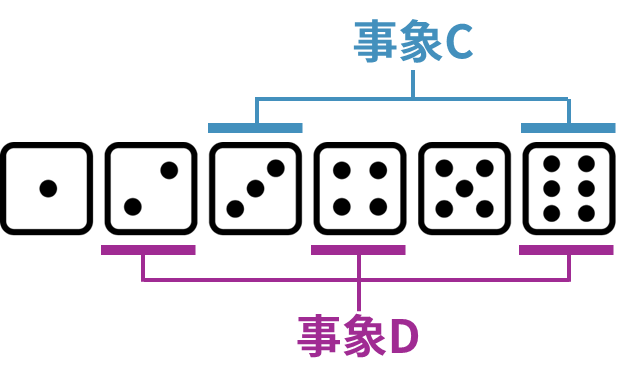
これを単純に足すと \(2/6+3/6=5/6\) となりそうですが、これは間違いです。なぜなら、「6」という目が両方でカウントされてしまっているからです。このように、ダブルカウントした部分を引く、というのが包除原理の考え方です。数式で書くと以下のようになります。
\[
P(C∪D)=P(C)+P(D)−P(C∩D)
\]
この \(C∪D\) は「 \(C\) または \(D\) が起こる」、 \(C∩D\) は「 \(C\) かつ \(D\) が起こる」という意味です。 \(P(C∩D)\) は「3の倍数であり、かつ偶数である」確率、つまり「6の目が出る」確率なので \(1/6\) です。よって、正しくは \(2/6+3/6-1/6=4/6\) となります。ベン図を思い浮かべると、2つの円が重なる部分を一度引いているイメージですね。
03. 条件付き確率
ここからが本番です。条件付き確率は、準1級で頻出の超重要テーマ。これは、「ある事象 \(B\) が起こった、という条件下で、事象 \(A\) が起こる確率」のことで、 \(P(A \mid B)\) と書きます。真ん中の「 \(\mid\) 」が、「という条件下で」という区切り線だと思ってください。
つまずきポイント:
多くの人が、 \(P(A∩B)\) (AかつBが起こる確率)と \(P(A \mid B)\) (Bが起こった後でAが起こる確率)を混同してしまいます。イメージとしては、 \(P(A∩B)\) の分母は「起こりうるすべての事象」ですが、 \(P(A \mid B)\) の分母は「事象 \(B\) が起こったという世界」に限定されます。見る範囲(全体)がギュッと狭まる感じです。公式は以下の通りです。
\[
P(A \mid B)=\frac{P(A∩B)}{P(B)}
\]
この数式は、「 \(B\) が起こる確率を分母(新しい全体)にして、その中で \(A\) も \(B\) も起こっている確率(分子)の割合を見ていますよ」と示してくれています。例えば、「トランプのジョーカーを除いた52枚から1枚引いたら、それがハートだった(事象 \(B\) )。そのカードが絵札(K, Q, J)である(事象 \(A\) )確率」を考えてみましょう。
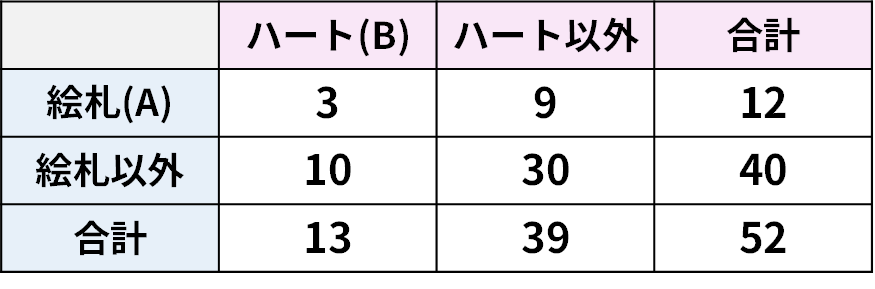
ハートは13枚ありますから、 \(P(B)=13/52\) です。
ハートの絵札は3枚なので、\(P(A∩B)=3/52\) です。
よって、 \(P(A \mid B)=\dfrac{3/52}{13/52}=3/13\) となります。
直感的にも、「ハート13枚の中に絵札は何枚ある?」と考えて \(3/13\) と計算できますよね。これが条件付き確率の本質です。
04. 統計的独立
もし、事象 \(B\) が起ころうが起こるまいが、事象 \(A\) の確率に全く影響を与えない場合、この2つの事象は統計的に独立である、と言います。つまり、 \(P(A \mid B)=P(A)\) が成り立つ状態です。この式を先ほどの条件付き確率の公式に代入すると、有名な独立の定義式が導かれます。
\[
P(A∩B)=P(A)P(B)
\]
事象 \(A\) と \(B\) が独立なら、「 \(A\) と \(B\) が両方起こる確率」は、それぞれの確率を掛け算するだけで求められる、という便利な性質です。
05. ベイズの定理
さあ、いよいよボスキャラの登場です。ベイズの定理は、条件付き確率を応用したもので、「ある結果(事象 \(B\) )が観測されたとき、その原因が \(A\) であった確率(事象 \(A\) )はどのくらいか」を計算できます。例題でよく出るのは、「ある検査で陽性反応が出た(結果)とき、本当にその病気にかかっている(原因)確率は?」といった問題です(多くの場合、陽性でも本当に病気である確率は意外と低い…)。ここでいくつか用語を押さえましょう。
- 原因事象:知りたいこと(例:病気にかかっているか否か)
- 結果事象:観測されたデータ(例:検査結果が陽性か陰性か)
- 事前確率:結果を知る「前」の確率。 \(P(A)\) のこと。(例:一般の人がその病気にかかっている確率)
- 事後確率:結果を知った「後」の確率。 \(P(A \mid B)\) のこと。(例:検査で陽性と出た後で、本当に病気である確率)
ベイズの定理は、事前確率を、得られたデータ(結果)を使って事後確率に更新していくプロセスと考えることができます。公式は以下のとおりです。1つ目の「=」は条件付き確率の計算式、2つ目の「=」では \(P(A∩B)=P(B \mid A)P(A)\) と展開していて、この結果がベイズの定理といわれる式になります。
\[
P(A \mid B)=\frac{P(A∩B)}{P(B)}=\frac{P(B \mid A)P(A)}{P(B)}
\]
この式を見て「うっ…」となった方、大丈夫です。分解してみましょう。
- \(P(A \mid B)\) :求めたい事後確率(結果 \(B\) のもとでの原因 \(A\) の確率)
- \(P(B \mid A)\) :原因 \(A\) のもとで結果 \(B\) が起こる確率(これは問題文で与えられることが多い。例:病気の人が陽性になる確率)
- \(P(A)\) :事前確率(原因 \(A\) がそもそも起こる確率)
- \(P(B)\) :結果 \(B\) が起こる確率(これは少し厄介)
つまずきポイント:
一番の難関は分母の \(P(B)\) の計算です。これは「全確率の定理」という考え方を使います。例えば、「検査で陽性になる( \(B\) )」という結果は、次の2つのパターンに分けられます。
- 本当に病気で( \(A\) )、陽性になる( \(B\) )
- 病気ではなくて( \(A^{c}\) )、陽性になる( \(B\) )
この2つのパターンは同時には起こらないので、それぞれの確率を足し合わせれば \(P(B)\) が求まります。つまり、 \(P(B)=P(B∩A)+P(B∩A^{c})\) です。これを条件付き確率の式を使って変形すると、
\[
P(B) = P(B \mid A) \, P(A) + P(B \mid A^{c}) \, P(A^{c})
\]
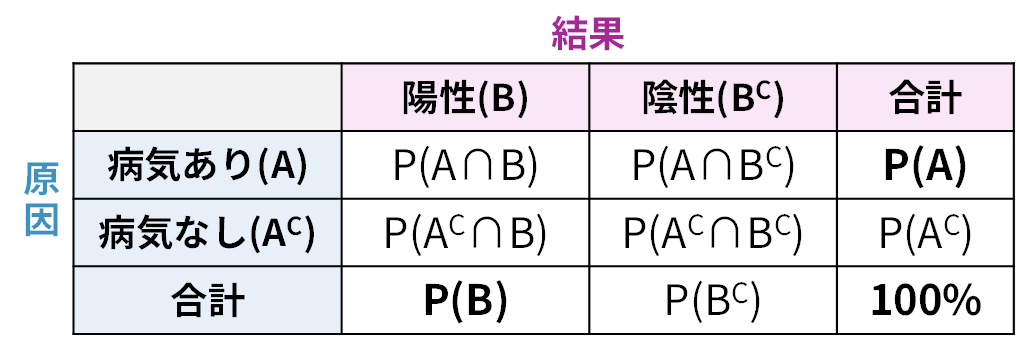
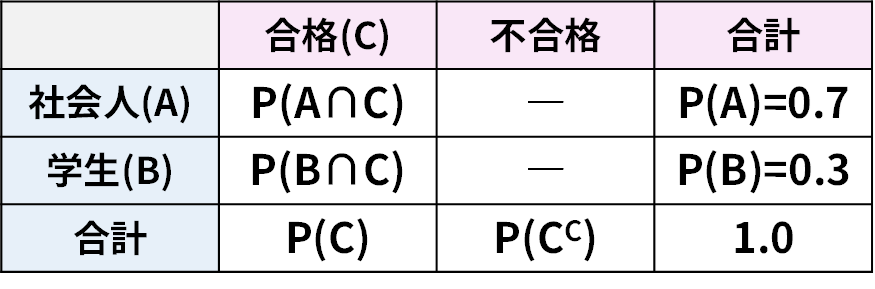
となります。ベイズの定理の公式の分母は、この形に分解して計算することがほとんどです。要は「陽性になる確率 = (病気の人が陽性になる確率) + (病気でない人が陽性になる確率)」という、当たり前のことを数式で表現しているだけです。※混乱したときは分割表(以下再掲)で整理することをおすすめします!

06. 確率変数
統計学では、さまざまな計算をするために、事象の結果に「確率」を割り当てて考えます。その便利な道具が確率変数(Random Variable)です。通常、 \(X\) や \(Y\) のような大文字で表されます。例えば、「サイコロを1回投げる」という試行において、出る目を表す確率変数を \(X\) とすると、 \(X\) は 1, 2, 3, 4, 5, 6 という値をとります。確率変数には大きく2種類あります。
- 離散確率変数:とる値が 1, 2, 3 のように「とびとび」で数えられるもの。(例:サイコロの目、コインを投げて表が出る回数)
- 連続確率変数:とる値が切れ目なく連続しているもの。(例:身長、体重、時間)
離散と連続の確率表現
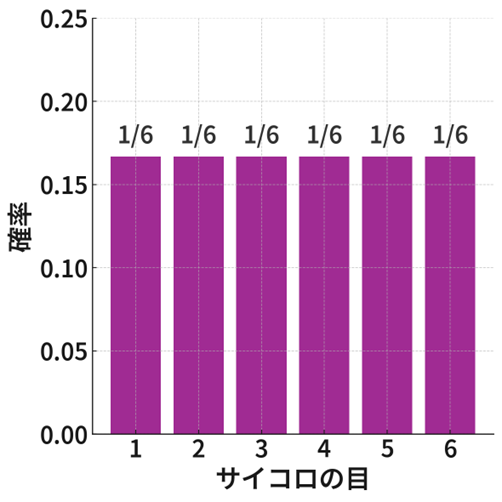
離散確率変数の場合、それぞれの値をとる確率を確率関数 \(P(X=x)\) で表します。例えば、普通のサイコロなら \(P(X=1)=1/6\) , \(P(X=2)=1/6\) , … となります。すべての確率を足すと、必ず1になります。
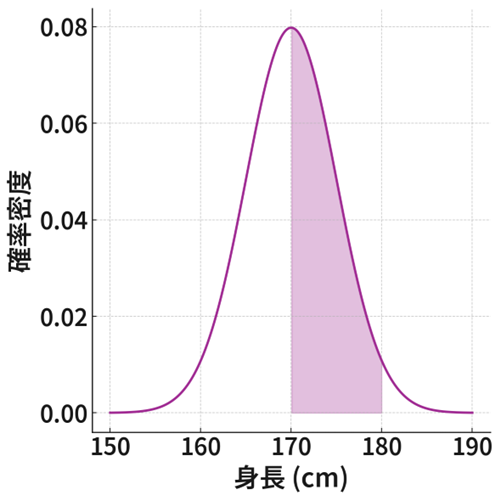
連続確率変数の場合は少し注意が必要です。身長が「ピッタリ170.000…cm」になる確率は、限りなく0ですよね。なので、連続型では \(P(X=x)=0\) となります。その代わり、確率密度関数 \(f(x)\) というグラフ(山の形などをしていることが多い。例:正規分布)を使い、そのグラフと \(x\) 軸で囲まれた面積が確率を表します。「身長が170cm以上180cm以下になる確率(下図の紫色で塗りつぶされた面積)」のように、範囲で確率を考えます。
07. 期待値と分散
確率変数がどのような値をとるかがわかったら、次はその変数全体の特徴を知りたくなります。その代表が期待値と分散です。
期待値 E[X]
期待値は、その確率変数が「平均してどのくらいの値をとるか」を示す指標です。「平均値」の確率バージョンだと思ってください。計算方法は、「(変数がとる値)×(その値をとる確率)」を、すべての値について足し合わせます。
\[
E[X] = \sum_{i} x_{i} \, P(X = x_{i})
\]
\(\sum\) (シグマ)記号は「全部足し合わせる」という意味です。例えば、例題の特殊なサイコロのように、1の目が3面、2の目が1面、3の目が2面あるサイコロを考えてみましょう。 \(P(X=1)=3/6\) 、 \(P(X=2)=1/6\) 、 \(P(X=3)=2/6\) となります。このときの期待値 \(E[X]\) は、

\[\begin{align*}
E[X]&= 1 \times \frac{3}{6}+ 2 \times \frac{1}{6}+ 3 \times \frac{2}{6} \\[6pt]
&= \frac{3 + 2 + 6}{6}= \frac{11}{6}
\end{align*}\]
となります。何度もサイコロを振れば、出る目の平均は 11/6(約1.83)に近づいていく、というわけです。
分散 V[X]
分散は、データの「ばらつき具合」を表す指標です。値が期待値(平均)の周りに密集しているのか、それとも広範囲に散らばっているのかを示します。分散は、「偏差(各データと期待値の差)の2乗の期待値」として定義されます。
\[
V[X] = E\!\left[(X – E[X])^2\right]
\]
つまずきポイント:
なぜ2乗するのか? それは、偏差 \((X-E[X])\) にはプラスもマイナスもあるため、そのまま平均すると打ち消し合って0に近づいてしまうからです。2乗することで、すべての偏差を正の値にして、ばらつきの大きさを正しく評価できるようにしているのです。
この定義式は少し計算が面倒なので、実務ではこちらの「2乗の期待値 – 期待値の2乗」という以下の公式がよく使われます。絶対に覚えましょう。
\[
V[X] = E[X^{2}] – (E[X])^{2}
\]
\(E[X^{2}]\) は、「 \(X\) の値を2乗したもの」の期待値です。先ほどの特殊なサイコロの例で計算すると、

\[\begin{align*}
E[X^{2}] &= 1^{2} \times \frac{3}{6} + 2^{2} \times \frac{1}{6} + 3^{2} \times \frac{2}{6} \\[6pt]
&= \frac{3 + 4 + 18}{6} = \frac{25}{6}
\end{align*}\]
となります。期待値は \(E[X]=11/6\) だったので、その2乗は \((11/6)^{2}=121/36\) です。よって、分散 \(V[X]\) は、
\[\begin{align*}
V[X] &= \frac{25}{6} – \frac{121}{36} \\[6pt]
&= \frac{150}{36} – \frac{121}{36} = \frac{29}{36}
\end{align*}\]
と計算できます。
08. 腕試し!模擬問題に挑戦
さて、ここまで学んだ知識を使って、以下の模擬問題に挑戦してみましょう。
【模擬問題1】
ある資格試験の受験者に占める社会人の比率は 0.7 であった。この試験の合格率は、社会人が 0.3、学生が 0.6 であった。
(1) この資格試験全体の合格率を求めよ。
(2) この試験の合格者の中からランダムに1人を選んだとき、その人が学生である確率を求めよ。
【模擬問題2】
ある工場では、製品の5%が不良品として製造される。この工場には、不良品を検出するための検査システムがあり、その性能は以下の通りである。
- 製品が本当に不良品の場合、95%の確率で「異常」と判定する。
- 製品が良品の場合でも、2%の確率で誤って「異常」と判定してしまう。
ある製品をこのシステムで検査したところ、「異常」と判定された。この製品が本当に不良品である確率を求めよ。
【模擬問題1の解説】
(1) 全体の合格率
これは、①「社会人かつ合格する確率」と②「学生かつ合格する確率」を足し合わせることで求められます(全確率の定理の考え方です)。
- 受験者が社会人である事象を \(A\) 、学生である事象を \(B\) 、合格する事象を \(C\) とする。
- \(P(A)=0.7\) なので、 \(P(B)=1-0.7=0.3\) となる。
- 社会人の合格率は「社会人であるという条件下で合格する確率」なので、 \(P(C \mid A)=0.3\) 。
- 学生の合格率は「学生であるという条件下で合格する確率」なので、 \(P(C \mid B)=0.6\) 。
① 社会人かつ合格する確率:
\(P(A∩C)=P(C \mid A)P(A)=0.3 \times 0.7=0.21\)
② 学生かつ合格する確率:
\(P(B∩C)=P(C \mid B)P(B)=0.6 \times 0.3=0.18\)
よって、全体の合格率は \(P(C)=0.21+0.18=0.39\) となります。
答え: \(0.39\)
(2) 合格者が学生である確率
これは「合格したという条件下で、その人が学生である確率」、つまり条件付き確率 \(P(B \mid C)\) を求める問題です。条件付き確率は以下の公式で計算します。
\[
P(B \mid C)=\frac{P(B∩C)}{P(C)}
\]
分子の \(P(B∩C)\) は(1)で計算した \(0.18\) です。分母の \(P(C)\) も(1)で計算した \(0.39\) です。よって、
\[
P(B \mid C) = \frac{0.18}{0.39} = \frac{18}{39} = \frac{6}{13}
\]
となります。
答え: \(6/13\)
【模擬問題2の解説】
これは典型的なベイズの定理の問題です。結果(「異常」と判定 )から原因(本当に不良品か)の確率を求めます。
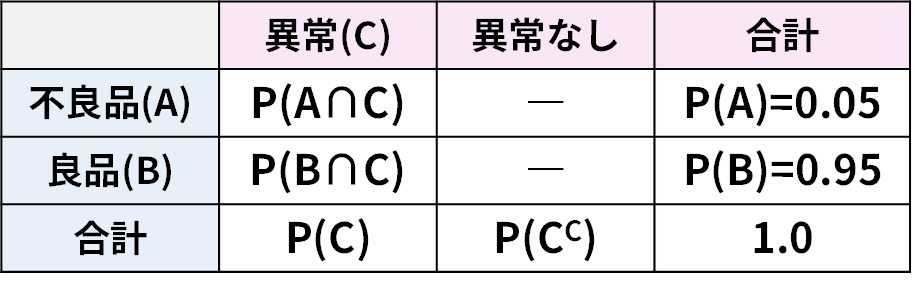
- 製品が不良品である事象を \(A\) 、良品である事象を \(B\) とする。
- 検査で「異常」と判定される事象を \(C\) とする。
問題文から情報を整理すると
- 事前確率: \(P(A)=0.05\)、 \(P(B)=1-0.05=0.95\)
- 条件付き確率:
- \(P(C \mid A)=0.95\) (不良品を正しく「異常」と判定する確率)
- \(P(C \mid B)=0.02\) (良品を誤って「異常」と判定する確率)
求めたいのは、「異常」と判定されたときに、それが本当に不良品である確率、つまり \(P(A \mid C)\) です。ベイズの定理の公式に当てはめましょう。
\[
P(A∣C)=\frac{P(C∣A)P(A)}{P(C)}
\]
まずは分母の \(P(C)\) を計算します。「異常」と判定されるのは、「不良品が異常と判定される」場合と「良品が異常と判定される」場合の2パターンです。
\[\begin{align*}
P(C)&= P(C \mid A) P(A) + P(C \mid B) P(B) \\[6pt]
&= (0.95 \times 0.05) + (0.02 \times 0.95) \\[6pt]
&= 0.0475 + 0.019 \ = 0.0665
\end{align*}\]
これで全てのパーツが揃いましたので、求めたい \(P(A \mid C)\) の式に代入すると
\[\begin{align*}
P(A∣C)&=\frac{P(C∣A)P(A)}{P(C)}\\[6pt]
&=\frac{0.95×0.05}{0.0665}=\frac{0.0475}{0.0665}\\[6pt]
&=\frac{475}{665}=\frac{95}{133}
\end{align*}\]
計算すると、約 \(0.714\) となります。検査で異常と出ても、本当に不良品である確率は約 \(71.4%\) ということですね。
答え:\(95/133\) (約 \(71.4%\) )
09. まとめ
お疲れ様でした!今回は統計検定準1級の土台となる「事象と確率」について、つまずきやすいポイントを中心に解説しました。
- 条件付き確率は、分母(考える世界)が変化するイメージを持つ。
- ベイズの定理は、結果から原因を探る強力なツール。分母の計算は「全パターンを足し合わせる」と考える。
- 確率変数は、事象の結果を「確率」というメガネを通して表現したもの。
- 期待値(平均)と分散(ばらつき)は、データ全体の特徴を掴むための基本指標。
これらの概念は、この先で学習する「確率分布」「推定」「検定」といった分野でも繰り返し登場します。ここでしっかりと基礎を固めておくことが、合格への一番の近道です。確率の問題は、文章を読んで状況を正しく整理し、どの公式を使うべきかを見極める「翻訳力」が試されます。たくさんの問題に触れて、ぜひ確率と仲良くなってください。次回もまた一緒にがんばりましょう!

