準1級文系解説｜第02回「確率分布と母関数」【限定公開】

準1級文系解説について（各回共通）

　ご訪問いただきありがとうございます。こちらは統計検定🄬準1級合格を目指す方が、公式テキスト『統計学実践ワークブック』やそのほか統計検定🄬準1級対策コンテンツをスラスラと学び進めるために必要な解説を行うブログです。
　本ブログは、公開されている「統計検定🄬準1級出題範囲」の各項目について執筆しています。「統計検定🄬準1級出題範囲」は『統計学実践ワークブック』の内容にも対応していますので、本ブログの解説が『統計学実践ワークブック』の読解に役立つ部分も多くあるかと思います。その意味で、本ブログをご覧いただく方には、公式テキスト『統計学実践ワークブック』を購入されることを推奨いたします。
　なお、統計検定🄬は一般財団法人統計質保証協会の登録商標です。また、本ブログは一般財団法人統計質保証協会から公認されたコンテンツではありません。

00. はじめに

　「同時確率密度関数」「モーメント母関数」、、、統計検定準1級のテキストを開くと、急に漢字や数式の羅列が激しくなり、心が折れそうになりませんか？ 特に「確率分布」の後半から登場するこれらのトピックは、多くの独学者が挫折するポイントです。

　でも、もし「確率分布のすべての情報が詰まった、たった１つの関数」が存在するとしたらどうでしょう？ 平均や分散はもちろん、その分布が持つ様々な性質を、まるでカプセルから取り出すように簡単に計算できるとしたら…？そんな魔法のようなツールが、今回学ぶ母関数（ぼかんすう）です。この記事を読み終える頃には、以下のような内容についての理解が深まっているはずです。

• 多変数への拡張：2つ以上の確率変数を同時に扱う「同時分布」「周辺分布」「条件付き分布」を使いこなす視点
• 確率分布の裏の顔：「累積分布関数」「生存関数」といった、分布を別の角度から表現する方法
• 最強の時短ツール：「確率母関数」「モーメント母関数」を自在に操り、面倒な期待値・分散計算を微分で簡単解決するテクニック
• 母関数の真の力：独立な確率変数の和の分布を、驚くほど簡単に導出できる性質の理解

　一見すると難解な数式も、その「意味」と「目的」を理解すれば、これほど頼りになる相棒はいないとも思えてくるかもしれません。それでは一緒に確率分布の世界を楽しみましょう！

この第02回「確率分布と母関数」の内容では数学的な話が多く登場します。読み解くのに苦労する部分もあるかもしれませんが、後の回でも必ず役に立つ内容です。ぜひここで踏ん張って、ひとつひとつの内容を読み進めていきましょう！

01. 同時確率分布

　これまでは、サイコロの目 (\(X\)) のように、1つの確率変数だけを見てきました。しかし、実社会の問題はもっと複雑です。例えば、「数学の点数 (\(X\)) 」と「英語の点数 (\(Y\)) 」のように、複数の変数が絡み合ってきます。

同時確率分布と周辺分布

　同時確率関数（離散）や同時確率密度関数（連続）は、確率変数 \(X\) と \(Y\) が「同時に」特定の値をとる確率や密度を表すものです。 \(P(X＝x, Y＝y)\) や \(f(x, y)\) のように書きます。2変数なので、平面上の表や、3Dの曲面グラフで表現されるイメージです。

つまずきポイント：

　ここで、最初の「つまずきポイント」が登場します。周辺分布です。名前が難しそうですが、意味は至ってシンプル。同時確率の表があったとき、「端っこ（margin）」に書く合計値のことです。例えば、 \(X\) と \(Y\) の同時確率関数が以下の表で与えられたとしましょう。

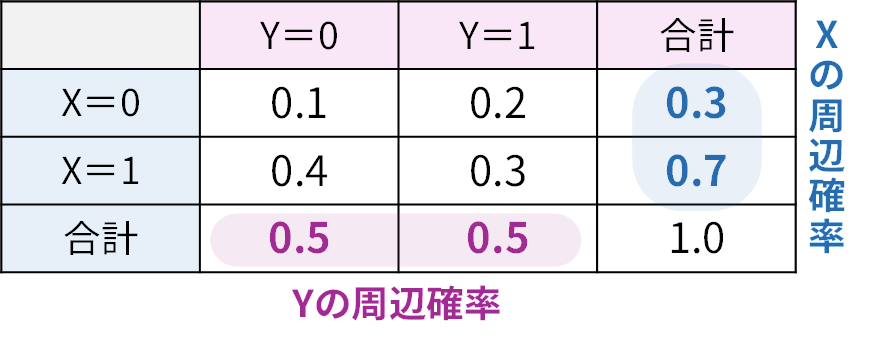
　この表の右端の合計欄（0.3, 0.7）が、 \(Y\) の値を無視した \(X\) だけの確率分布、つまり \(X\) の周辺確率関数です。同様に、下端の合計欄（0.5, 0.5）が \(Y\) の周辺確率関数となります。連続変数の場合は、この「合計する」という操作が積分に変わります。 \(X\) の周辺確率密度関数 \(f_X​(x)\) を求めたければ、同時確率密度関数 \(f(x, y)\) を \(Y\) について積分（合計）します。

\[
f_X(x) = \int_{-\infty}^{\infty} f(x,y) \, dy
\]

　この式は「ある \(x\) に固定したとき、 \(y\) がどんな値をとってもいいから、その確率密度を全部足し合わせて（積分して）、 \(x\) だけの確率密度を求めよう」というものです。この計算で少し偏微分や重積分の知識が必要になることがありますが、準1級では主に多項式や指数関数の基本的な計算がほとんどなので、過度に恐れる必要はありません。

条件付き分布

　これは第１回の復習です。 \(P(Y=y \mid X=x)\) は、「 \(X=x\) という条件（世界）の中で、 \(Y=y\) となる確率」でしたね。これは、同時確率を条件の確率で割ることで計算できます。

\[
P(Y = y \mid X = x) = \frac{P(X = x, \, Y = y)}{P(X = x)}
\]

　分母の \(P(X=x)\) は、まさに先ほど求めた \(X\) の周辺確率です。つまり、同時分布と周辺分布が分かっていれば、条件付き分布もすぐに計算できるというわけです。

02. 累積分布関数

　確率関数や確率密度関数は分布の基本ですが、実用上、別の形で分布を表現すると便利なことがあります。

累積分布関数（CDF）

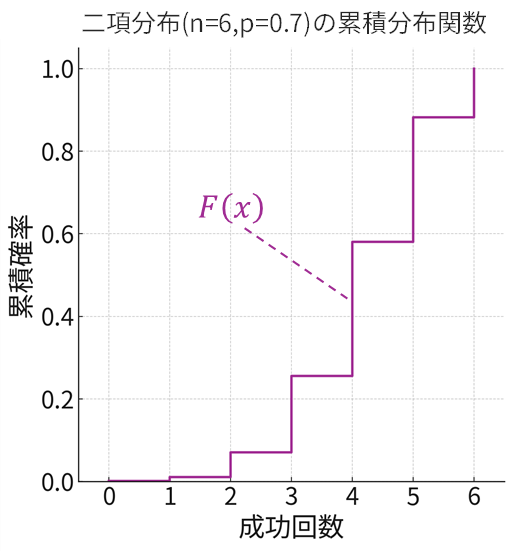
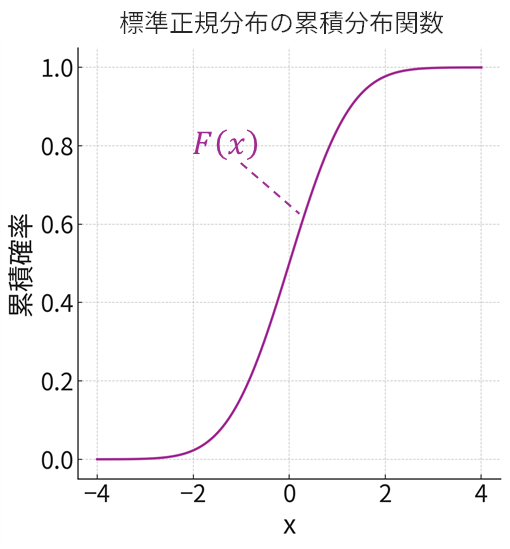
　累積分布関数（るいせきぶんぷかんすう）、英語でCumulative Distribution Function、略してCDFは、その名の通り確率を「累計」したものです。確率変数 \(X\) がある値 \(x\) 「以下」である確率、つまり \(F(x)=P(X≦x)\) を表します。例えば、二項分布（試行回数 \(n=6\) 、成功確率 \(p=0.7\) ）や標準正規分布の累積分布関数は以下のグラフで表されます。

つまずきポイント：

　「なぜこんなものが必要なの？」と思うかもしれませんが、累積分布関数には絶大なメリットがあります。

1. 離散も連続も同じ形で扱える：棒グラフと曲線グラフで形の違った確率（密度）関数と違い、累積分布関数はどちらも階段状またはなめらかな右上がりのグラフになり、統一的に議論できます。
2. 区間確率の計算が楽：例えば「 \(X\) が \(a\) より大きく \(b\) 以下である確率」 \(P(a<X≤b)\) は、累積分布関数を使えば単なる引き算 \(F(b)−F(a)\) で計算できます。いちいち積分計算をしなくて済むのです。

生存関数とハザード関数

　これらは特に、製品の寿命や生命保険の分野で活躍する関数です。

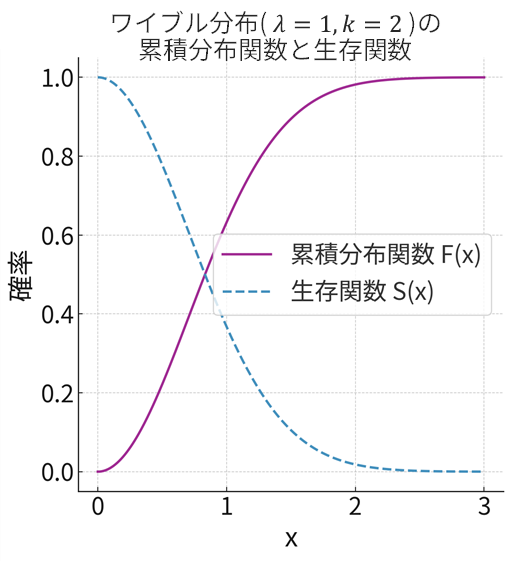
• 生存関数 \(S(x)\)：累積分布関数の真逆です。確率変数 \(X\) がある値 \(x\) を「超える」確率、 \(S(x)=P(X>x)\) を表します。累積分布関数が分かっていれば、 \(S(x)=1−F(x)\) ですぐに計算できます。「ある製品が \(x\) 年後も生き残っている（生存している）確率」と考えるとイメージしやすいですね。
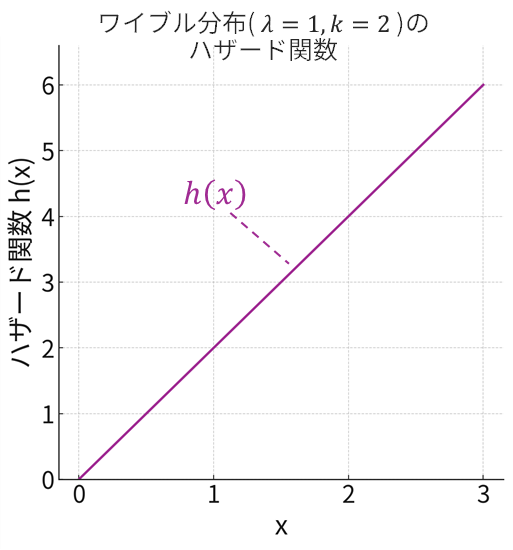
• ハザード関数 \(h(x)\)：これは少し高度な概念です。「ある時点 \(x\) まで生き残ったという条件の下で、その瞬間に故障（死亡）する確率密度」を表します。言い換えれば、「その瞬間のリスクの高さ」を示す関数です。車の走行距離が増えるほど故障リスクが上がるように、ハザード関数は時間と共に増加することが多いです。ハザード関数は、確率密度関数 \(f(x)\) を生存関数 \(S(x)\) で割ることで定義されます。\[h(x)=\frac{f(x)}{S(x)}=\frac{f(x)}{1-F(x)}\]

　例えば、ワイブル分布という確率分布においては、形状パラメータ \(k\) が \(k>1\) の場合、以下の下段グラフ（上段が累積分布関数と生存関数、下段がハザード関数）のようにハザード関数が時間とともに単調に増加します。これは「使い始めは壊れにくいが、長く使うほど故障リスクが高まる」といった状況をうまく表現するものです。

03. 母関数

　お待たせしました。いよいよ今回の主役、母関数（Generating Function）の登場です。母関数とは、確率分布のすべての情報（モーメント：期待値や分散など）を生成（generate）できる、いわば「親」となる関数です。主に3種類ありますが、準1級ではそのうち2つ（確率母関数、モーメント母関数）をしっかり押さえましょう。

確率母関数（PGF）

　確率母関数（Probability Generating Function, PGF）は、「0以上の整数値をとる離散確率変数」専用の母関数です。定義式は以下になります。

\[\begin{align*}
G(s) &= E[s^{X}] \\[4pt]
&= \sum_{k=0}^{\infty} P(X = k) \, s^{k}
\end{align*}\]

つまずきポイント：

　この数式を見て思考停止しないでください！これは「 \(s^{k}\) の係数が、確率 \(P(X=k)\) になっているような、 \(s\) の多項式です」と宣言しているだけです。例えば、

\[\begin{align*}
P(X=0)&=0.1,\\
P(X=1)&=0.2,\\
P(X=2)&=0.7
\end{align*}\]
なら、確率母関数は

\[\begin{align*}
G(s)&=0.1s^{0}+0.2s^{1}+0.7s^{2}\\
&=0.1+0.2s+0.7s^{2}
\end{align*}\]

となります。意外とシンプルですよね？

確率母関数(PGF)の微分で期待値・分散を求める

　この確率母関数の真骨頂は、微分と組み合わせることで発揮されます。ここでの計算は、一見すると複雑に見えますが、以下のルールさえ押さておけば大丈夫です。

ルール：期待値の微分

　確率母関数の定義は \(G(s)=E[s^{X}]\) でした。これを \(s\) で微分（ \(X\) ではなく \(s\) で微分です！）するとき、難しく考えず「微分記号 \( (’) \) は、期待値の記号 \(E\) の中に入り込める」と覚えてください。※証明が気になる方は数学の教科書等をぜひご覧ください（準1級に合格した後でも大丈夫です）

\[
\bigl(E[s^{X}]\bigr)’ = E\!\left[(s^{X})’\right]
\]

　そして、カッコの中の \( (s^{X})’ \) は、高校数学で習う \((x^{n})’ = n x^{\,n-1}\) と同じように、 \(X\) を定数のように扱って微分できます。

\[
(s^{X})’ = X \, s^{\,X-1}
\]

　つまり、このルールを適用すると、確率母関数の微分は以下のようになります。

\[\begin{align*}
G'(s) &= \bigl(E[s^{X}]\bigr)’ = E\!\left[X s^{\,X-1}\right]\\[4pt]
G^{\prime\prime}(s) &= E\!\left[X(X-1) s^{\,X-2}\right]
\end{align*}\]

　これが、母関数を使った計算のすべての出発点となる、最も重要な式変形です。というのも、このルールを踏まえれば、母関数から期待値や分散を導けるからなんですね。

• 期待値 \(E[X]\) ：確率母関数 \(G(s)\) を \(s\) で1回微分して、 \(s=1\) を代入すると求まります。
  \[G'(1)=E\!\left[X \times 1^{\,X-1}\right]=E[X]\]
• 分散 \(V[X]\) ：確率母関数 \(G(s)\) を2回微分したものと1回微分したものを整理すると
  \[\begin{align*}
  G^{\prime\prime}(1)+G^{\prime}(1)&= E\!\left[X(X-1)\right]+E[X]\\
  &=E[X^{2}]
  \end{align*}\]なので、分散 \(V[X]\) は分散の公式から以下のように導けます。
  \[\begin{align*}
  V[X]&=E[X^{2}]-\bigl(E[X]\bigr)^{2}\\
  &=G^{\prime\prime}(1)+G^{\prime}(1)-\bigl(G^{\prime}(1)\bigr)^{2}
  \end{align*}\]

　上記のように、面倒なシグマ計算をシンプルな微分計算に置き換えてしまう、まさに時短ツールです。

モーメント母関数（積率母関数・MGF）

　モーメント母関数（Moment Generating Function, MGF）は、離散・連続を問わず使える、より汎用性の高い母関数です。別名、積率母関数とも呼ばれます。定義式は以下のとおりです。

\[
M(\theta)=E[e^{ \theta X}]
\]

　離散なら \(\sum_{x=0}^{\infty} e^{ \theta x} \, P(X = x)\) 、連続なら \(\int_{-\infty}^{\infty} e^{ \theta x} f(x) \, dx\) を計算します。

モーメント母関数(MGF)の微分でモーメントを求める

　モーメント母関数 \(M(\theta)\) は、その名の通り、微分することで様々な次数のモーメント（積率） \(E[X^{k}]\) を生成します。ここでの計算でも微分が必要ですが、以下のルールを押さえておけば大丈夫です。

ルール：指数関数 \(e^{a \theta }\) の微分

　モーメント母関数の計算では、ネイピア数 \(e\) が登場する指数関数の微分が必須になります。数学の証明は不要ですが、以下の便利な公式だけここで押さえておきましょう。

\[
(e^{a \theta})’ = a e^{a \theta}
\]

　変数 \( \theta \) を含む指数関数 \(e^{a \theta }\) ( \(a\) は定数) を \( \theta \) で微分すると、肩に乗っている \( \theta \) の係数「\(a\)」が前にポンと出てくる、と覚えてください。例えば、 \(e^{3\theta}\) を \(\theta\) について微分すると \(3e^{3\theta}\) に、 \(e^{-5\theta}\) を \(\theta\) について微分すると \(-5e^{-5\theta}\) になります。とてもシンプルですよね！そして、このルールをモーメント母関数 \(M(\theta)\) に適用すると以下のように微分できます。ここでも \(X\) ではなく \(\theta\) で微分していることに注意しましょう。

\[\begin{align*}
M'(\theta)&=\bigl(E[e^{ \theta X}]\bigr)’=E[Xe^{\theta X}]\\[4pt]
M^{\prime\prime}(\theta)&=E[X^{2} e^{\theta X}]
\end{align*}\]

　上記のルールを踏まえれば、以下のようにモーメント母関数 \(M(\theta)\) からモーメント \(E[X^{k}]\) を導けます。

• モーメント母関数 \(M(\theta)\) を \(\theta\) で1回微分したものに \(\theta=0\) を代入すると、1次のモーメント \(E[X]\) （つまり期待値）が求まります。
  \[
  M'(0)=E[Xe^{0}]=E[X]
  \]
• モーメント母関数 \(M(\theta)\) を \(\theta\) で2回微分したものに \(\theta=0\) を代入すると、2次のモーメント \(E[X^{2}]\) が求まります。
  \[
  M^{\prime\prime}(0)=E[X^{2} e^{0}]=E[X^{2}]
  \]
• モーメント母関数 \(M(\theta)\) を \(\theta\) で \(k\) 回微分したものに \(\theta=0\) を代入すると、 \(k\) 次のモーメント \(E[X^{k}]\) が求まります。
  \[
  M^{(k)}(0)=E[X^{k} e^{0}]=E[X^{k}]
  \]
  

　なお、分散はおなじみの公式 \(V[X]=E[X^{2}]-(E[X])^{2}\) を使って以下のように導けます。

\[\begin{align*}
V[X]&=E[X^{2}]-\bigl( E[X] \bigr)^{2}\\[4pt]
&=M^{\prime\prime}(0)-\bigl( M'(0) \bigr)^{2}
\end{align*}\]

　つまり、モーメント母関数 \(M(\theta)\) がわかっていれば、それを微分することによって、期待値や分散を導出することができるのです。

特性関数（参考）

　モーメント母関数（MGF）はとても便利な道具ですが、分布によっては「計算していくと数値が無限大にふくらんでしまい、有限の答えに落ち着かない（＝収束しない）」ことがあります。そうなると、モーメント母関数という仕組み自体が成り立たず「存在しない」ことになってしまいます。

　そんなときでも必ず使えるのが特性関数です。これは \(E[e^{i \theta X}]\) と定義され、 \(i\) は「2乗すると-1になる不思議な数（虚数単位）」です。ポイントは、 \(e^{i \theta X}\) という数は「大きさ（絶対値）が常に1」であることです。つまり、どんな分布でも値が暴走して無限大にふくらむことはなく、必ず落ち着いた形で存在します。

　準1級の試験では計算問題として出ることはほとんどありませんが、「モーメント母関数よりも”タフ”で、どんな場合にも必ず成り立つ母関数がある」と知っておくと安心です。

母関数のすごい性質

　さらに、母関数には2つの重要な性質があります。

1. 確率分布との1対1対応：ある確率分布の母関数は、ただ1つに決まります。逆に、ある母関数の形を見れば、それがどんな確率分布から生まれたのかを特定できます。
2. 独立な変数の和は、母関数の積： これが極めて重要です！ 独立な確率変数 \(X\) と \(Y\) があるとき、その和 \(Z=X+Y\) の母関数は、それぞれの母関数の積になるのです。ただし、\(X\) と \(Y\) が互いに独立であることが条件となることに注意してください。証明は本節の末尾に記載しました。
   \[\begin{align*}
   G_{Z}(\theta) &= G_{X}(\theta) \, G_{Y}(\theta)\\[4pt]
   M_{Z}(\theta) &= M_{X}(\theta) \, M_{Y}(\theta)
   \end{align*}\]
   　例えば、成功確率 \(p\) のベルヌーイ分布（1回試行）の確率母関数は以下のように導けます。
   \[
   \begin{align*}
   G(s) &= E[s^{X}] \\ &= (1-p)s^{0} + p s^{1} \\ &= (1-p) + ps
   \end{align*}
   \]
   　これを \(n\) 回繰り返した二項分布は、独立なベルヌーイ分布の和と考えられます。したがって、二項分布の確率母関数は、ベルヌーイ分布の確率母関数を \(n\) 個掛け合わせることで以下のように導けるのです。
   \[
   \{G(s)\}^{n}=\{(1-p)+ps\}^{n}
   \]
   　本来なら複雑な計算が必要な和の分布を、シンプルな掛け算で求めることができます。これが母関数の真の力です！なお、上記の導出をモーメント母関数で行う場合は以下のようになります。
   \[
   \begin{align*}
   M(\theta)&=E[e^{\theta X}]\\[3pt]
   &=(1-p)e^{0}+pe^{\theta}\\[3pt]
   &=(1−p)+pe^{\theta}\\[6pt]
   \Rightarrow \{M(\theta)\}^{n}&=\{(1−p)+pe^{\theta}\}^{n}
   \end{align*}
   \]

　独立な変数の和の確率母関数が、確率母関数の積となることの証明は以下のとおりです（モーメント母関数の場合も同様）。なお、繰り返し期待値の法則については次回テーマにてご紹介する予定です。
\[\begin{align*}
G_Z(\theta) &= E[\theta^{X+Y}] = E[\theta^X \theta^Y] \\[6pt]
&= E\,\big( E[\theta^X \theta^Y \mid X] \big) \quad \text{（繰り返し期待値の法則より）} \\[6pt]
&= E\,\big( \theta^X \,E[\theta^Y \mid X] \big) \\[6pt]
&= E\,\big( \theta^X \,E[\theta^Y] \big) \quad \text{（$X$と$Y$は独立なので）} \\[6pt]
&= E[\theta^X] \, E[\theta^Y] \\[6pt]
&= G_X(\theta)\,G_Y(\theta).
\end{align*}\]

04. 腕試し！模擬問題に挑戦

　それでは母関数の威力を体感してみましょう！

【模擬問題1】

　確率変数 \(X\) がパラメータ \(\lambda\) のポアソン分布にしたがうとする。ポアソン分布の確率関数は以下の式で与えられる。
\[
P(X = k) = \frac{\lambda^{k} e^{-\lambda}}{k!}, \quad k = 0,1,2,\ldots
\]
(1) \(X\) の確率母関数 \(G(s)=E[s^{X}]\) を求めよ。
（ヒント：以下の「マクローリン展開」呼ばれる式展開を利用します）
\[
e^{x} = \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\]
(2) 確率母関数を微分することにより、 \(X\) の期待値と分散を求めよ。

【模擬問題2】

　確率変数 \(X\) が区間 \([0, a]\) （ただし \(a>0\) ）の連続一様分布にしたがうとする。確率密度関数は \(f(x)=1/a​ \; (0≤x≤a)\) 、それ以外の \(x\) では \(f(x)=0\) である。
(1) \(X\) のモーメント母関数 \(M(\theta)\) を求めよ。
(2) 区間 \([0,1]\) の連続一様分布にしたがう確率変数 \(Y\) のモーメント母関数 \(M_{Y}(\theta)\) 、および、区間 \([0,2]\) の連続一様分布にしたがう確率変数 \(Z\) のモーメント母関数 \(M_{Z}(\theta)\) を求めよ。

【模擬問題1の解説】

(1) 確率母関数 \(G(s)\)
　定義式 \(G(s) = \sum_{k=0}^{\infty} s^{k} P(X = k)\) にポアソン分布の確率関数を代入します。
\[
\begin{align*}
G(s) &= \sum_{k=0}^{\infty} s^{k} \, \frac{\lambda^{k}}{k!} e^{-\lambda} \\[4pt]
&= e^{-\lambda} \sum_{k=0}^{\infty} \frac{(s\lambda)^{k}}{k!}
\end{align*}
\]
　ここで、指数関数 \(e^{x}\) のマクローリン展開 \(\sum_{k=0}^{\infty} \frac{x^{k}}{k!}\)​ を、 \(x=s\lambda\) として用いると
\[
G(s) = e^{-\lambda} e^{s\lambda} = e^{\lambda (s-1)}
\]

答え： \(G(s)=e^{\lambda (s-1)}\)

(2) 期待値と分散
　まず、 \(G(s)\) を \(s\) で微分します。
\[\begin{align*}
G'(s)&=\lambda e^{\lambda (s−1)}\\
G^{\prime\prime}(s)&=\lambda^{2} e^{\lambda(s−1)}
\end{align*}\]
　期待値は \(G'(1)\) なので、 \(E[X]=G'(1)=\lambda e^{0}=\lambda\) となります。また、分散は \(V[X]=G^{\prime\prime}(1)+G'(1)-(\{G'(1)\}^{2}\) なので、以下のように導けます。
\[
V[X]=\lambda^{2} e^{0}+\lambda-\lambda^{2}=\lambda
\]

答え：期待値 \(\lambda\) 、分散\(\lambda\)

【模擬問題2の解説】

(1) モーメント母関数 \(M(\theta)\)
　定義式 \(M(\theta) = \int_{-\infty}^{\infty} e^{\theta x} f(x) \, dx\) に一様分布の確率密度関数を代入します。積分範囲は \([0, a]\) だけで考えればOKです。
\[\begin{align*}
M(\theta) &= \int_{0}^{a} e^{\theta x} \frac{1}{a} \, dx \\[4pt]
&= \frac{1}{a} \left[ \frac{1}{\theta} e^{\theta x} \right]_{0}^{a} = \frac{1}{a \theta} \left(e^{a \theta} – e^{0}\right) \\[4pt]
&= \frac{e^{a \theta} – 1}{a \theta}
\end{align*}\]
※なお、上記式の2つ目の「＝」は通常の積分の計算展開になりますが、積分がまったくの初めての方は難しいかもしれません。別途積分の入門記事も公開したいと思いますが、以下の外部サイト様の記事がわかりやすいので、こちらもぜひご覧ください。　

積分の計算｜統計学の時間（外部サイトのページが開きます）

​答え： \(M(\theta)=\dfrac{e^{a \theta} – 1}{a \theta}\) ​

(2) 確率変数 \(Y,\; Z\) のモーメント母関数
　(1)で求めた区間 \([0,a]\) のときのモーメント母関数を用いて導くことができます。確率変数 \(Y\) の区間は \([0,1]\) なので \(a=1\) を代入すれば \(M_{Y}(\theta)\) を導くことができ、確率変数 \(Z\) の区間は \([0,2]\) なので \(a=2\) を代入すれば \(M_{Z}(\theta)\) を導くことができます。
\[\begin{align*}
M_{Y}(\theta)&=\frac{e^{\theta} – 1}{\theta}\\[6pt]
M_{Z}(\theta)&=\frac{e^{2\theta} – 1}{2\theta}
\end{align*}\]

こちらの問題について、本当は前問(1)で導いたモーメント母関数を用いて期待値と分散を導出する問題にしようと考えていました。しかし、それを解くためには「商の微分公式」や「ロピタルの定理」という応用的な知識が複数必要になりそう…ということで見送りました。統計検定🄬準1級としての対策を優先し、数学的な内容は統計検定🄬1級に譲ることにしましょう。

05. まとめ

　ここまでお疲れ様でした！今回は確率分布の世界を大きく広げ、そしてそれを効率的に扱うための「母関数」という強力なツールを学びました。

• 同時分布を見たら、まずは周辺分布（合計）を意識する。
• 累積分布関数は確率の「累計」、生存関数はその逆。
• 母関数は分布の情報を「カプセル化」したもの。微分すれば期待値や分散を簡単に導ける（ことが多い）。
• 独立な変数の和の母関数は、母関数の積で求められる。

　母関数は、その見た目の複雑さから敬遠されがちですが、一度理解しておけば、これほど頼もしい味方はいません。特に、さまざまな確率分布の期待値や分散を忘れてしまったときでも、母関数さえ覚えていれば自力で導出できるようになります。何度も繰り返し練習して、ぜひこの最強の時短ツールを自分のものにしましょう！