
準1級文系解説について(各回共通)
ご訪問いただきありがとうございます。こちらは統計検定🄬準1級合格を目指す方が、公式テキスト『統計学実践ワークブック』やそのほか統計検定🄬準1級対策コンテンツをスラスラと学び進めるために必要な解説を行うブログです。
本ブログは、公開されている「統計検定🄬準1級出題範囲」の各項目について執筆しています。「統計検定🄬準1級出題範囲」は『統計学実践ワークブック』の内容にも対応していますので、本ブログの解説が『統計学実践ワークブック』の読解に役立つ部分も多くあるかと思います。その意味で、本ブログをご覧いただく方には、公式テキスト『統計学実践ワークブック』を購入されることを推奨いたします。
なお、統計検定🄬は一般財団法人統計質保証協会の登録商標です。また、本ブログは一般財団法人統計質保証協会から公認されたコンテンツではありません。
00. はじめに
目の前に、テストの点数や商品の売上といった、大量のデータがあるとします。このデータの山から、私たちは何を知りたいでしょうか?おそらく、「平均はどのくらい?」「ばらつきは大きい?」「形は歪んでいる?」といった、データ全体を要約する特徴でしょう。
そんなデータの特徴を、いくつかの数値にぎゅっと要約してくれる便利な道具が「分布の特性値」です。これは、いわばデータの性質を伝えるニュースの見出しのようなものです。複雑なデータも、特性値を使えばその「アウトライン」がはっきりと見えてきます。この記事を通して、データ分析の基本にして王道とも言える、以下のテクニックを学んでいきましょう。
- 「平均」の使い分け:普通の平均だけではない、状況に応じて最適な武器(加重平均、幾何平均、調和平均)を選ぶ方法
- データの「形」を読み解く:平均や分散のさらに先へ、分布の歪み(歪度)や尖り(尖度)を理解する視点
- 「関係性」の罠を見抜く:2つの変数の関係(共分散・相関係数)を測り、「見せかけの相関」に騙されないための知識
- 計算の「法則」を使いこなす:面倒な計算をショートカット!期待値や分散に関する強力な法則をマスターするテクニック
基本的には2級の復習となります。しかし、準1級では「条件付き」の計算に慣れておく必要があったり、多次元へと拡張する方法(確率ベクトル)を理解しておく必要もあります。特に、多次元拡張の話はベクトルや行列が登場し苦手意識を持つ人も多いかと思います。ですが、ひとつひとつは決して難しくありませんので、焦らずにじっくりと要点をおさえていきましょう。
01. 単変量の特性値
まずは、1種類のデータ(例えば、クラスの生徒の身長)が持つ特徴を捉える方法を見ていきましょう。
いろいろな「平均」:「データの中心」はどこ?
平均と聞くと、全部足した合計をデータの数で割る算術平均が思い浮かびますよね。しかし、状況によっては他の平均を使った方が、より実態を正確に表せることがあります。
- 加重平均 (Weighted Average):「重要度」が異なるデータを平均するときに使います。例えば、大学の「成績(GPAなど)」を計算するとき、2単位の科目と4単位の科目では、4単位の科目の成績の方が重要ですよね。このように、各データの「重み」を考慮して計算するのが加重平均です。分子を「重みを掛け合わせた値の合計」とし、分母を「重みの合計」として計算します。
\[
\dfrac{(\text{値}_1 \times \text{重み}_1) + (\text{値}_2 \times \text{重み}_2) + \cdots}{\text{重み}_1 + \text{重み}_2 + \cdots}
\]
例えば、「経済学(2単位)」、「社会学(2単位)」、「法学(4単位)」の評定(100点満点)がそれぞれ「90点」、「80点」、「50点」であったとします。このとき、各科目の単位数を重みとした評定の加重平均は以下のように計算されます。
\[\begin{align*}
&\dfrac{(90\times2)+(80\times2)+(60\times4)}{2+2+4}\\[6pt]
&=\dfrac{180+160+240}{8}=72.5
\end{align*}\] - 幾何平均 (Geometric Mean):「成長率」や「変化率」といった、掛け算で変化していくものの平均を求めるときに使います。例えば、ある商品の売上が3年間で1.5倍、1.2倍、1.8倍になったとします。このときの平均的な成長率を計算するのに適しています。具体的には、3個の値(1.5倍、1.2倍、1.8倍)をすべて掛け合わせ、その3乗根をとります。
\[
\sqrt[3]{1.5 \times 1.2 \times 1.8 \rule{0pt}{0.8em}}\\
=(1.5 \times 1.2 \times 1.8)^{\tfrac{1}{3}}
\]
一般的には、 \(n\) 年間における各年の倍率を \(r_{1}, r_{2}, \cdots ,r_{n}\) として、以下のように整理できます。
\[
\sqrt[n]{r_{1} \times r_{2} \times \cdots \times r_{n} \rule{0pt}{0.8em}}\\
=(r_{1} \times r_{2} \times \cdots \times r_{n})^{\tfrac{1}{n}}
\] - 調和平均 (Harmonic Mean):「割合の平均」を計算するとき、とりわけ、「時速〇km」のような単位あたりの量(率)を平均するときに用いられる平均です。最もイメージが湧きにくい平均ですが、「往復の平均時速」の問題が典型例です。行きが時速30km、帰りが時速60kmのとき、平均時速は30と60を単純に平均して時速45km…とはなりません。正しい平均時速は以下の調和平均の式で計算できます。
\[\begin{align*}
\frac{2}{\tfrac{1}{30} + \tfrac{1}{60}}
&= \frac{2}{\tfrac{2+1}{60}}\\[6pt]
&= \frac{2}{\tfrac{3}{60}} = 40 \end{align*}\]
調和平均の計算式は一般化して表現すると少々ややこしくなります。いま「 \(n\) 個の値 \(x_{1}\), \(x_{2}\), \( \cdots , x_{n}\) 」があったとき、この調和平均は以下のような式で表せます。端的にいうと「逆数の平均の逆数」です。
\[
\frac{n}{\displaystyle \sum_{i=1}^{n} \frac{1}{x_i}}
\]
変動係数:「データのばらつき」をどう見る?
データのばらつき具合は、分散や標準偏差で測れます。しかし、これらには弱点があります。それは「単位や平均値が違うもの同士を比較できない」ことです。例えば、「ゾウの体重の標準偏差100kg」と「ネコの体重の標準偏差1kg」、どちらが「よりばらついている」と言えるでしょうか?絶対的な値ではゾウですが、平均体重を考えるとネコの方が相対的にばらついているかもしれません。そこで登場するのが以下の変動係数 (Coefficient of Variation, CV)です。
\[
\text{変動係数(CV)}=\frac{\text{標準偏差}}{\text{平均値}}
\]
変動係数は、平均値に対する標準偏差の割合を示すことで、単位や尺度の影響を取り除きます。これにより、「ゾウの体重」と「ネコの体重」のような、平均値が全く異なるグループのばらつき度合いを公平に比較できるようになります。

歪度と尖度:「データの形」はどんな形?
分布の形は、正規分布のような綺麗な釣鐘型だけではありません。その「形」の特徴を捉えるのがモーメントという概念です。モーメントは分布の形を数値で要約する道具とも言えるもので、「 \(r\) 次モーメント(原点まわりのモーメント)」と「 \(r\) 次中心モーメント」と呼ばれるものがあります。「 \(r\) 次モーメント(原点まわりのモーメント)」は以下のように定義されます。
\[
\mu_r’=E[X^{r}]
\]
例えば、 \(r=1\) のとき(1次モーメント)は \(E[X]\) となり、これは期待値(平均)そのものとなります。また、 \(r=2\) のとき(2次モーメント)は \(E[X^{2}]\) となります。
一方で、「 \(r\) 次中心モーメント」は以下のように定義されます。
\[
\mu_r=E\bigl[(X – \mu)^r\bigr]
\]
こちらは期待値からのズレを考慮したモーメントです。例えば、 \(r=3\) のとき(3次中心モーメント)は \(E\bigl[(X – \mu)^3\bigr]\) となり、これが歪度と呼ばれる指標のベースとなります。また、 \(r=4\) のとき(4次中心モーメント)は \(E\bigl[(X – \mu)^4\bigr]\) となり、これが尖度と呼ばれる指標のベースとなります。
歪度と尖度についての定義式を確認する前に、それぞれの意味やイメージを先に整理しておきましょう。
- 歪度 (Skewness):分布が左右対称からどれだけ「歪んでいるか」を示す指標です。
- 正の歪度:グラフの裾が右に長く伸びている形。平均値が中央値より右に来ます。(例:所得分布)
- 負の歪度:グラフの裾が左に長く伸びている形。平均値が中央値より左に来ます。(例:簡単なテストの点数分布)
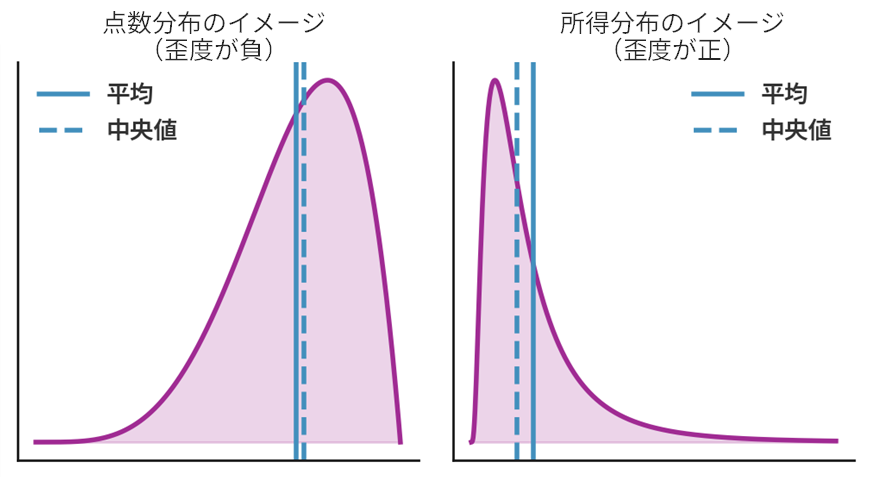
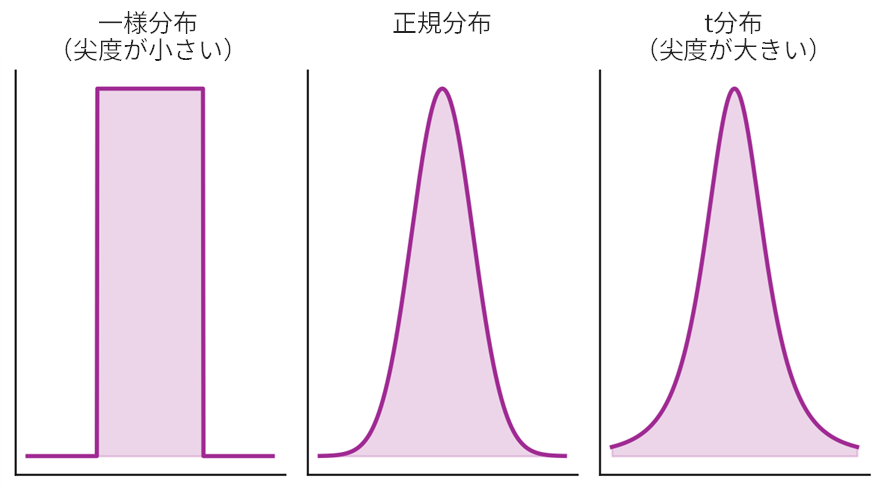
- 尖度 (Kurtosis):分布の山の「尖り具合」と、裾の「厚さ(太さ・重さ)」を示す指標です。正規分布と比べて、
- 尖度が大きい:山がより鋭く尖り、裾が厚い(=極端な値、つまり外れ値が発生しやすい)ことを意味します。
- 尖度が小さい:山がより平べったく、裾が薄い(=外れ値が発生しにくい)ことを意味します。
歪度と尖度の定義:数式で理解を深める
歪度と尖度は、期待値を使って以下のように定義されます。パーツごとに分解して「何をしているか」を理解しましょう。
歪度の定義式
\[
\text{歪度} = E\!\left[ \left( \frac{X – \mu}{\sigma} \right)^{3} \right]
\]
この式は、以下のステップで計算していることを意味します。
- 各データ点が平均 \(\mu\) からどれだけ離れているか(偏差: \(X-\mu\) )を計算します。
- その偏差を標準偏差 \(\sigma\) で割ることで、単位の影響をなくします(標準化: \((X-\mu)/\sigma\) )。「平均から標準偏差の何個分だけ離れているか」を示します。
- 標準化した値( \((X-\mu)/\sigma\) )を3乗します。ここがポイントです。「3(奇数)」乗ですので、元の偏差のプラス・マイナスの符号が保存されます。
- 最後にその3乗した値の期待値(平均)をとります。
つまり、もし分布の裾が右に長く伸びていれば(正の歪度)、標準化した値において非常に大きなプラスの値がたくさん生まれ、全体の平均(期待値)がプラスに引っ張られます。逆に左に長ければ、標準化した値において非常に小さなマイナスの値がたくさん生まれ、全体の平均(期待値)がマイナスに引っ張られます。左右対称なら、プラスとマイナスが打ち消し合って0に近くなる、という仕組みです。
尖度の定義式
\[
\text{尖度} = E\!\left[ \left( \frac{X – \mu}{\sigma} \right)^{4} \, \right] – 3
\]
こちらも同様に「何をしているか」をみてみましょう。
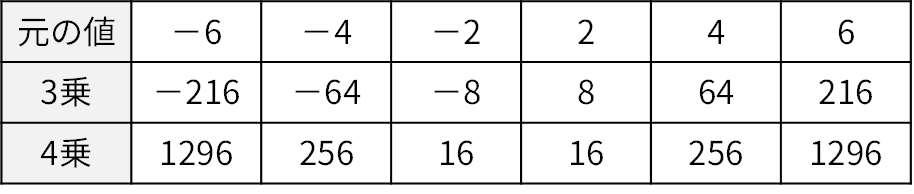
- 歪度と違って標準化した値を4乗しています。4乗するとすべての値がプラスになります。そして何より、平均から離れた値(外れ値)の影響が劇的に大きくなります。例えば、標準偏差2個分離れた値は \(2^{4}=16\) 、3個分離れた値は \(3^{4}=81\) もの大きさで全体の平均に貢献します。
- 最後に「3」を引いています。なぜ3なのか?というと、これは正規分布の尖度がちょうど3になるからです。つまり、基準である正規分布の尖度を0にするために、あらかじめ3を引いているのです。これを超過尖度と呼びます。
つまり尖度とは、「分布の裾の重さ(外れ値の多さ)が、正規分布と比べてどのくらいか」を敏感に測る指標なのです。プラスなら正規分布より裾が重く(外れ値が多く)、マイナスなら裾が軽い(外れ値が少ない)と解釈できます。
分位点関数:「データの中での位置」を知る
累積分布関数 (CDF) が「値 \(x\) 以下のデータは全体の何%か?」を教えてくれるのに対し、分位点関数 (Quantile Function) はその逆とも言える以下のような問いに答えます。
- 「データの下位90%に相当する値は?」
- 「上位10%に入るにはどのくらいの値が必要か?」
- 「分布の上側(値の大きい側)5%に対応する値は?」
このように、指定した割合(パーセント)を満たす値を返すのが分位点関数です。累積分布関数の逆関数の関係にあり、四分位数やパーセンタイルを計算する際に使われます。
- パーセンタイル (Percentile) :データを小さい順に並べたとき、下から数えて特定の位置(パーセント)にある値を指します。「90パーセンタイル」と言えば、下から数えて90%の位置にある値のことで、これより小さいデータが全体の90%を占めることを意味します。
- 四分位数 (Quartile) :パーセンタイルの中でも特に重要なのが、データを4等分する位置にある値、つまり四分位数です。
- 第1四分位数 (Q1):25パーセンタイルのこと。
- 第2四分位数 (Q2):50パーセンタイルのことで、これは中央値(メジアン)と同じです。
- 第3四分位数 (Q3):75パーセンタイルのこと。
「逆関数」とは?
難しく考える必要はありません。「逆関数」とは、元の関数の入力( \(x\) )と出力( \(y\) )を入れ替えたものです。
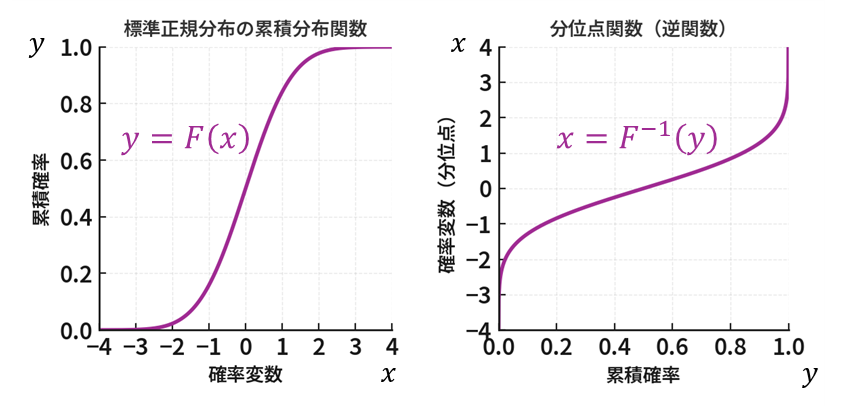
- 元の関数 (累積分布関数):値 \(x\) を入力すると、それが分布の下から何%の位置にあるかという確率 \(y\) を出力する。「値 \(x\) ⇒ 確率 \(y\) 」
\[ y=F(x) \] - 逆関数(分位点関数):確率 \(y\) を入力すると、分布における下からのその確率に対応する値 \(x\) を出力する。「確率 \(y\) ⇒ 値 \(x\) 」(しばしば以下のように関数の記号に \(-1\) を付して表す)
\[ x=F^{-1}(y) \]
02. 2変量の特性値
次に、「身長」と「体重」のように、2つ以上のデータがどのように関係しているかを示す特性値を見ていきましょう。
共分散と相関係数:「一緒に動く」度合いを測る
- 共分散 (Covariance):2つの変数が一緒に動く傾向を測る指標です。
- 共分散が正:片方が増えるとき、もう片方も増える傾向がある(例:身長と体重)。
- 共分散が負:片方が増えるとき、もう片方は減る傾向がある(例:勉強時間とゲーム時間)。
- 共分散は値の大きさに意味がありません。「共分散が100」と「共分散が5」のどちらが強い関係か、これだけでは判断できません。
- 相関係数 (Correlation Coefficient):共分散の弱点を克服したのが相関係数です。共分散を各変数の標準偏差で割ることで、値を常に-1から1の間に正規化します。
- 1に近い:強い正の相関
- -1に近い:強い負の相関
- 0に近い:ほとんど相関がない
- 相関係数を用いることで、データ間の関係の強さを同じ土俵で比較できます。
共分散と相関係数の定義式
それでは、これらの指標が数式の上でどのように定義され、なぜ「関係性」を測れるのか、その仕組みを確認しましょう。
共分散の定義式
変数 \(X\) の期待値を \(\mu_{X}\) 、変数 \(Y\) の期待値を \(\mu_{Y}\) とするとき、 \(X\) と \(Y\) の共分散 \(\mathrm{Cov}(X,Y)\) は以下の式で定義されます。
\[
\mathrm{Cov}(X,Y) = E\!\left[ (X – \mu_{X})(Y – \mu_{Y}) \right]
\]
この式が何をしているのか、パーツに分解して見ていきましょう。
- \((X – \mu_X)\):変数 \(X\) が、自身の平均からどれだけ離れているか( \(X\) の偏差)。
- \((Y – \mu_Y)\):変数 \(Y\) が、自身の平均からどれだけ離れているか( \(Y\) の偏差)。
- \((X – \mu_X)(Y – \mu_Y)\):上記2つの偏差を掛け合わせて偏差の積を計算します。この「偏差の積」をとることが共分散の一番のポイントです。
- 最後にこの偏差の積の期待値(平均)をとります。
散布図で確認してみましょう。平均(期待値)の線で区切られた4つの領域があります。それぞれの領域における「偏差の積」に着目すると、以下のように整理できます。
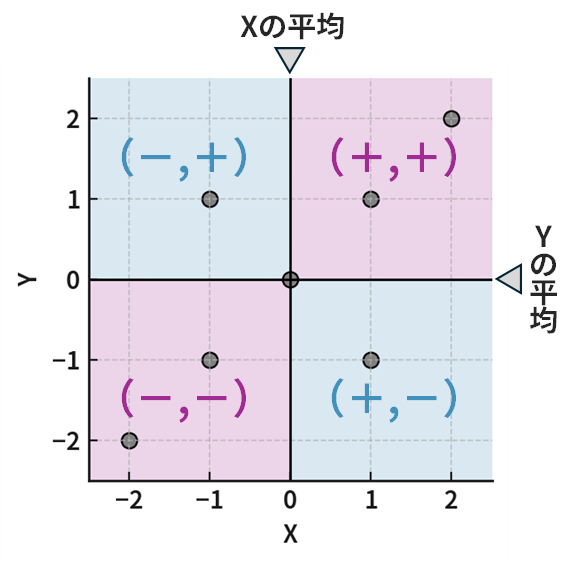
- 右上の領域: \(X\) も \(Y\) も平均より大きい(偏差は+, +)。偏差の積はプラス(+)。
- 左下の領域: \(X\) も \(Y\) も平均より小さい(偏差は-, -)。偏差の積はプラス(+)。
- 左上と右下の領域:片方がプラスで片方がマイナス。偏差の積はマイナス(-)。
つまり、もし多くのデータが「右上と左下の対角領域」にあれば、プラスの「偏差の積」が多くなり、共分散は正の値をとりやすくなります。逆に「左上と右下の対角領域」にデータが多ければ、マイナスの「偏差の積」が多くなり、共分散は負の値をとりやすくなります。そして、データが4つの領域にまんべんなく散らばっていれば、プラスとマイナスが打ち消し合って共分散は0に近くなります。
相関係数の定義式
変数 \(X\) の標準偏差を \(\sigma_{X}\) 、変数 \(Y\) の標準偏差を \(\sigma_{Y}\) とするとき、 \(X\) と \(Y\) の相関係数 \(\rho_{X,Y}\) (「\(\rho\)」はギリシャ文字で「ロー」と読みます)は以下の式で定義されます。
\[
\rho_{XY} = \frac{\mathrm{Cov}(X,Y)}{\sigma_X \, \sigma_Y}
\]
この式は、先ほど計算した共分散を、各変数の標準偏差(\(\sigma_X, \sigma_Y\))の積で割っているだけです。
なぜ、このようなことをするのでしょうか?それは、共分散が持つ「単位に影響されてしまう」という弱点を克服するためです。例えば、身長と体重の共分散を計算するとき、身長をメートルで測るかセンチメートルで測るかで、共分散の値は100倍も変わってしまいます。これでは関係の「強さ」を客観的に評価できません。
そこで、それぞれの標準偏差で割る(標準化する)ことで、単位の影響を完全に消し去ります。これにより、どんなデータでも必ず \(-1\) から \(+1\) の範囲に収まる、関係の「強さ」を示す純粋な指標とすることができます。
疑似相関と偏相関係数:「見せかけの関係」に騙されない
「相関関係は、因果関係を意味しない」
これは統計学で最も重要な格言の一つです。2つの変数に相関があっても、それが直接的な原因と結果の関係にあるとは限りません。というのも、2つの変数の相関は、その背後にある「第3の変数」によってもたらされた「疑似相関」である可能性もあるためです。
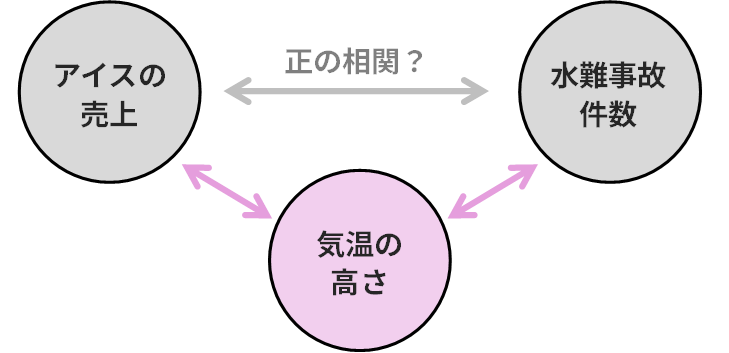
- 疑似相関 (Spurious Correlation):例えば、「アイスの売上」と「水難事故の件数」には強い正の相関があります。しかし、アイスが事故を引き起こしているわけではありません。「気温の高さ」という第3の変数が、両方を引き起こしていると考えられます。これが疑似相関です。
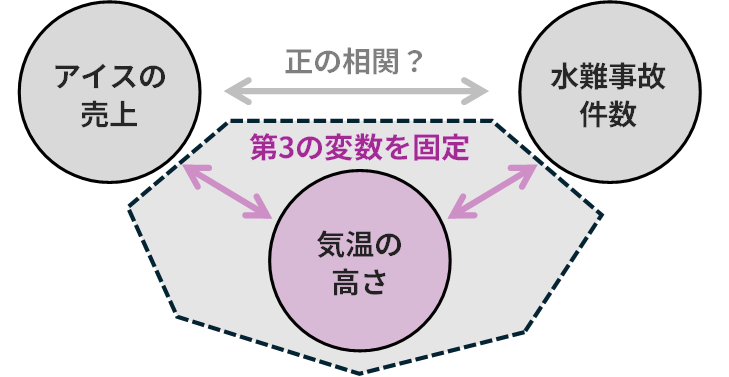
- 偏相関係数 (Partial Correlation Coefficient):この疑似相関を取り除くための道具が偏相関係数です。これは、第3の変数の影響を取り除いた後で、本来の2変数間の相関を計算するものです。上の例で言えば、「気温」の影響を固定した上で、それでも「アイスの売上」と「水難事故」に関係があるかを調べることができます。
偏相関係数の定義式
それでは、偏相関係数はどのようにして「第3の変数の影響」を取り除いているのでしょうか。その仕組みにおける考え方を確認し、その後に具体的な定義式を確認していきましょう。
偏相関係数の計算の考え方は、一言でいうと「残り物同士の相関を見ている」というイメージです。
- まず、変数 \(X\) の中から、変数 \(Z\) で説明できてしまう部分( \(Z\) の影響)を取り除きます。それによって「 \(Z\) では説明できない \(X\) の残り物」を準備します。
- 同様に、変数 \(Y\) の中から、変数 \(Z\) で説明できてしまう部分を取り除きます。それによって、「 \(Z\) では説明できない \(Y\) の残り物」を準備します。
- 上記の「残り物」同士がどれだけ相関しているかを計算します。

これにより、 \(Z\) という共通の原因の影響が排除され、 \(X\) と \(Y\) の間の純粋な関係性だけを評価することができるようになります。
偏相関係数の定義式
上記の考え方にもとづいて導かれる偏相関係数の定義式は、結果的に以下のかたちとなります。変数 \(X\) と \(Y\) の関係から変数 \(Z\) の影響を取り除いた偏相関係数( \(\rho_{XY \cdot Z} \) と書きます)が、それぞれの相関係数を使って以下のように計算できます。
\[
\rho_{XY \cdot Z} = \frac{\rho_{XY} – \rho_{XZ} \rho_{YZ}}
{\sqrt{(1 – \rho_{XZ}^{2})(1 – \rho_{YZ}^{2})}}
\]
- 分子:元々の相関( \(\rho_{XY}\) )から、 \(Z\) を経由する間接的な相関( \(\rho_{XZ} \, \rho_{YZ}\) )を引き算しています。まさに「残り物同士の相関」を表す部分です。
- 分母:計算結果が \(-1\) から \(+1\) の範囲に収まるように調整している「正規化」の部分です。
計算例:アイスと水難事故の偏相関
先ほどの例を用いて、具体的な数値で考えてみましょう。
- \(X\):アイスの売上
- \(Y\):水難事故の件数
- \(Z\):気温
各変数間の相関係数が、以下のように計算されたとします。
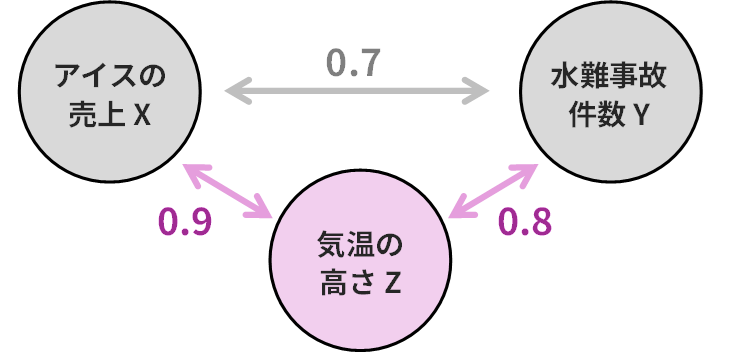
- アイス( \(X\) )と水難事故( \(Y\) )の相関 ( \(\rho_{XY} =0.7\) ) (強い正の相関)
- アイス( \(X\) )と気温( \(Z\) )の相関 ( \(\rho_{XZ} = 0.9\) ) (非常に強い正の相関)
- 水難事故( \(Y\) )と気温( \(Z\) )の相関 ( \(\rho_{YZ} = 0.8\) ) (強い正の相関)
このとき、「気温( \(Z\) )」の影響を取り除いた、アイス( \(X\) )と水難事故( \(Y\) )の偏相関係数 ( \(\rho_{XY \cdot Z}\) ) は以下のように計算できます。
\[\begin{align*}
\rho_{XY \cdot Z} &= \frac{0.7 – (0.9 \times 0.8)}{\sqrt{(1 – 0.9^2)(1 – 0.8^2)}} \\[6pt]
&= \frac{0.7 – 0.72}{\sqrt{(1 – 0.81)(1 – 0.64)\rule{0pt}{0.8em}}} \\[6pt]
&= \frac{-0.02}{\sqrt{0.19 \times 0.36 \rule{0pt}{1em}}} = \frac{-0.02}{\sqrt{0.0684 \rule{0pt}{1em}}} \\[6pt]
&= \frac{-0.02}{0.2616} \approx -0.076
\end{align*}\]
計算の結果、偏相関係数は \(-0.076\) となり、ほぼ \(0\) に近い値になりました。これは、元々 \(0.7\) もあった強い正の相関が、「気温」という共通の原因を取り除いた結果、ほとんど消えてしまったことを意味します。つまり、アイスの売上と水難事故の間の相関は、見せかけの相関(疑似相関)であった可能性が極めて高い、と結論づけることができます。
03. 期待値・分散の法則
期待値や分散の計算は、定義通りに行うと非常に面倒です。しかし、これから紹介する「法則」を使えば、複雑な計算をかなり簡略化することができます。
線形結合の期待値と分散
\(X\) と \(Y\) を確率変数、 \(a,b,c\) を定数とするとき、 \(Z=aX+bY+c\) のような新しい確率変数(これを「線形結合」と呼びます)の期待値 \(E[Z]\) と分散 \(V[Z]\) は、以下の公式で求められます。2級の対策で学習された方も多いかと思います。
\[\begin{align*}
E[Z]&=aE[X]+bE[Y]+c\\[5pt]
V[Z]&=a^{2} V[X] + b^{2} V[Y] + 2ab \, \mathrm{Cov}(X,Y)
\end{align*}\]
期待値はシンプルで、各々の期待値の定数倍を足し合わせたものとなります。分散は、各々の分散を定数倍ではなく、[定数の2乗]倍することに注意しましょう。また、最後に \(2ab \, \mathrm{Cov}(X,Y) \) が付くこともポイントです。これは、 \(X\) と \(Y\) が互いに関係しながら動くことによる分散の「相乗効果」を考慮するための項です。 \(X\) と \(Y\) の関係性によって以下のように整理されます。
- \(X\) と \(Y\) が独立: \(\mathrm{Cov}(X,Y)=0\) となり、この項は消えます。
- \(X\) と \(Y\) が正の相関: \(\mathrm{Cov}(X,Y)>0\) となり、 \(Z\) の分散を「促進」する効果があります。
- \(X\) と \(Y\) が負の相関: \(\mathrm{Cov}(X,Y)<0\) となり、 \(Z\) の分散を「抑制」する効果があります。
繰り返し期待値の法則
繰り返し期待値の法則とは「 \(Y\) の全体平均は、 \(X\) という条件ごとに見た平均を、さらに平均したものに等しい」というルールです。以下の数式で表現されます。
\[
E[Y]=E \bigl[ E \, [\,Y \mid X\,] \bigr]
\]
例えば「大学全体の学生の平均身長」を知りたいときに、以下のように2段階で考えていくイメージになります。
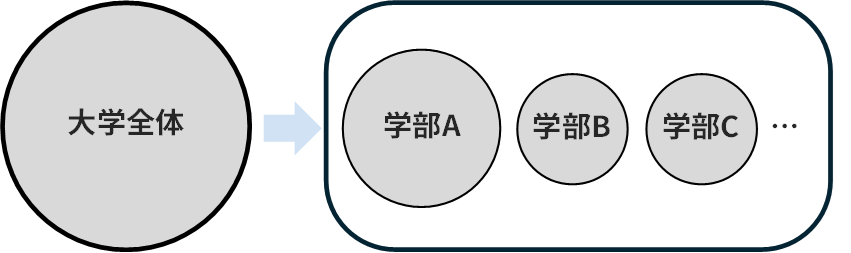
- 学部ごとに「その学部の平均身長」を出す
- 「学部ごとの平均身長」を学生数で重みづけしてもう一度平均する
繰り返し期待値の法則は頭が混乱しがちです。具体例を用いて実際に計算してみたいと思います。
<例題>ある大学では、学生アルバイトの時給 \(Y\) は 学部 \(X\) によって次のように違います。なお、この大学の学部は文学部と理学部のみであるものとします。

- 文学部の学生は平均時給 1,000円で、全体の 40%
- 理学部の学生は平均時給 1,200円で、全体の 60%
このとき、大学全体の学生アルバイトの平均時給(期待値) \(E[Y]\) は \(1000 \times 0.4 +1200 \times 0.6 =1120\) となります。これを繰り返し期待値の法則の視点で考えてみましょう。まずは学部ごとに「その学部の平均時給」は以下のように与えられています。
\[\begin{align*}
E \, [\,Y \mid X=\text{文学部}] &=1000\\[5pt]
E \, [\,Y \mid X=\text{理学部}] &=1200
\end{align*}\]
この「学部ごとの平均時給」を学生数の割合で重みづけしてもう一度期待値(平均)をとると、求めたい大学全体の平均時給(期待値)を以下のように導けます。
\[\begin{align*}
E[Y]&=E \bigl[ E \, [\,Y \mid X\,] \bigr]\\[5pt]
&=E \, [\,Y \mid X=\text{文学部}\,] \times E(X=\text{文学部}) \\[3pt]
& \;\; + E \, [\,Y \mid X=\text{理学部}\,] \times E(X=\text{理学部})\\[5pt]
&=1000 \times 0.4 + 1200 \times 0.6\\[5pt]
&=1120
\end{align*}\]
要するに、繰り返し期待値の法則は新しい計算方法というよりも、全体の期待値を「条件付きの期待値」に分解して眺め直したものと言えます。ただ、この「条件付き」の視点をもつことで計算が簡単になったり、意味づけがはっきりしたりすることがあり、非常に重要な法則となっています。
分散の条件付き分散による表現
分散についても「条件付き」の視点から整理することができます。
\[
V[Y]=E \bigl[ V \, [\,Y \mid X\,] \bigr] + V \bigl[ E \, [\,Y \mid X\,] \bigr]
\]
これは「全体のばらつき」は、「グループ内のばらつきの平均(期待値)」と「グループ別の平均のばらつき」の2つの要素に分解できる、という意味です。先ほどの平均時給の例題で言えば、「大学全体の時給のばらつき」=「(各学部の時給のばらつき)の平均」+「(各学部の平均時給)のばらつき」となります。
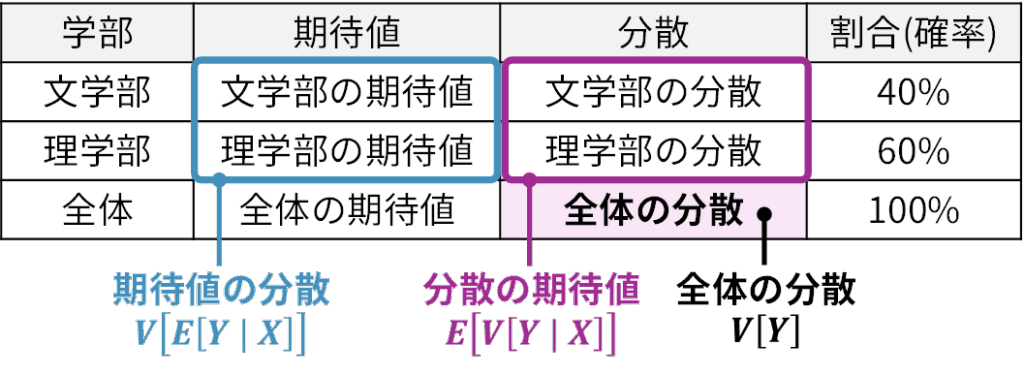
もう1つ別の例で考えてみましょう。ある会社ににおいて「営業部」と「開発部」の2つの部署があるとします。営業部の給与の分散は小さく、開発部の給与の分散も同様に小さいものとします。つまり「部内(グループ内)のばらつき」は小さいわけです。

ところが、営業部の平均給与(期待値)と開発部の平均給与(期待値)を比べると差が大きいとします。この場合、会社全体で給与の分散を計算すると、部内の分散だけでは説明できず、部ごとの平均の差(グループ間のばらつき) が効いてきます。その結果として、以下のように整理されます。
\[\begin{align*}
V[\text{全体の給与}]&=E \bigl[ V \, [\,\text{給与} \mid \text{部署}\,] \bigr]\\[4pt]
&\;\;+V \bigl[ E \, [\,\text{給与} \mid \text{部署}\,] \bigr]
\end{align*}\]
- 第1項 \(E \bigl[ V \, [\,\text{給与} \mid \text{部署}\,] \bigr]\) :部署ごとの給与のばらつきの平均
- 第2項 \(V \bigl[ E \, [\,\text{給与} \mid \text{部署}\,] \bigr]\) :部署ごとの平均給与のばらつき
つまり、「ばらつきの平均」と「平均のばらつき」が合わさって「全体のばらつき」になる、ということです。この考え方は分散分析(ANOVA)にもつながります。分散分析では、全体のばらつきを「グループ内のばらつき(上記の例では部署内の分散の期待値)」と「グループ間のばらつき(上記の例では部署間の期待値の分散)」に分けて、それぞれの大きさを比べることで、グループ間に有意な差があるかどうかを検定します。このように、条件付き分散の視点を用いた統計学的手法は少なくありませんので、これも重要な期待値・分散の性質の1つと言えます。
04. 多変量への拡張
これまでは1つか2つの確率変数を扱ってきましたが、実社会のデータはもっと多次元です。例えば、顧客データには「年齢」「性別」「購入金額」「来店頻度」など、多数の変数が含まれています。これらのデータをまとめて効率的に扱うための数学的な道具がベクトルと行列です。
ベクトルと行列
まずは、ベクトルと行列がどのようなものか、そのイメージを掴みましょう
ベクトル
「数字を順番に並べたもの」がベクトルです。例えば、ある顧客データにおいて、年齢の情報が次のように整理されていたとします。
- 1人目:30歳
- 2人目:25歳
- 3人目:40歳
これを横に並べると、 \((30, \, 25, \, 40)\) となります。これが行ベクトルです。各顧客の年齢データを1行にまとめたものと考えるとよいでしょう。なお、縦に並べた場合は列ベクトルと言い、行ベクトルを列ベクトルに(あるいは列ベクトルを行ベクトルに)変換することを「転置」と言います。ベクトルの右肩に「 \(\top\) 」という記号を付すことで「転置」を意味します。以下の式では、左辺が「行ベクトルの転置」を意味し、右辺が「列ベクトル」を意味しています。つまり、行ベクトルを転置すると列ベクトルとなり、また、列ベクトルを転置すると行ベクトルになります。
\[
(30,\;25,\;40)^\top
=\begin{pmatrix}
30 \\ 25 \\ 40
\end{pmatrix}
\]
行列
複数の行ベクトルを縦に並べたものが行列です。例えば、3人分の顧客データをまとめると、「顧客リスト」として以下のような表に整理できます。ここでは「年齢」のほかに「年収」と「満足度」というデータがあるものとします。
\[\begin{array}{c|ccc}
& \text{1人目} & \text{2人目} & \text{3人目} \\
\hline
年齢\; & 30 & 25 & 40 \\
年収\; & 400 & 550 & 300 \\
満足度\; & 4 & 3 & 5 \\
\end{array}\]
この顧客リストを数学的に行列表記すると以下のようになります。例えば、2行目の3列目の値(=300)は「年収」の「3人目」の情報を表しています。
\[\begin{pmatrix}
30 & 25 & 40 \\
400 & 550 & 300 \\
4 & 3 & 5
\end{pmatrix}\]
確率ベクトル
上記では手元にデータがある前提でベクトルや行列を考えてきました。ここで、それぞれの変数(年齢、年収、満足度)について、手元にまだデータはない「確率変数」として考えてみることにします。いま、年齢を確率変数 \(X_{1}\) 、年収を確率変数 \(X_{2}\) 、満足度を確率変数 \(X_{3}\) とすると、これらをまとめて以下のように表記できます。
\[\mathbf{X} =
\begin{pmatrix}
X_1 \\
X_2 \\
X_3
\end{pmatrix}\]
このように、複数の確率変数をひとつに束ねたものを確率ベクトルと呼びます。確率ベクトルを定義しておくと、個々の確率変数をバラバラに扱うのではなく、ベクトルや行列という統一的な枠組みで整理できるようになります。
期待値ベクトル
確率ベクトルを導入すると、各確率変数の平均的な値(期待値)をまとめて表現することが可能になります。具体的には、確率変数 \(X_1,X_2,X_3\) の期待値を並べて以下のように表記できます。
\[
\mathbf{\mu} = \begin{pmatrix} E[X_1] \\ E[X_2] \\ E[X_3] \end{pmatrix}
\]
上記の \(\mathbf{\mu}\) を期待値ベクトルと呼びます。これにより、「年齢の期待値」「年収の期待値」「満足度の期待値」をひとつのまとまりとして同時に扱えるようになります。さらに、これらの期待値を \(\mu_1=E[X_1]\) , \(\mu_2=E[X_2]\) , \(\mu_3=E[X_3]\) とおくと、期待値ベクトルは以下のように簡潔に表記できます。
\[
\mathbf{\mu} = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{pmatrix}
\]
分散共分散行列
さらに重要なのが、確率変数同士のばらつきや関係性を表す分散共分散行列です。これは各確率変数の分散だけでなく、異なる確率変数同士の共分散を行列の形で整理したものです。確率ベクトル \(\mathbf{X} = (X_1, X_2, X_3)^{\top}\) に対する分散共分散行列は以下のように整理されます。
\[
\Sigma =
\begin{pmatrix}
\mathrm{Cov}(X_1,X_1) & \mathrm{Cov}(X_1, X_2) & \mathrm{Cov}(X_1, X_3) \\
\mathrm{Cov}(X_2, X_1) & \mathrm{Cov}(X_2, X_2) & \mathrm{Cov}(X_2, X_3) \\
\mathrm{Cov}(X_3, X_1) & \mathrm{Cov}(X_3, X_2) & \mathrm{Cov}(X_3, X_3)
\end{pmatrix}
\]
この行列 \(\Sigma\) は、「総当たりの一覧表」 のようなものです。行と列に変数の名前を書いて、その交わるマス目に「その2つの変数の関係(分散や共分散)」を入れていくイメージです。たとえば、「年齢 \(X_{1}\) 」という行と、「年収 \(X_{2}\) 」という列の交点(1行2列目)には「年齢と年収の共分散:\(\mathrm{Cov}(X_1,X_2)\) 」が入ります。

ここで、同一の確率変数についての共分散はすなわちその確率変数の分散となります。例えば、 \(\mathrm{Cov}(X_1,X_1)=V[X_1]\) です。したがって、上記の分散共分散行列の対角線上の共分散を分散で書き換えると以下のように表記することができます。
\[
\Sigma =
\begin{pmatrix}
V[X_1] & \mathrm{Cov}(X_1, X_2) & \mathrm{Cov}(X_1, X_3) \\
\mathrm{Cov}(X_2, X_1) & V[X_2] & \mathrm{Cov}(X_2, X_3) \\
\mathrm{Cov}(X_3, X_1) & \mathrm{Cov}(X_3, X_2) & V[X_3]
\end{pmatrix}
\]
上記の分散共分散行列の表記はやや冗長です。そこで、記号を簡略化するために、それぞれの分散・共分散を \(\sigma\) と添え字 \(i\) , \(j\) を用いて以下のように表記することにします。
\[
\sigma_{ij}=\mathrm{Cov}(X_i, X_j)
\]
ここでは、\(i\) が行番号、 \(j\) が列番号を意味しています。そして、第 \(i\) 行目の確率ベクトル \(X_{i}\) と、第 \(j\) 列目の確率ベクトル \(X_{j}\) の共分散を「 \(\sigma_{ij}\) 」と表記しています。例えば、\(\sigma_{23}\) と書けば、第 \(2\) 行目の確率ベクトル \(X_{2}\) と、第 \(3\) 列目の確率ベクトル \(X_{3}\) の共分散、ということになります。また、\(\sigma_{22}\) と書けば、第 \(2\) 行目の確率ベクトル \(X_{2}\) と、第 \(2\) 列目の確率ベクトル \(X_{2}\) の共分散、すなわち、これは確率ベクトル \(X_{2}\) の分散ということになります。この表記を用いると、先ほどの分散共分散行列を以下のように整理できます。
\[
\Sigma =
\begin{pmatrix}
\sigma_{11} & \sigma_{12} & \sigma_{13} \\
\sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{pmatrix}
\]
このように \(\sigma_{ij}\) という記号を導入することで、行列の形がより見やすく整理されました。ここで、行列の中のひとつひとつの要素を成分と呼びます。成分の中でも、左上から右下にかけての対角に並んだ部分( \(\sigma_{11}, \sigma_{22}, \sigma_{33}\) )を対角成分といいます。分散共分散行列の対角成分は、それぞれの確率ベクトルの分散 \(V[X_i]\) に対応します。一方で、それ以外の位置にある要素(例えば \(\sigma_{12}, \sigma_{23}\) など)は非対角成分と呼ばれ、これは各確率ベクトル組の共分散 \(\mathrm{Cov}(X_i, X_j)\) に対応することになります。つまり分散共分散行列は、対角成分に分散をとり、非対角成分に共分散をとる行列ということになります。
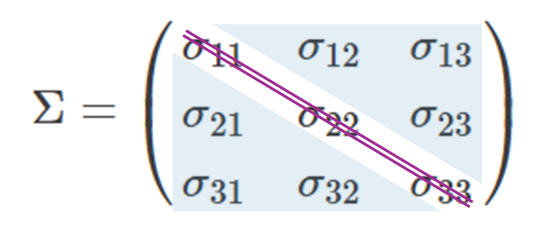
さらに重要なのは、この分散共分散行列は対称であるという点です。「対称」とは、行列を主対角線(左上から右下に向かって斜めに並んでいる成分を結んだ線)で折り返したときに、重なり合う成分が一致することを意味します。上記の分散共分散行列においては、\(\sigma_{12} = \sigma_{21}\) , \(\ \sigma_{13} = \sigma_{31}\) , \(\sigma_{23} = \sigma_{32}\) が成り立ちます。これは「 \(\mathrm{Cov}(X_i, X_j)\) と \(\mathrm{Cov}(X_j, X_i)\) は同じ値になる」という性質を反映しています。
また、分散共分散行列は非負定値行列である点もポイントです。ただ、非負定値行列についての説明にはやや応用的な線形代数の理解も必要となります。そこで以下では、この「分散共分散行列が非負定値行列である」ことについて、いまの段階で最低限おさえておくべき内容に絞って整理しました。細かい話はこの段階では読み飛ばしていただいても問題ありませんが、目を通しておくと後で役に立つことがあるかと思います。
【応用】分散共分散行列は「非負定値行列」(最低限の理解)
- 1次元の分散は必ず0以上
1つの変数の分散は「ばらつきの大きさ」なので、どんな場合も0以上です。 - 多次元では「非負定値」という形で表す
複数の変数をまとめた分散共分散行列 \(\Sigma\) は、その各要素(分散や共分散)の一部には負の値も含まれます。しかしここでいう「非負」とは要素1つ1つの符号のことではなく、行列全体を一つの仕組みとして見たときに0以上の性質が保たれるということです。この性質を「非負定値」と呼びます。 - 各成分を部品として組み合わせる=線形結合の分散
行列はただの数の並びなので、そのままでは「正」や「負」と言えません。そこで、任意の係数ベクトル \(\mathbf{x}\) を使って以下のように行列を挟みます。
\[\mathbf{x}^{\top} \Sigma \, \mathbf{x}\]
このようにベクトルで行列を挟むことで、行列を1つの数値に展開できます。具体的には、分散共分散行列 \(\Sigma\) の各成分を部品として組み合わせたような計算式となります(このような計算を二次形式と呼びます。詳細は後述の別記事で確認しましょう)。そしてこの計算の結果が「係数 \(\mathbf{x}\) で作った新たな確率変数(線形結合) \(Z= \mathbf{x}^{\top} \mathbf{X} \) の分散」を表し、統計の基本性質としてその分散は必ず
\[\mathbf{x}^{\top} \Sigma \, \mathbf{x} \ge 0 \]
となります。どんな係数ベクトルを選んでもこの不等式が成り立つということ。これこそが「分散共分散行列が非負定値である」という意味になります。
腕試し!模擬問題に挑戦
それではここまで学んだ知識を使って実力を試してみましょう!
模擬問題1
模擬問題1:問題
以下の問いについて、加重平均、幾何平均、調和平均の中から最も適切な平均を選び、その値を求めよ。
(1) あるファンドが3年間で、1年目は10%の利益、2年目は20%の損失、3年目は15%の利益を上げた。この3年間の年平均リターン(伸び率)を求めよ。
(2) ある青果店で、りんご(1個150円)が100個、みかん(1個50円)が300個、ぶどう(1房800円)が50房売れた。売れた果物1つあたりの平均価格を求めよ。
(3) ある工場にはAとBの2つの生産ラインがあり、それぞれ同じ量の製品を生産している。ラインAでは平均して200個に1個の割合で不良品が発生し、ラインBでは平均して50個に1個の割合で不良品が発生する。工場全体で、1個の不良品が発生するまでに生産される製品の数の平均を求めよ。
模擬問題1:解説
(1) 幾何平均が適切です。伸び率はそれぞれ1.1, 0.8, 1.15となります。
\[\begin{align*}
\text{平均伸び率}
&= \left(1.1 \times 0.8 \times 1.15\right)^{\tfrac{1}{3}}\\
&\approx (1.012)^{\tfrac{1}{3}}\approx 1.004
\end{align*}\]
年平均リターンは約0.4%の利益となります。
答え:\( \text{約} 1.004\)
(2) 加重平均が適切です。売り上げ個数が重みとなります。
\[\begin{align*}
\text{平均価格} &= \frac{150 \times 100 + 50 \times 300 + 800 \times 50}{100 + 300 + 50} \\[6pt]
&= \frac{15000 + 15000 + 40000}{450} \\[6pt]
&= \frac{70000}{450} \approx 155.6\ \text{円}
\end{align*}\]
答え:\(\text{約} 155.6 \text{円}\)
(3) 調和平均が適切です。調和平均は公式に値を代入してもよいのですが、割合と実数が混在して混乱しがちです。そこでここでは公式に頼らずに順を追って考えてみましょう(最後に公式と整合することも確認します)。
この問題は、異なる「発生率(割合)」を持つ複数のグループを統合した際の、全体の平均率を考える問題です。与えられた \(200\) , \(50\) という2つの数値から、単純に \( (200+50)/2=125\) 個と算術平均で計算するのは間違いです。これは、不良品の「見つかりやすさ」(発生率)が2つのラインで大きく異なるため、単純に個数を平均することはできないからです。
この問題の本質は、「製品1個あたりの平均不良品発生率」をまず求めることです。
- ラインAの発生率: \(\dfrac{1個}{200個} = \dfrac{1}{200}\)
- ラインBの発生率: \(\dfrac{1個}{50個} = \dfrac{1}{50}\)
両ラインの生産量は同じなので、工場全体の不良品の平均発生率は、これらの率の算術平均で計算できます。
\[\begin{align*}
\text{平均発生率} &= \dfrac{1}{2}\times\dfrac{1}{200} + \dfrac{1}{2}\times\dfrac{1}{50} \\[6pt]
&= \dfrac{1 + 4}{400} = \dfrac{5}{400} \\[6pt]
&= \dfrac{1}{80}
\end{align*}\]
この「 \(1/80\) 」という率は、「製品を \(1\) 個生産すると、平均して \(1/80\) 個の不良品が発生する」ことを意味します。 問題で問われているのは「 \(1\) 個の不良品が発生するのに必要な平均生産数」なので、この平均発生率の逆数を求めます。
\[\begin{align*}
\text{平均生産数} &= \frac{1}{\text{平均発生率}} \\[6pt]
&= \frac{1}{\tfrac{1}{80}} = 80\, \text{個}
\end{align*}\]
最後に、調和平均の計算式(逆数の平均の逆数)に値を代入する方法でも計算してみます。以下の通り、上記の計算過程と同様になることを確認しておきましょう。
\[\begin{align*}
\text{調和平均} &= \frac{n}{\displaystyle\sum_{i=1}^{n}\frac{1}{x_i}} \\[3pt]
&= \frac{2}{\frac{1}{200} + \frac{1}{50}} = \frac{2}{\frac{1 + 4}{200}} \\[6pt]
&= \frac{2 \times 200}{5} = 80
\end{align*}\]
答え:\(80 \, \text{個}\)
模擬問題2
模擬問題2:問題
あるカフェで、コーヒー1杯とマフィン2個をセットで販売している。コーヒー1杯の重さを \(X\,g\) 、マフィン2個の重さをそれぞれ \(Y_{i}\, g\; (i=1,2) \) とする。\(X,\,Y_{i}\) は互いに独立な確率変数で、それぞれの期待値と分散は以下の通りである。
\[\begin{align*}
E[X]&=150g, \; V[X]=10^{2}\\[6pt]
E[Y_{i}]&=80g, \; V[Y_{i}]=5^{2}
\end{align*}\]
コーヒーは重さ \(10g\) のカップで、マフィン2個は重さ \(5g\) の1枚の皿でお客様に提供される。このとき、お客様に提供されるセット全体(コーヒー、マフィン、カップ、皿)の重さの合計 \(W\) の期待値と分散を求めよ。
模擬問題2:解説
コーヒーの重量を提供されるセット全体の重さ \(W\) は
\[\begin{align*}
W&=(X+10)+(Y_{1}+Y_{2}+5)\\
&=X+Y_{1}+Y_{2}+15
\end{align*}\]
と表せます。したがって、期待値 \(E[W]\) は以下のように整理できます。
\[\begin{align*}
E[W]&=E[X+Y_{1}+Y_{2}+15]\\
&=E[X]+E[Y_{1}]+E[Y_{2}]+15\\
&=150+80+80+15=325g
\end{align*}\]
また、分散 \(V[W]\) は以下のように整理できます。\(X\) , \(Y_{i}\) は互いに独立なので、それぞれの組み合わせの共分散は0であること、また、定数を足しても分散は変化しないことに注意しましょう。
\[\begin{align*}
V[W]&=V[X+Y_{1}+Y_{2}+15]\\
&=V[X]+V[Y_{1}]+V[Y_{2}]\\
&=10^{2}+5^{2}+5^{2}=150
\end{align*}\]
答え:期待値 \(325g\) 、分散 \(150\)
模擬問題3
模擬問題3:問題
ある集団が受験した4教科(国語、数学、理科、社会)のテスト結果について、それぞれの点数を確率変数 \(X_1\) , \(X_2\) , \(X_3\) , \(X_4\) とし、これらの確率変数をまとめた確率ベクトルを以下の \(\mathbf{X}\) で表記することにします。
\[
\mathbf{X} =
\begin{pmatrix}
X_{1}\\
X_{2}\\
X_{3}\\
X_{4}
\end{pmatrix}
\]
また、この確率ベクトル \(\mathbf{X}\) についての期待値ベクトル \(\mathbf{\mu}\) と分散共分散行列 \(\Sigma\) が、以下のように与えられているとします。
\[ \mathbf{\mu}=\begin{pmatrix}
65\\
58\\
62\\
68
\end{pmatrix} \]
\[ \Sigma=\begin{pmatrix}
121 & 30 & 50 & 70 \\
30 & 225 & 80 & 25 \\
50 & 80 & 144 & 60 \\
70 & 25 & 60 & 100
\end{pmatrix}\]
(1) このテストの理科( \(X_3\) )の期待値を答えよ。
(2) このテストの数学( \(X_2\) )と社会( \(X_4\) )の共分散を答えよ。
模擬問題3:解説
以下の期待値ベクトル \(\mathbf{\mu}\) と分散共分散行列 \(\Sigma\) を読み取る問題です。
\[ \mathbf{\mu}=\begin{pmatrix}
65\\
58\\
62\\
68
\end{pmatrix} \]
\[ \Sigma=\begin{pmatrix}
121 & 30 & 50 & 70 \\
30 & 225 & 80 & 25 \\
50 & 80 & 144 & 60 \\
70 & 25 & 60 & 100
\end{pmatrix}\]
(1) 理科の点数 \(X_{3}\) は確率ベクトル \(\mathbf{X}\) の3番目の成分ですので、その期待値は、期待値ベクトルの3番目の成分となります。
答え \(62\) 点
(2) 数学の点数 \(X_{2}\) と社会の点数 \(X_{4}\) はそれぞれ確率ベクトル \(\mathbf{X}\) の2番目と4番目の成分ですので、その共分散は、分散共分散行列の2行目と4列目(または4行目と2列目)が交わる場所の成分となります。
答え \(25\)
まとめ
今回もお疲れさまでした!今回は、データの特徴を捉えるための様々な「特性値」を学びました。
- 平均:状況に応じて、算術・加重・幾何・調和を使い分ける。
- ばらつき:変動係数を使えば、異なるグループのばらつきを比較できる。
- 形:歪度・尖度で、分布の歪みや尖り具合がわかる。
- 関係性:相関係数で関係の強さを測り、偏相関係数で疑似相関を見抜く。
- 法則:期待値や分散の法則は、複雑な計算の強力な味方。
- 多次元:確率ベクトル、期待値ベクトル、分散共分散行列の読み方を知る。
特性値の話は基本的には2級の範囲の復習になりますが、繰り返し期待値の法則など「条件付き」の期待値や分散を用いた計算は慣れない部分が多いかと思います。この後も登場することがありますので、読み進めながら慣れていきましょう。また、確率ベクトルという考え方を通じて、線形代数の知識に足を踏み入れることができました。ベクトルや行列について、焦らずに、必要なタイミングで必要な知識を習得していくようにしましょう!次回は第4回「変数変換」です!


