こちらは統計学に関する暗記シートです。まずは記述統計に関する知識を1ページに整理しました。統計検定®2級対策など統計学の学習にぜひご活用ください。
統計学を学習されている方々に届くように
ぜひシェアをお願いします!
1. 記述統計
(1) 変数と尺度
変数は質的変数と量的変数に整理されます。また、量的変数は連続変数と離散変数に整理されます。
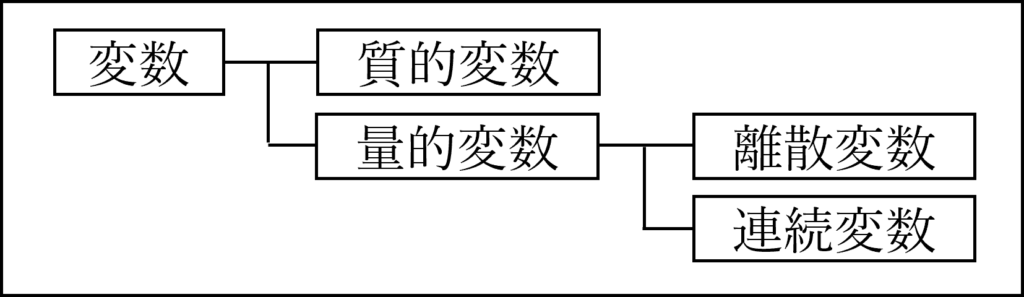
変数の尺度は4つの種類(名義尺度、順序尺度、間隔尺度、比例尺度)があります。

(2) 代表値と散布度
変数の「中心」をあらわす代表値として「平均」があり、「ばらつき」をあらわす散布度として「(標本)分散」「標準偏差」があります。
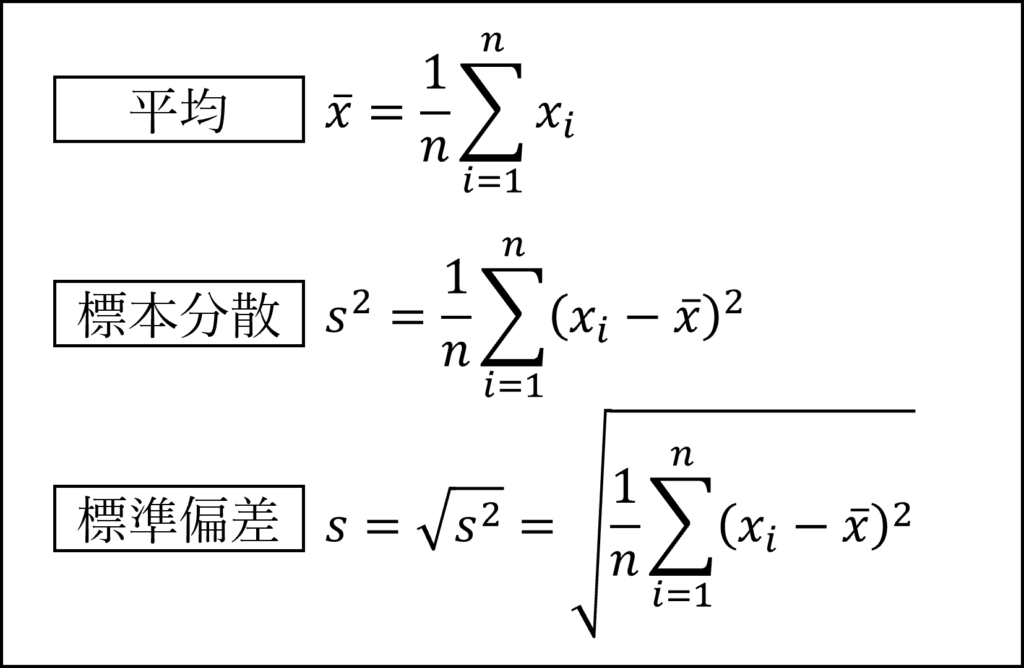
変数について平均を引いて標準偏差で割ることで標準化得点に変換できます。標準化得点は平均0、標準偏差1となります。
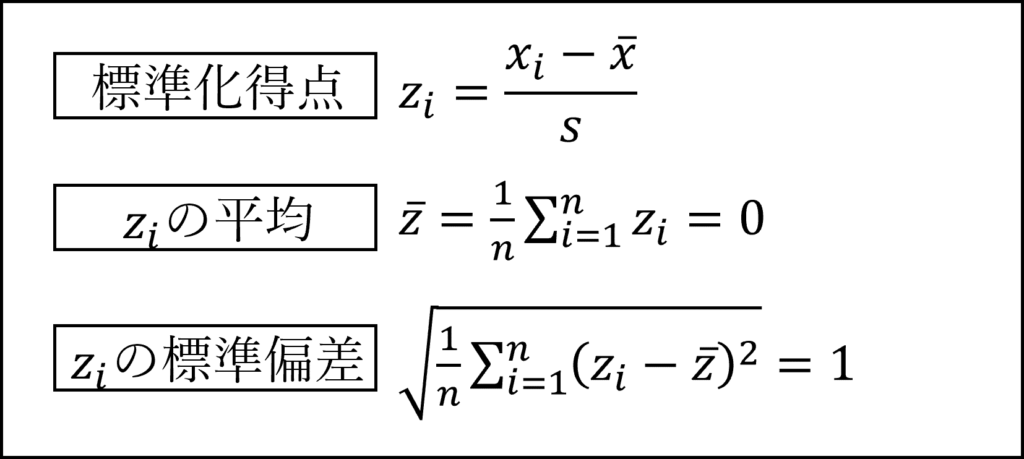
変動係数は、変数の変動(標準偏差)が平均の水準に比べてどの程度かをあらわします。
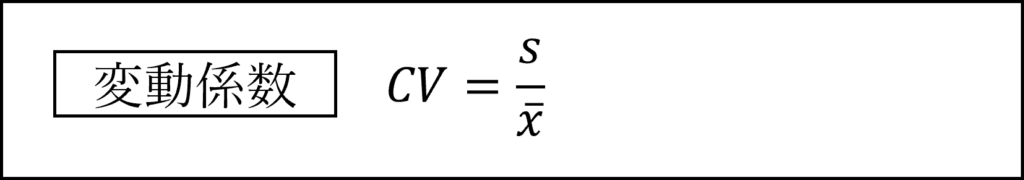
平均以外の代表値として「中央値」や「最頻値」などがあります。

(3) 分布と範囲
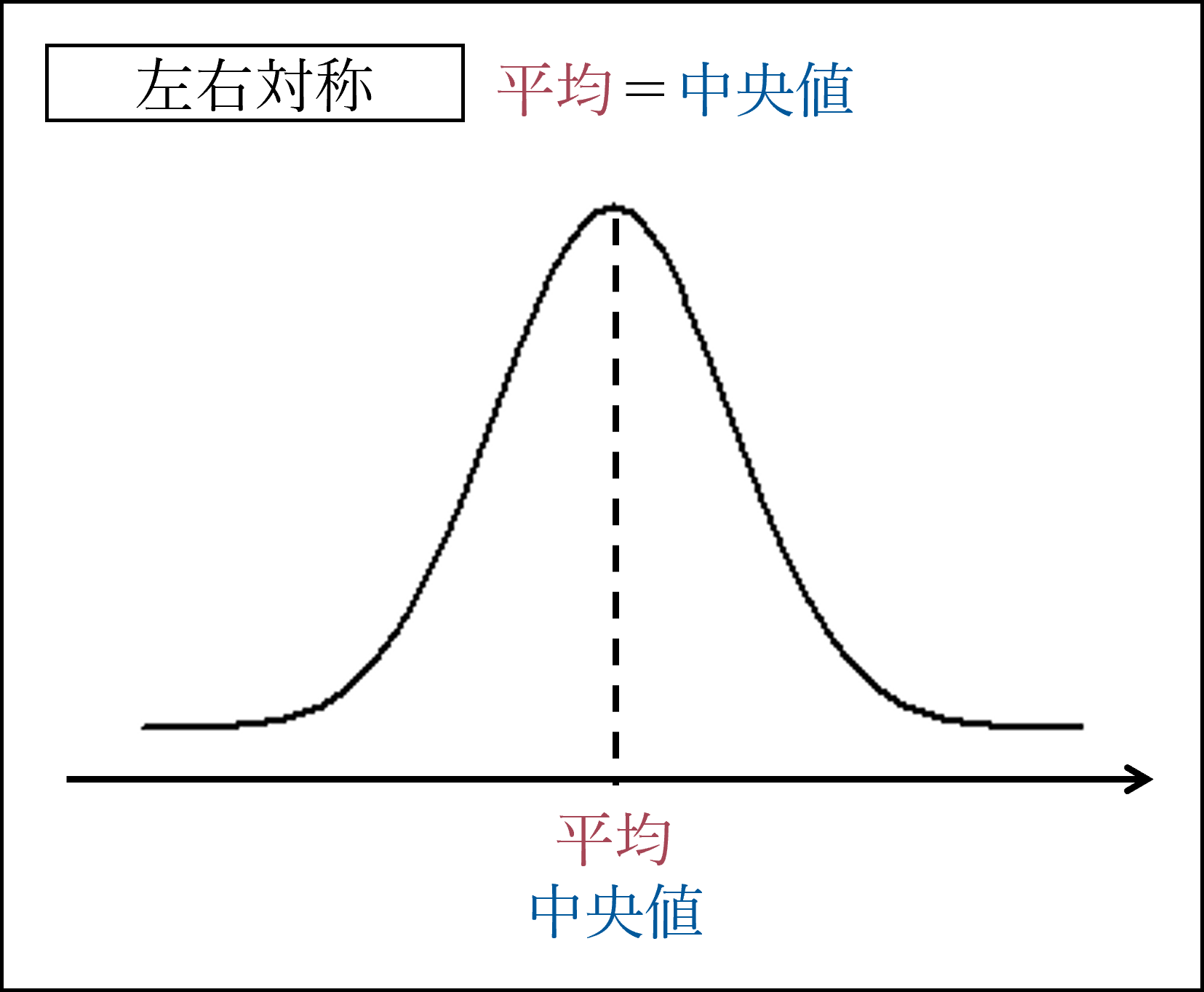
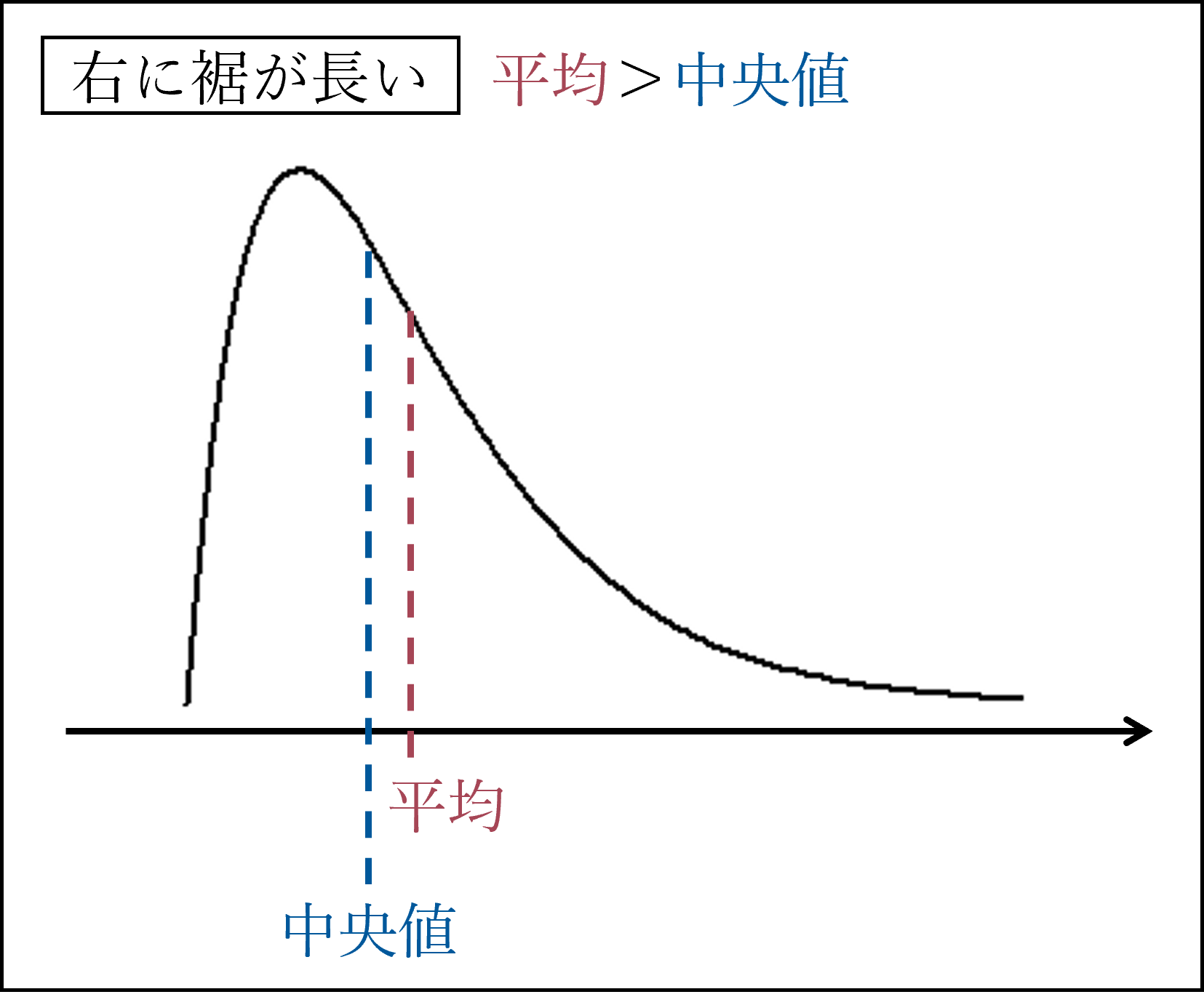
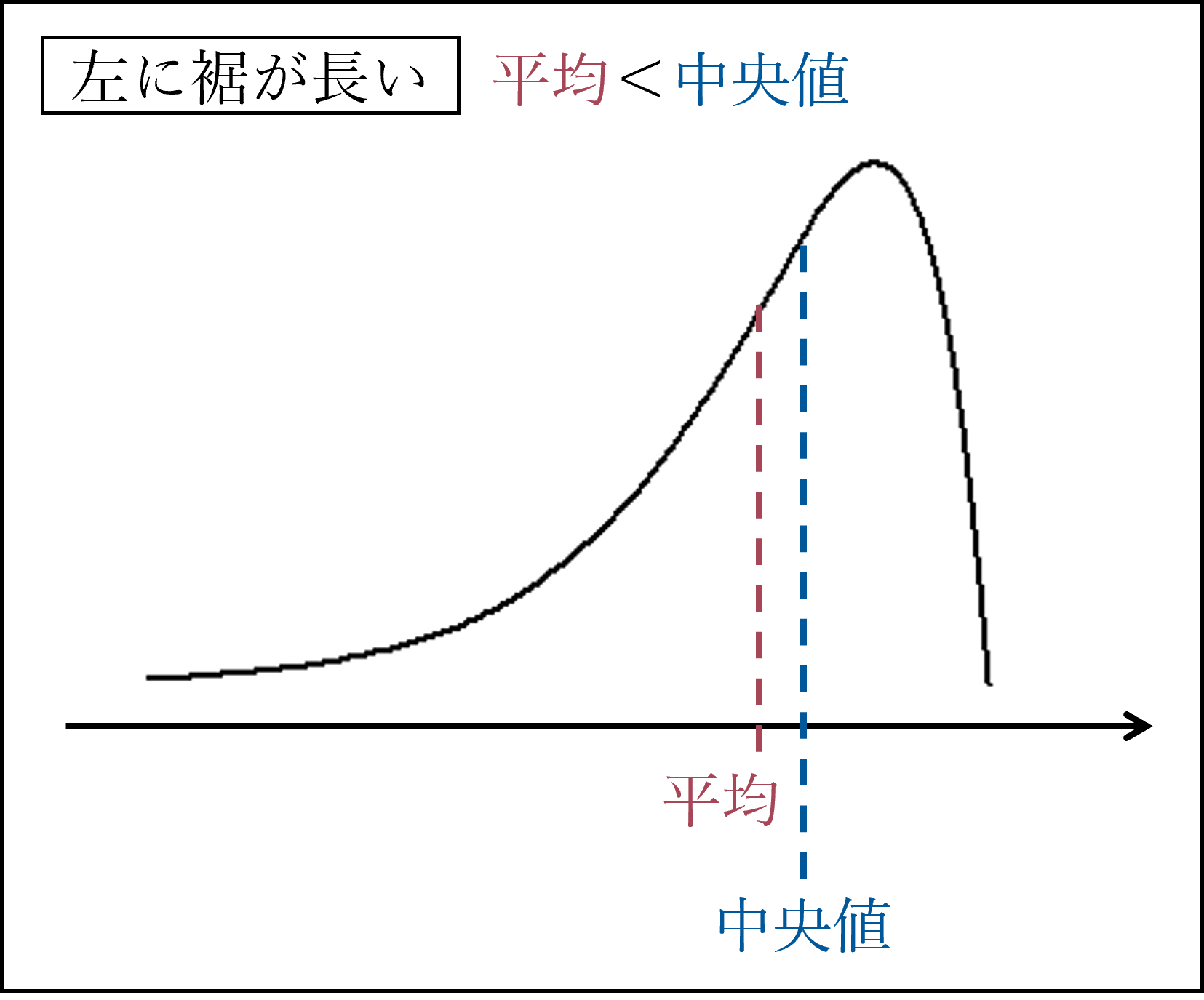
分布の形状(左右対称 / 右に裾が長い / 左に裾が長い)によって平均と中央値の不等号が変化します。
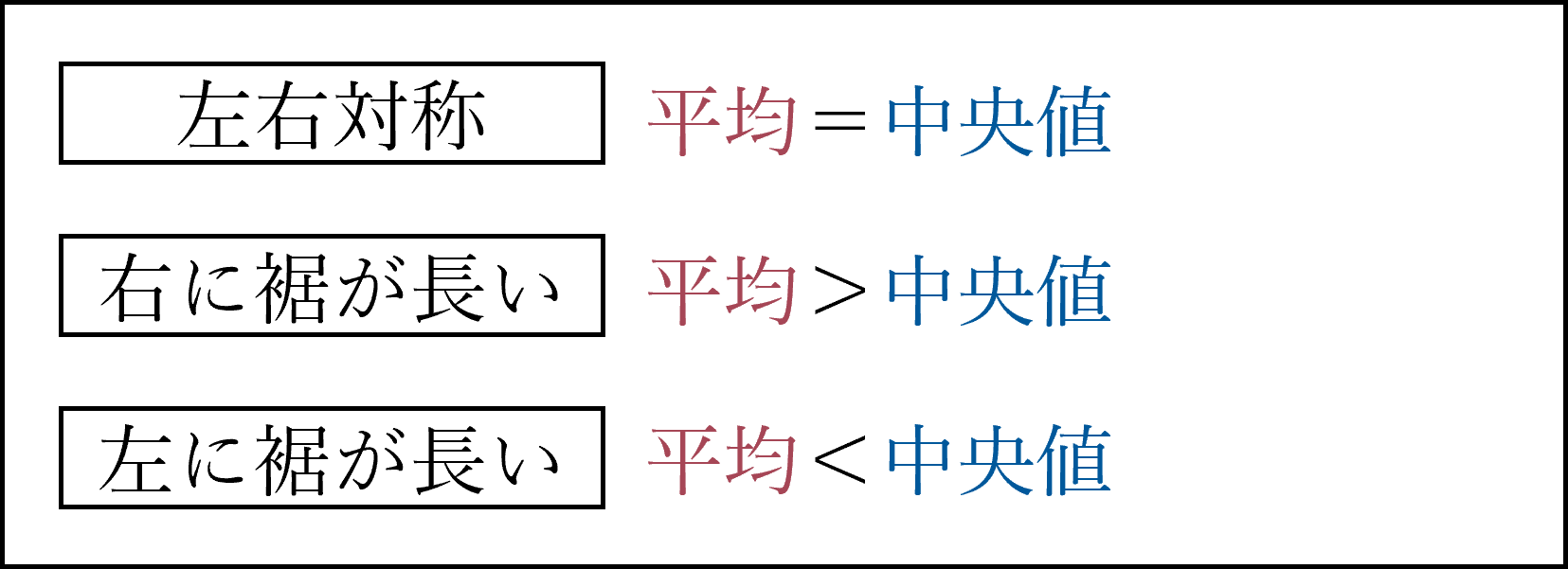
分布の形状を具体的に確認しておきましょう。
最大値と最小値の差を範囲と呼び、第3四分位数(75%点、Q3)と第1四分位数(25%点、Q1)の差を四分位範囲と呼びます。

箱ひげ図は「箱」と「ひげ」で観測値の分布を可視化する図です。「箱」と「ひげ」の長さは以下のようになります。

以下は箱ひげ図のサンプルです。ある学校の5教科の点数分布をイメージして作成した架空のデータを箱ひげ図にしています。
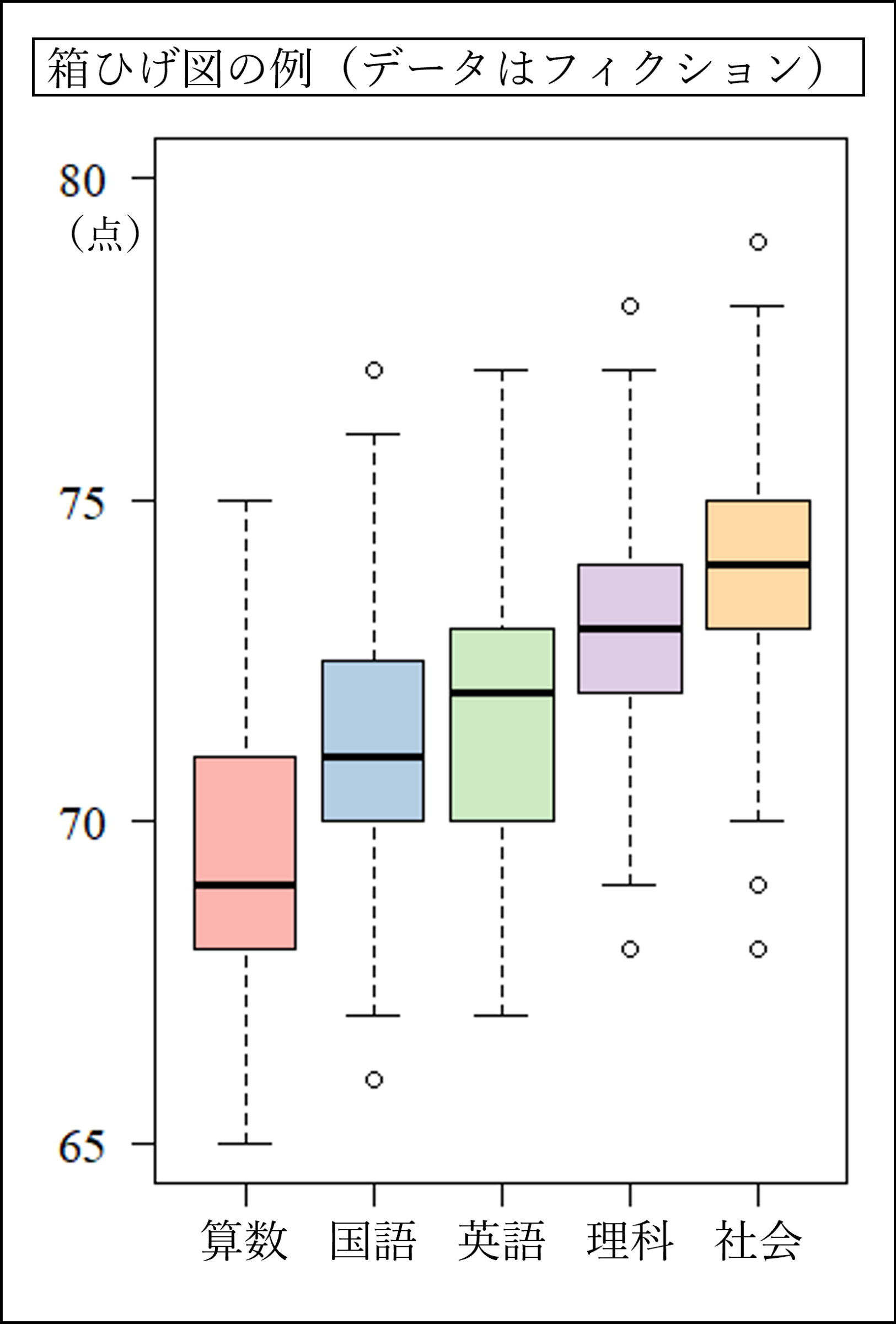
※各教科の中央値は算数69点、国語71点、英語72点、理科73点、社会74点で、箱の中の横線にて表示されます。
※ひげの外側にプロットされた点は外れ値です。外れ値は「ひげの長さの上限(1.5×箱の長さ)」を超えている観測値のことで、ひげの外側に〇印でプロットされます。
分布の形状を測る指標として歪度(わいど)と尖度(せんど)があります。
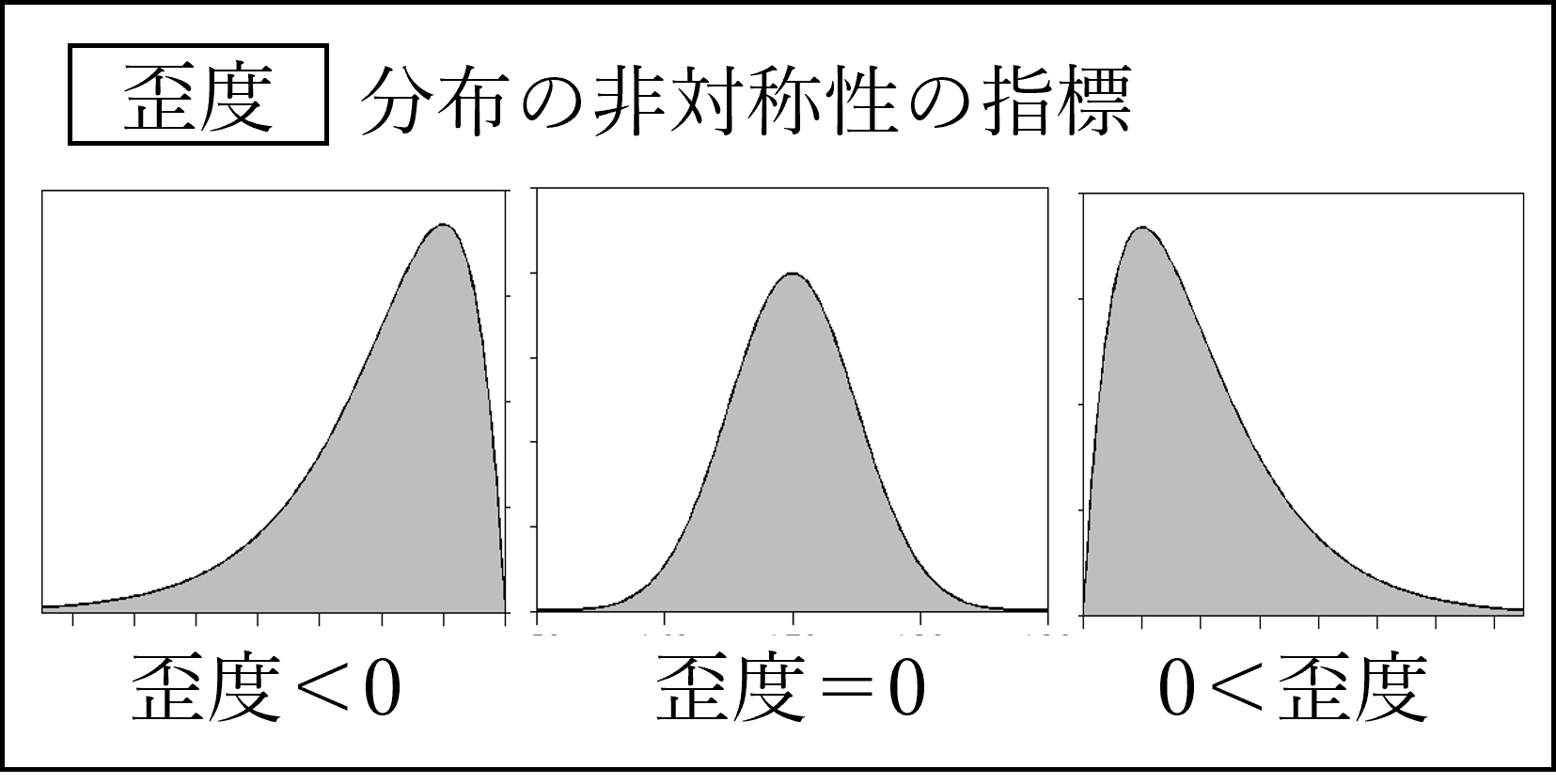
歪度は左右対称のとき0になり、右に裾が長いとき正の値、左に裾が長いとき負の値となります。「右・正・歪(うっ・せい・わい)」と覚えましょう。
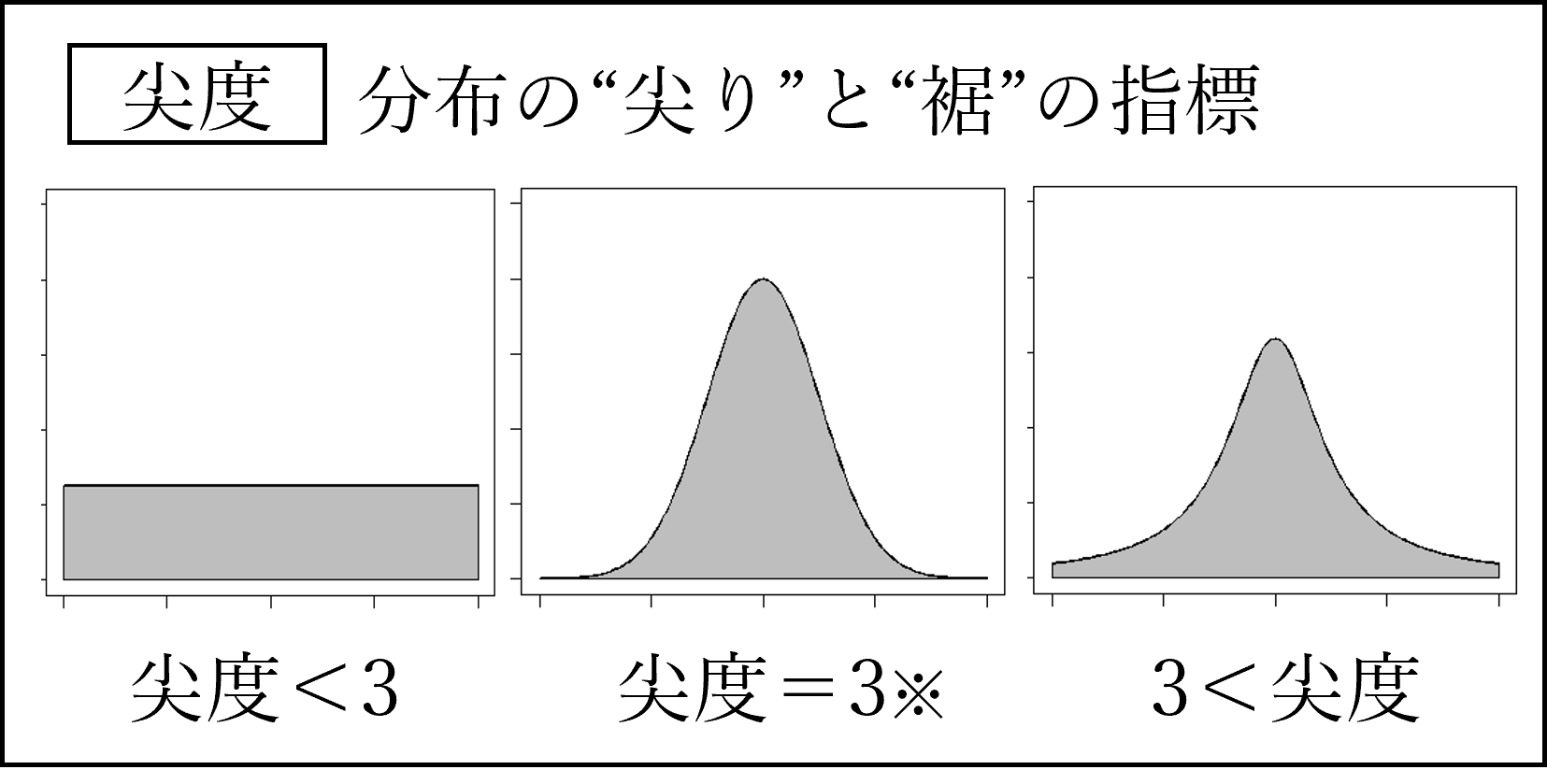
尖度は正規分布のとき3(※)となります(※正規分布のとき0となるように「-3」した値を尖度とする定義もあります)
(4) 共分散と相関
2変数の関係をあらわす指標として「共分散」と「相関係数」があります。
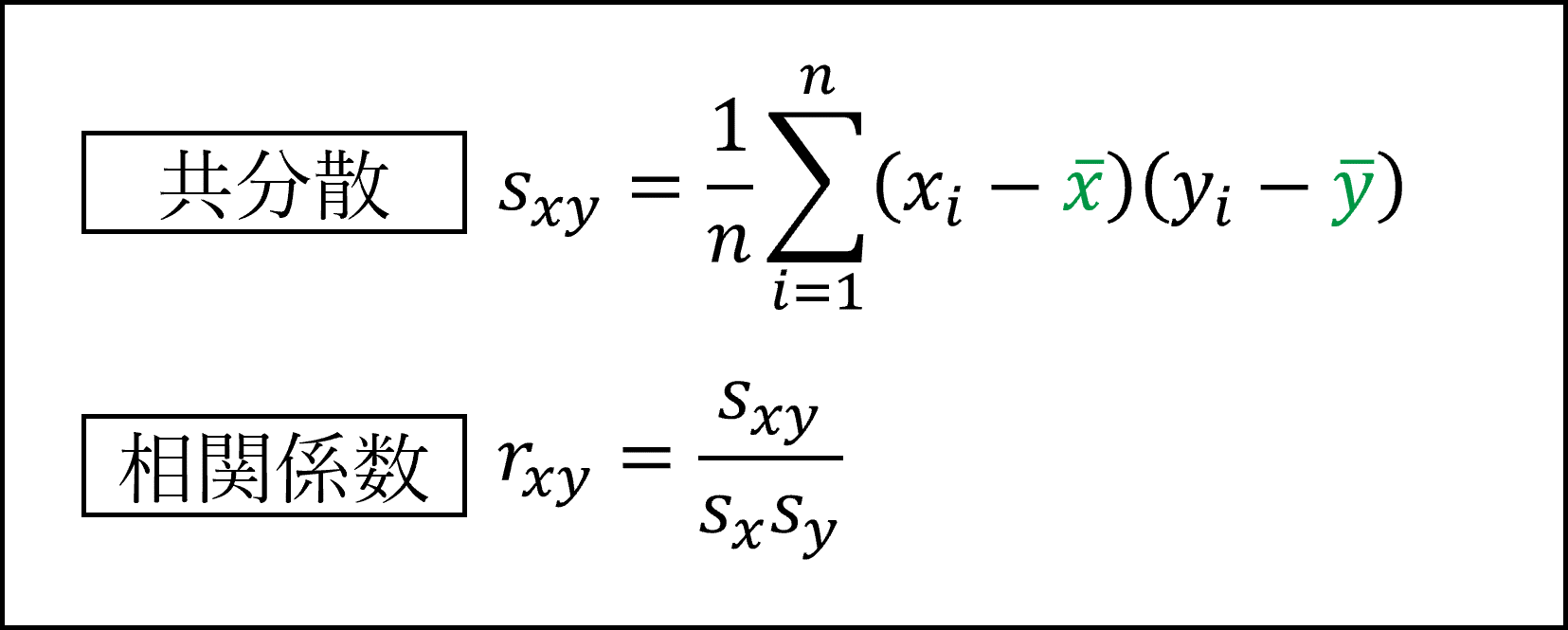
共分散は視覚的には各観測値が平均ライン(緑線)との間で作る四角形の面積(以下図の色塗り部分)を合計してnで割ったもの※として表現されます。右上と左下の領域の符号がプラス、左上と右下の領域の符号がマイナスになります。
※推測統計学の文脈では不偏性を考慮してnではなくn-1で割って計算されます。
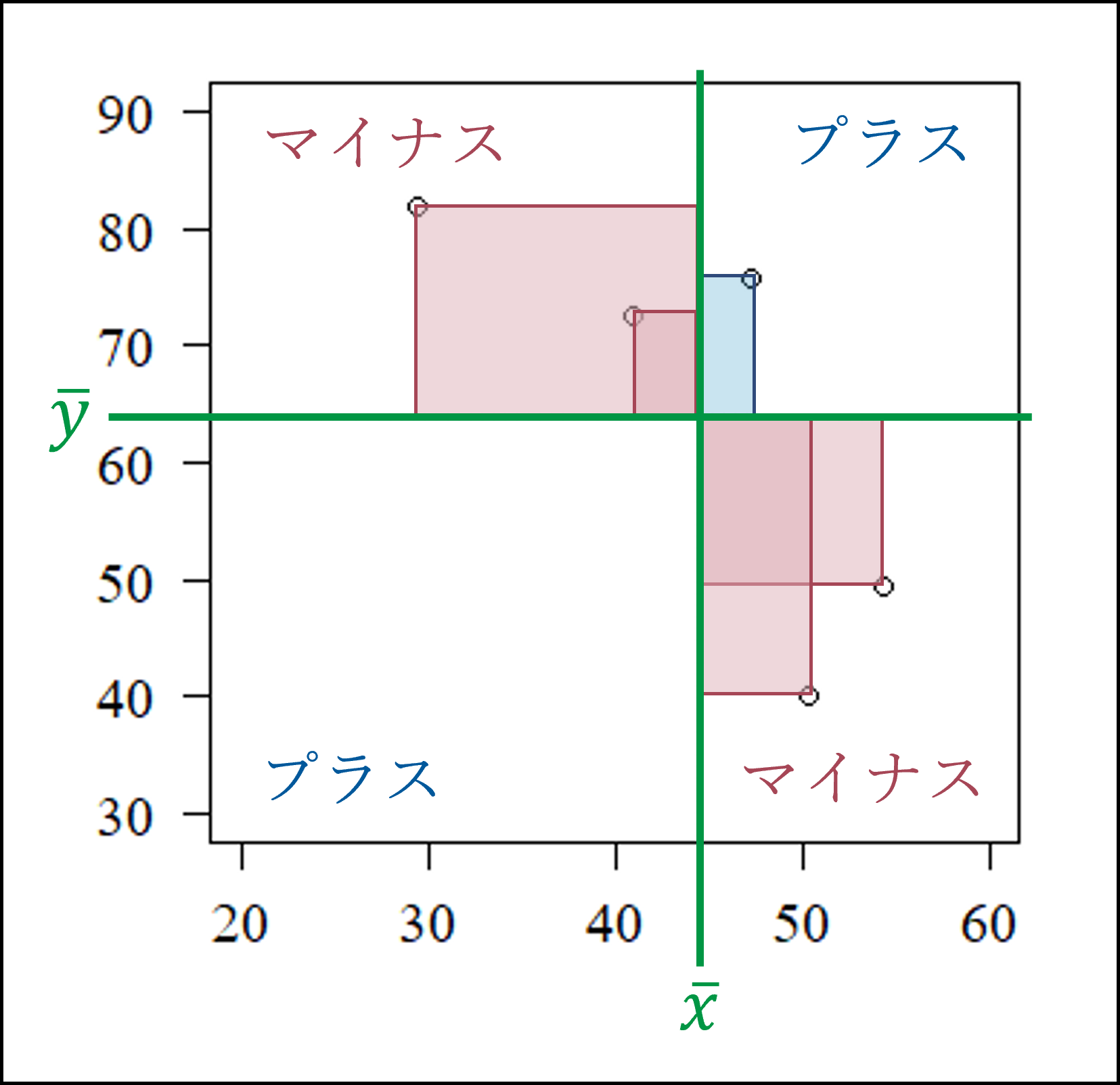
- 右上と左下の領域(右肩上がりの領域)に観測値が集まっていれば共分散および相関係数はプラス(正の相関)になります。
- 左上と右下の領域(右肩下がりの領域)に観測値が集まっていれば共分散および相関係数はマイナス(負の相関)になります。
- 左上・右上・右下・左下の領域に満遍なく観測値がバラついている場合は共分散および相関係数は0(無相関)に近くなります。
相関係数は2つの変数の標準化得点による式に変形できます。

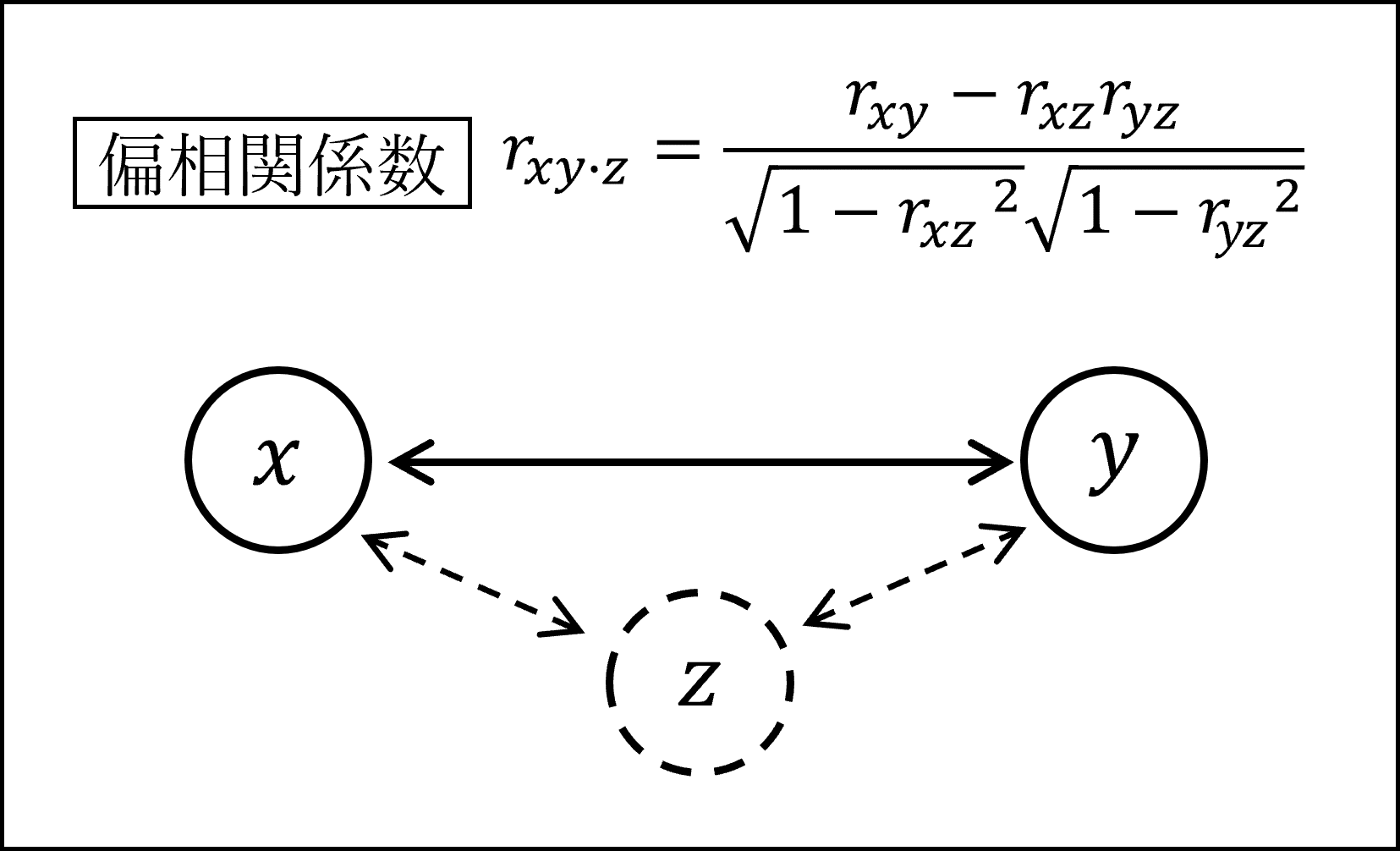
第3の変数の影響を除外した相関関係を確認したい場合は「偏相関係数」を用います。
(5) 回帰直線
回帰直線は目的変数を説明変数と回帰係数(定数項と傾き)によって表現される直線で、以下の式で定義されます。

※以下、定数項を含む回帰直線を前提としています。定数項を含まない回帰直線(y=βx)が出題されたこと(以下をご参照ください)もありますのでご注意ください。
推定された回帰直線は一般に「^(ハット)」を記号の上部に付して以下のように表記します。

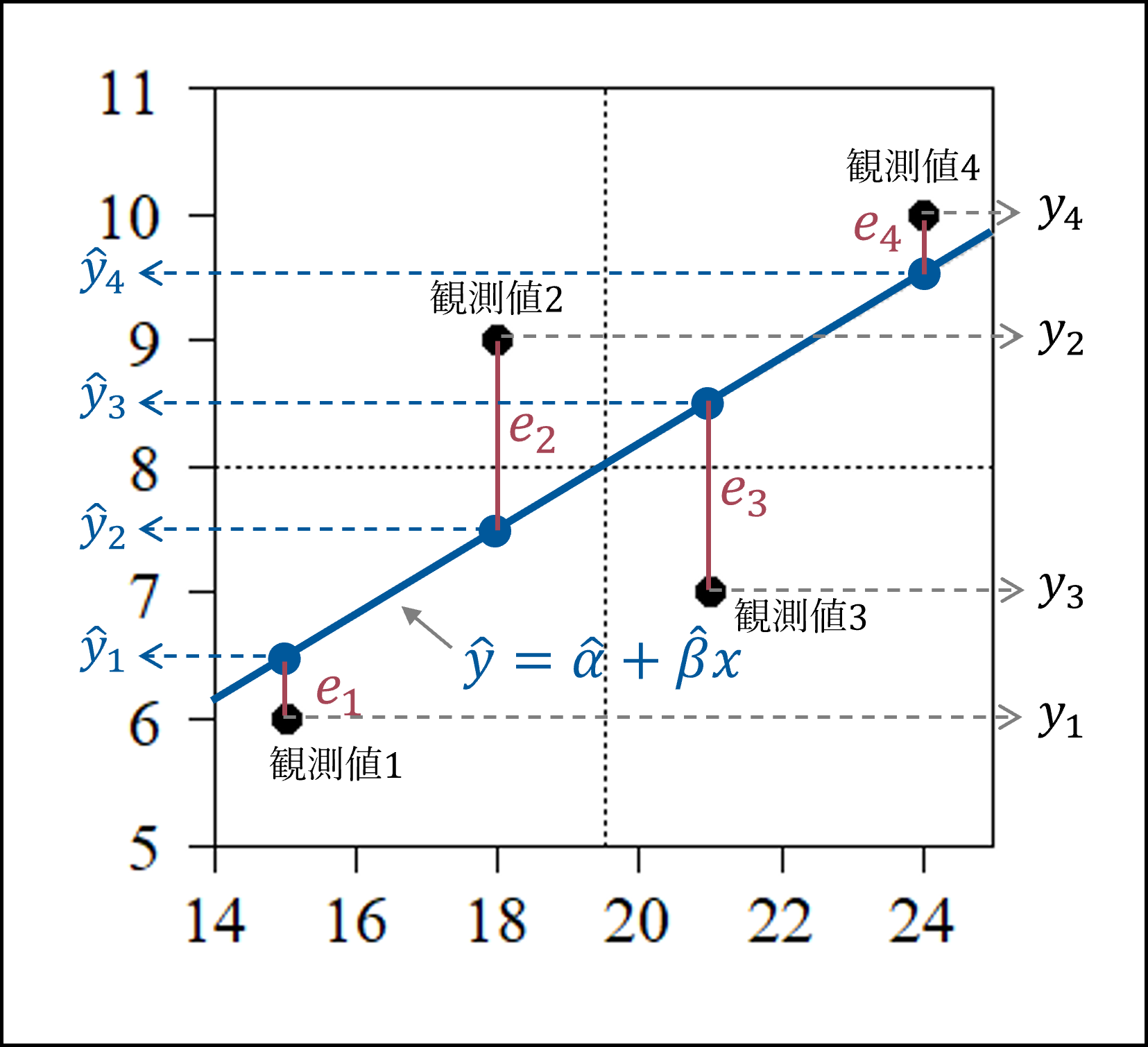
観測値と回帰直線による予測値との差を「残差」と呼びます。また、各観測値の残差を2乗して合計した値を残差平方和と呼びます。

※残差平方和を最小にするように回帰係数を推定する推定方法を最小二乗法と呼びます。
回帰直線を図で確認しておきましょう。赤線で示した残差(の平方和)が最小となるように青線(回帰直線)が推定されます。
(6) 最小二乗法
最小二乗法により推定される回帰係数は以下の式となります。

最小二乗法により推定された回帰直線(定数項と傾きをもつ)は以下の性質を持ちます。

(再掲:回帰直線の図↓)

全体平方和に対する回帰平方和の割合を決定係数と呼びます。決定係数は回帰直線の「説明力」を表します。
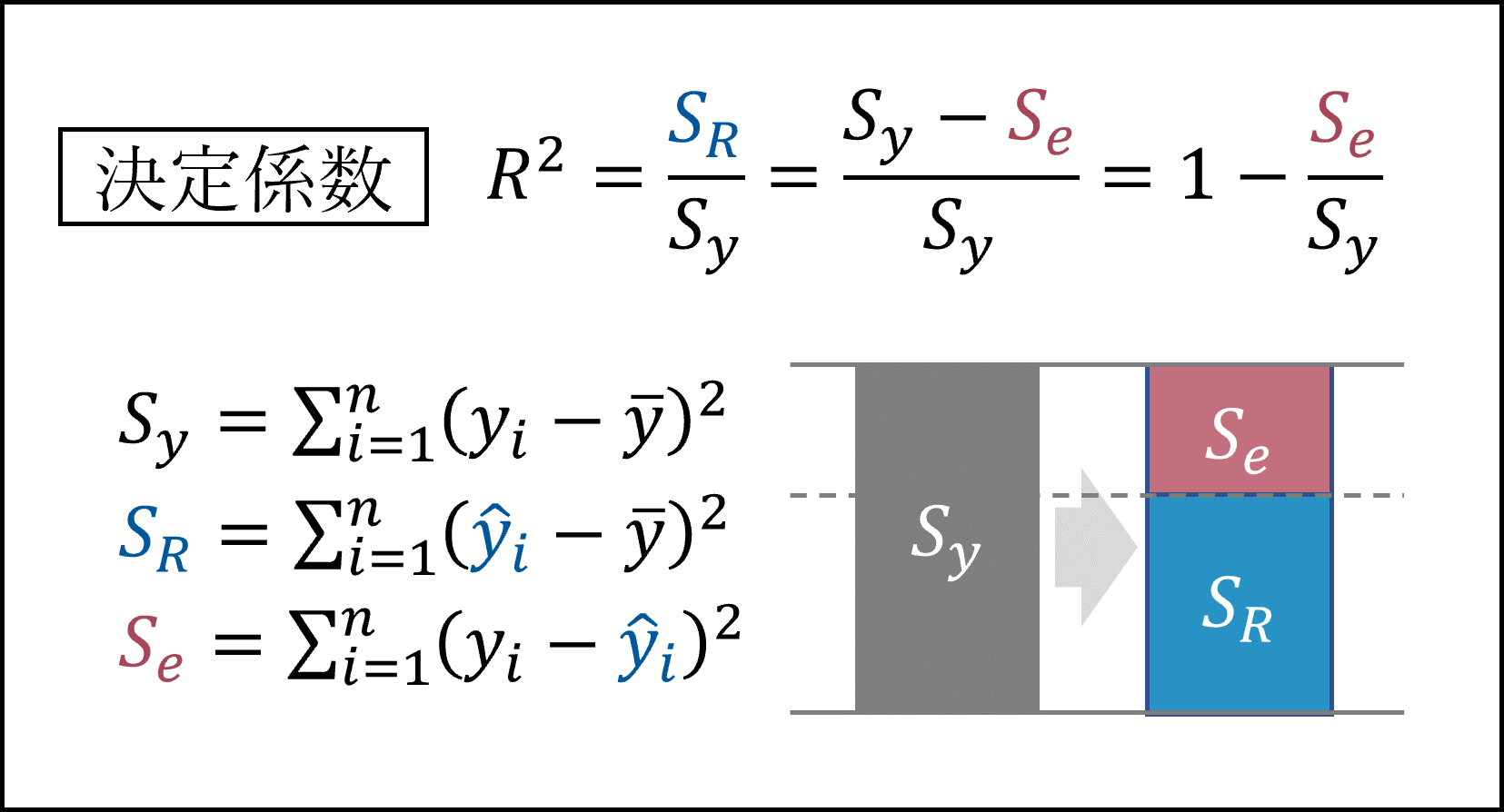
※重回帰モデルで扱う「自由度調整済み決定係数」とあわせて確認しておきましょう。
(7) 時系列データと指数
一定期間(T期間)の変化率は、T期間の変化率の幾何平均により計算します。
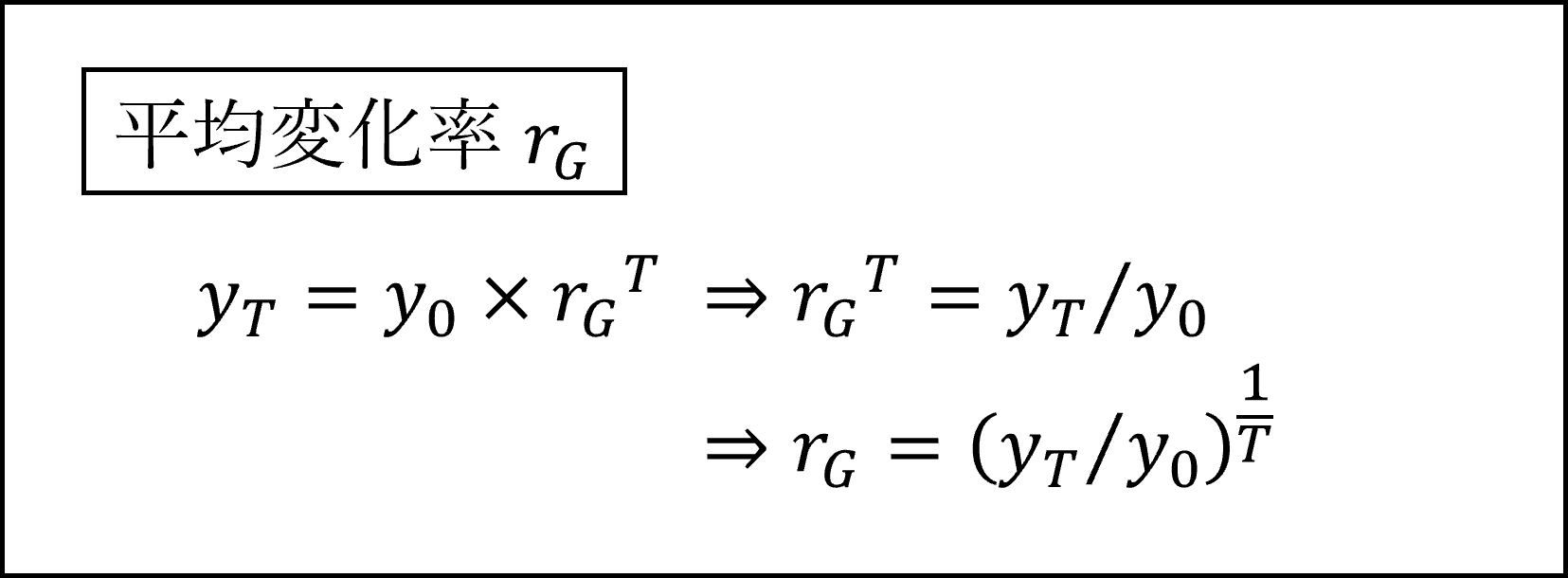
時系列データの周期的な変動を以下のように分解する考え方があります。

コレログラムは横軸にラグ(時間差、時間のズレ)、縦軸に自己相関係数をとったグラフになります。
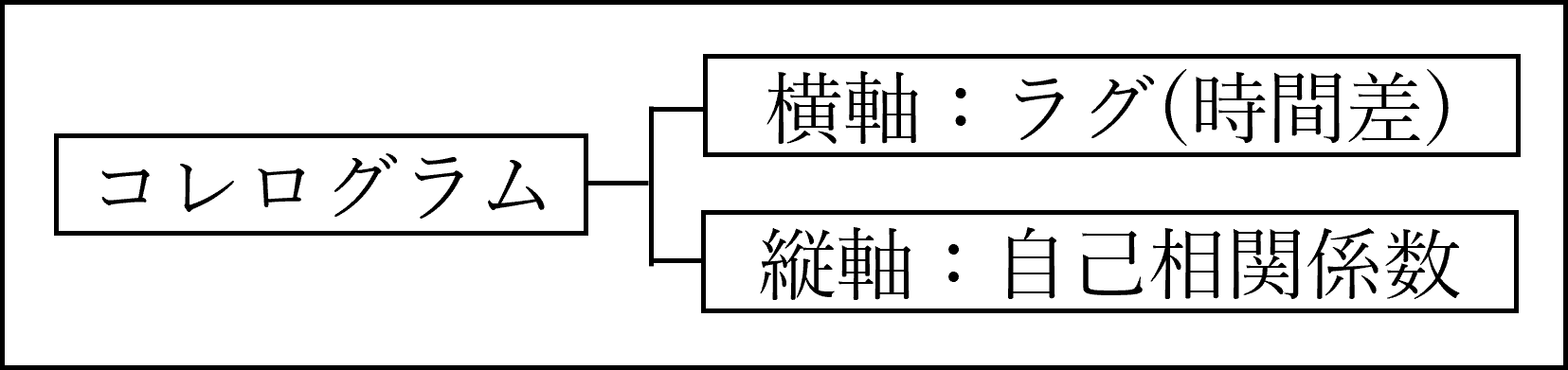
コレログラムの図の例を見ておきましょう。横軸がラグ、縦軸が自己相関係数です。
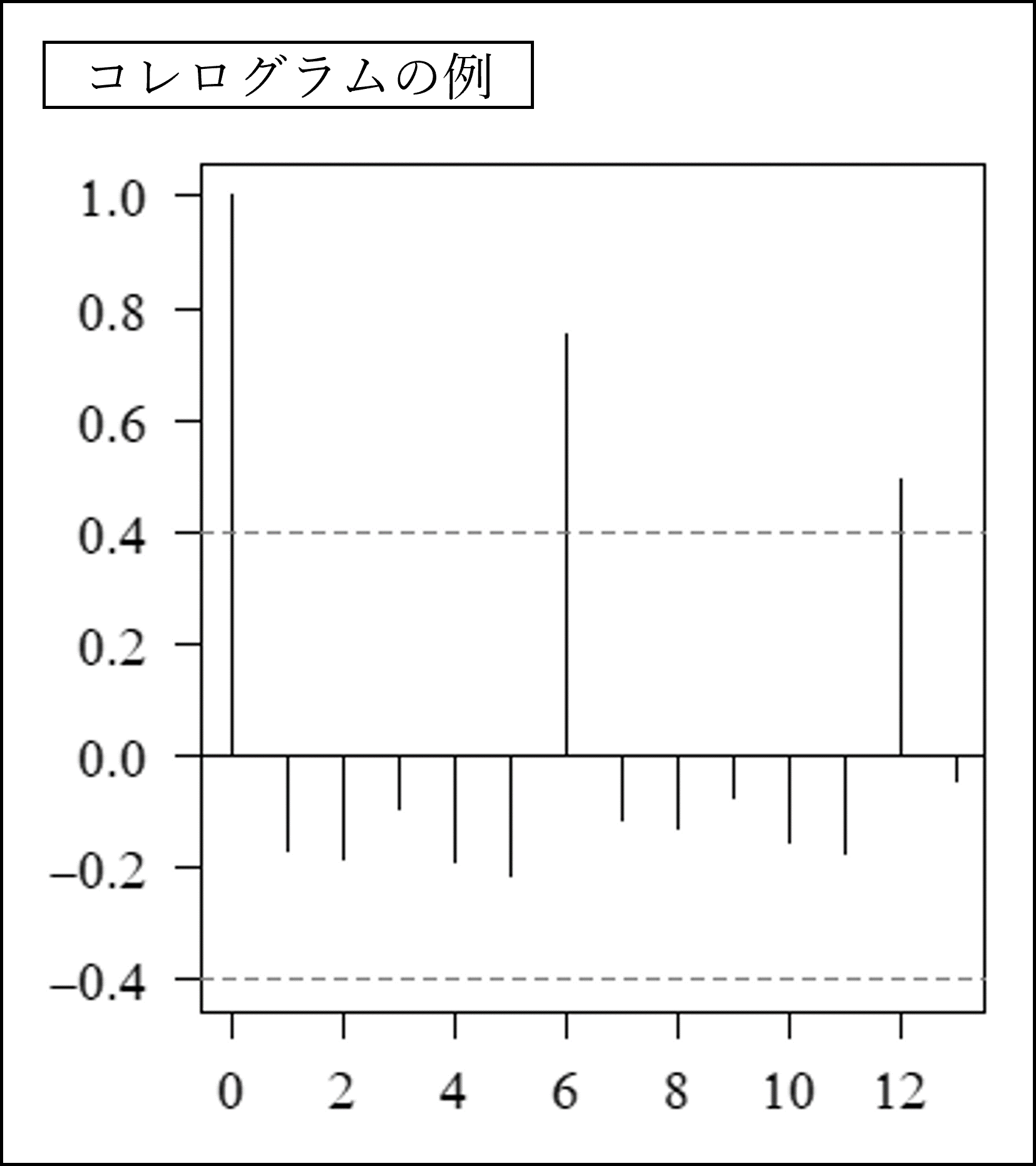
上記は毎月の賃金(半年ごとの賞与を含む)データをイメージして作成した架空のデータのコレログラムです。コレログラムからラグが6、12(ヶ月)のときに正の自己相関があることを確認できます。
異なる時点間の価格を比較するために「価格指数」が用いられます。価格指数の代表的な計算方法としてラスパイレス式とパーシェ式があります。
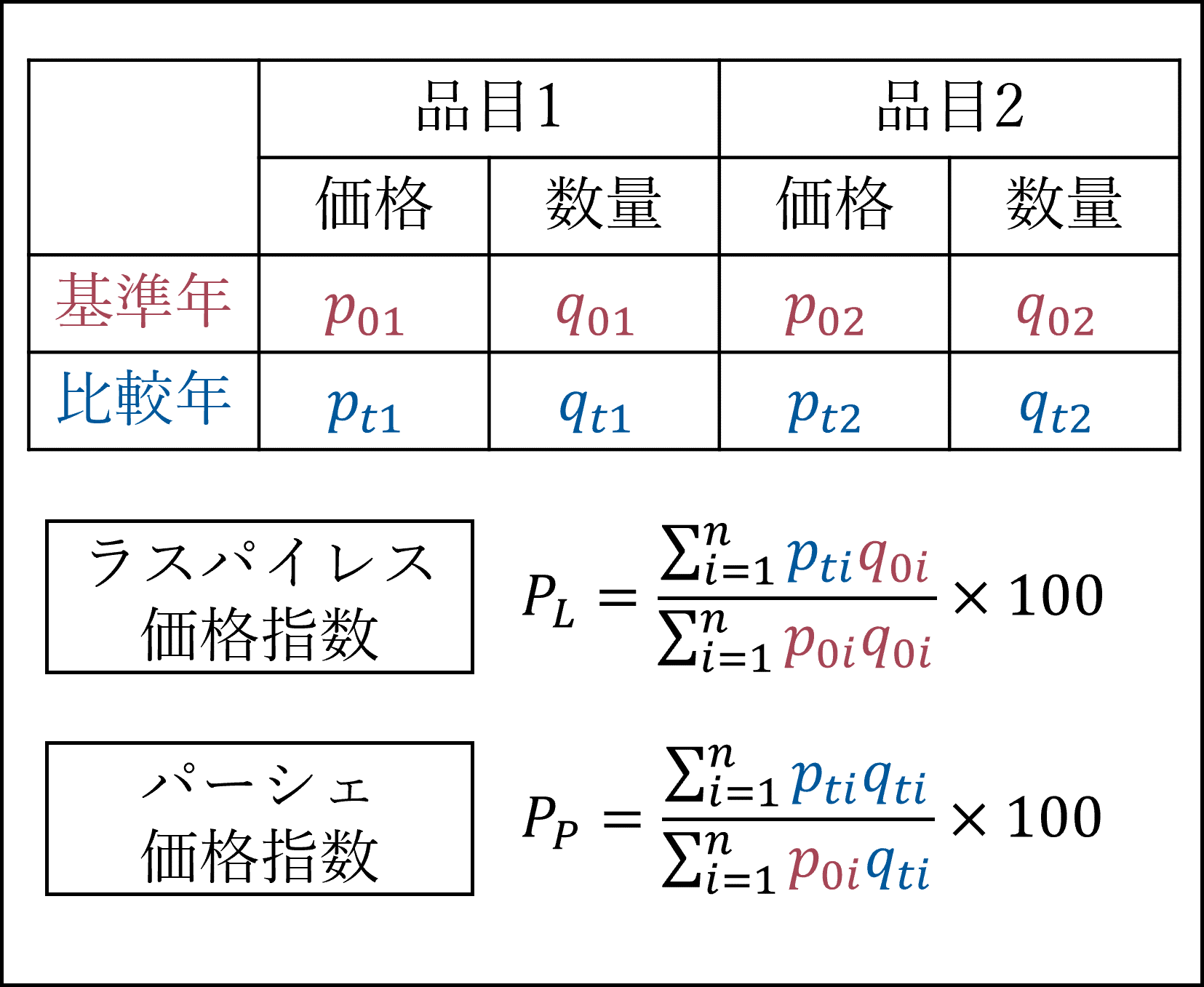
※ラスパイレス価格指数とパーシェ価格指数の計算例

(「記述統計」は以上です)
統計学を学習されている方々に届くように
ぜひシェアをお願いします!

