準1級文系解説について(各回共通)
ご訪問いただきありがとうございます。こちらは統計検定🄬準1級合格を目指す方が、公式テキスト『統計学実践ワークブック』やそのほか統計検定🄬準1級対策コンテンツをスラスラと学び進めるために必要な解説を行うブログです。
本ブログは、公開されている「統計検定🄬準1級出題範囲」の各項目について執筆しています。「統計検定🄬準1級出題範囲」は『統計学実践ワークブック』の内容にも対応していますので、本ブログの解説が『統計学実践ワークブック』の読解に役立つ部分も多くあるかと思います。その意味で、本ブログをご覧いただく方には、公式テキスト『統計学実践ワークブック』を購入されることを推奨いたします。
なお、統計検定🄬は一般財団法人統計質保証協会の登録商標です。また、本ブログは一般財団法人統計質保証協会から公認されたコンテンツではありません。
00. はじめに
「正規分布に従う確率変数 \(X\) の、2乗( \(X^{2}\) )はどんな分布になる?」
「指数分布に従う2つの確率変数を足し合わせたら、その『和』はどんな分布になる?」
統計学を学んでいると、すでにある確率変数( \(X\) )を加工して、新しい確率変数( \(Y\) )を作りたくなる場面が頻繁に訪れます。しかし、元の確率密度関数が分かっていても、変換後の確率密度関数を求めるのは一筋縄ではいきません。
この問題を解決するためのテクニックが、今回学ぶ「変数変換」です。この記事を通して、準1級の対策として不可欠な以下の内容について理解を深めていきましょう。
- 変数変換の本質:確率の「面積」を保つための「密度の調整」という核心的なアイデア
- 1次元の変数変換:変換の基本となる公式を、逆関数・導関数の意味からしっかり理解する
- 2次元の変数変換:2次元の変数変換において登場する「ヤコビアン」を、「面積の変化率」という直感的なイメージでゼロから理解する
特に「ヤコビアン」は、多くの人が意味も分からず公式を丸暗記しようとして挫折する最難関ポイントです。しかし、「面積の変化率」という観点から意味を確認することでグッと理解しやすくなるはずです。この記事で、ヤコビアンの壁を一緒に乗り越えていきましょう!
01. 変数変換とは
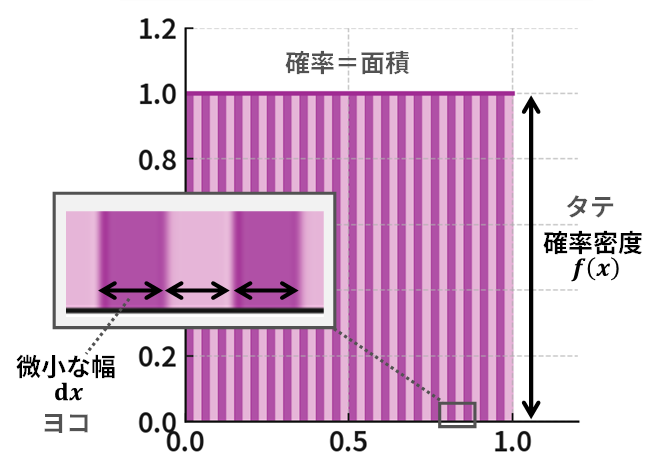
変数変換を理解するための最も重要なキーワードは「密度の調整」です。確率密度関数において、確率は「面積」で表現されました。具体的には以下の図のように、その値における「確率の密度 \(f(x)\) 」に極めて小さい「微小な幅 \(\mathrm{d}x\) 」を掛け合わせることで、確率が導かれます。つまり、確率は「密度×幅」を集めたものということです。
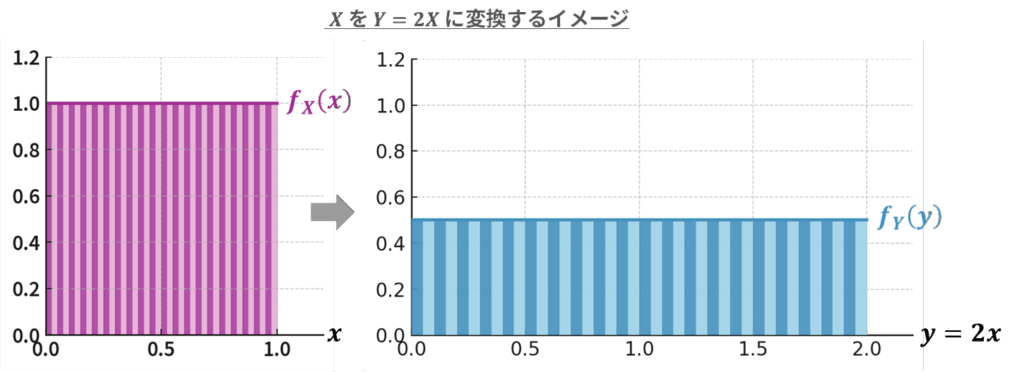
変数変換を行うと、上記の横軸の「幅」が伸びたり縮んだりします。例えばいま、確率変数 \(X\) を2倍して確率変数 \(Y=2X\) に変換するとします。このとき、 \(Y\) の1目盛りは、\(X\) の1目盛りの2倍の幅を持つことになります。この「2倍の幅」をそのまま元の「確率の密度」に掛け合わせてしまうと、面積(確率)が2倍になってしまい、面積の合計が1を超えることになってしまいます。そこで、幅が2倍に伸びたときには、それに対応する「確率の密度」を2分の1に圧縮して、面積が変わらないように調整する必要があるのです。
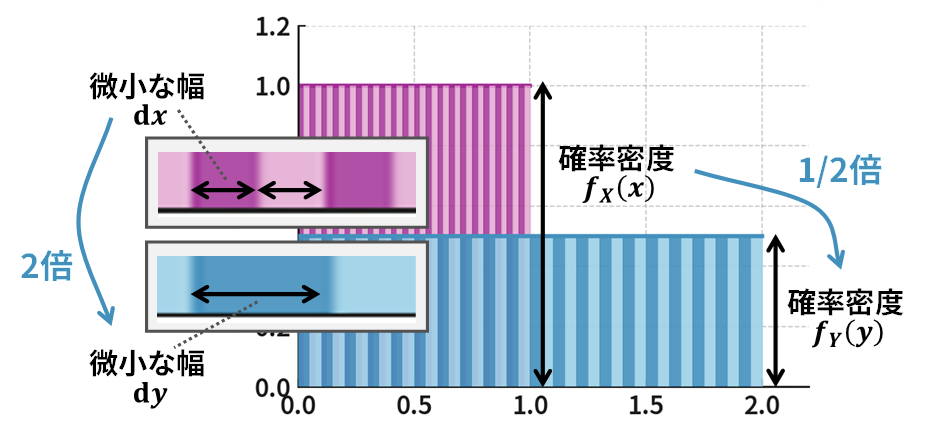
この「伸び縮みした分だけ、密度を逆数倍して調整する」というのが、変数変換の根本的なアイデアです。
02. 1次元の変数変換
変数変換の公式
確率変数 \(X\) の確率密度関数を \(f_{X}(x)\) 、新しい確率変数 \(Y=g(X)\) の確率密度関数を \(f_{Y}(y)\) とします。例えば、確率変数 \(X\) が 0〜1 の範囲で等しい確率(確率密度 \(f_{X}(x)=1\) )をもつとします。このとき、新しい確率変数を \(Y=g(X)=2X\) と定義すると、 \(Y\) は 0〜2 の値をとります。ここから \(Y\) の確率密度関数 \(f_{Y}(y)\) をどのように導くか、というのがこれからのテーマです。
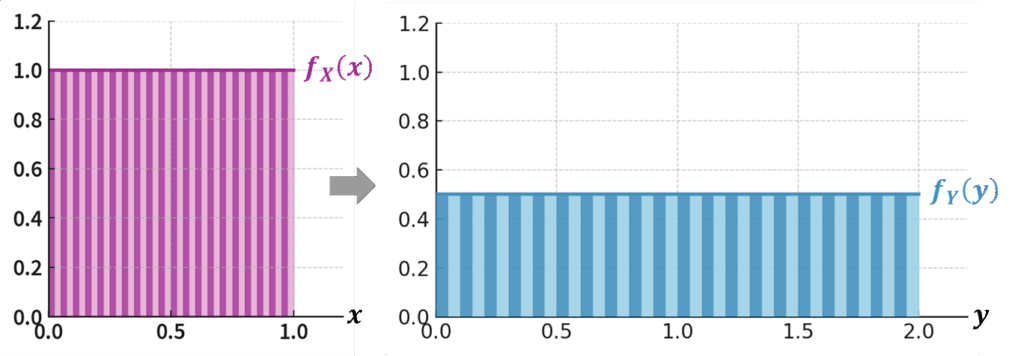
このとき、\(f_{Y}(y)\) は以下の公式で求められます。
\[\begin{align*}
f_{Y}(y) &= \frac{f_X(x)}{\left| \mathrm{d}y/\mathrm{d}x \right|} = \frac{f_{X}(x)}{\left| g'(x) \right|} \\[6pt]
&= \frac{f_{X}\!\left(g^{-1}(y)\right)}{\left| g’\!\left(g^{-1}(y)\right) \right|}
\end{align*}\]
この式を分子と分母に分解し、それぞれが何を示しているのか解読しましょう。
分子の解釈
\[\begin{align*}
f_{Y}(y) &= \frac{\colorbox{lightyellow}{$f_X(x)$}}{\left| \mathrm{d}y/\mathrm{d}x \right|} = \frac{\colorbox{lightyellow}{$f_X(x)$}}{\left| g'(x) \right|} \\[6pt]
&= \frac{\colorbox{lightyellow}{$f_{X}\!\left(g^{-1}(y)\right)$}}{\left| g’\!\left(g^{-1}(y)\right) \right|}
\end{align*}\]
- 元の確率密度です。これは「密度(タテ)×幅(ヨコ)」で考えたときのタテに該当するものです。ただし、変換のためには、 \(x\) を \(y\) で表した式(逆関数)を代入する必要があります。
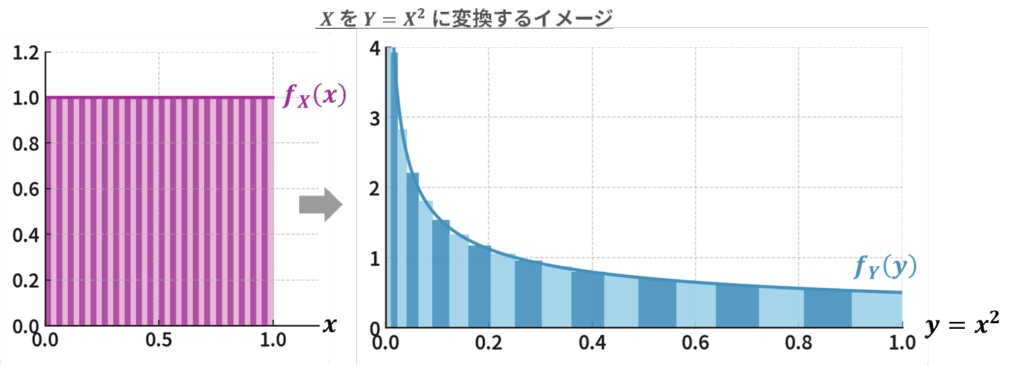
- 例えば、 \(Y=2X\) であれば逆関数は \(X=Y/2\) なので、 \(f_{X}(y/2)\) となります。仮に、 \(Y=X^{2}\) であれば逆関数は \(X=\sqrt{\rule{0pt}{2ex}Y}\, , -\sqrt{\rule{0pt}{2ex}Y}\) という2つの値となります。そのため、\(f_{X}(x)\) に逆関数を代入するときは \(f_{X}(\sqrt{\rule{0pt}{2ex}Y})\) と \(f_{X}(-\sqrt{\rule{0pt}{2ex}Y})\) の2つをあわせて考慮する必要があります。
- 一般的には、逆関数 \(x=g^{-1}(y)\) を代入するということなので、以下のように表記します。
\[ f_{X}(x)\;\to\;f_{X}\bigl(g^{-1}(y)\bigr) \]
分母の解釈
\[\begin{align*}
f_{Y}(y) &= \frac{f_X(x)}{\colorbox{lightyellow}{$\left| \mathrm{d}y/\mathrm{d}x \right|$}} = \frac{f_{X}(x)}{\colorbox{lightyellow}{$\left| g'(x) \right|$}} \\[6pt]
&= \frac{f_{X}\!\left(g^{-1}(y)\right)}{\colorbox{lightyellow}{$\left| g’\!\left(g^{-1}(y)\right) \right|$}}
\end{align*}\]
- これが「密度の調整」を行う部分で、「 \(x\) の微小な幅 \(\mathrm{d}x\) 」に対する「 \(y\) の微小な幅 \(\mathrm{d}y\) 」の伸び率を意味しています。つまり、「密度(タテ)×幅(ヨコ)」で考えたときのヨコの伸び率です。このヨコの伸び率を分母におくことで、タテの確率密度を割り戻し、「密度×幅」の合計(=確率)が1となるように密度に調整をかけています。
- なお、\(\mathrm{d}y/\mathrm{d}x\) は「 \(x\) をごくわずかに変化させたとき、 \(y\) がどれくらいの割合で変化するか」という変化率(傾き)を表します。この変化率を「 \(y\) の \(x\) による微分」あるいは「導関数」と呼び、関数 \(g\) の導関数はダッシュ記号を付して \(\mathrm{d}y/\mathrm{d}x=g'(x)\) とも書きます。導関数は高校数学で学ぶ微分公式によって導出します(統計検定準1級で最低限必要な微分公式は別途)。
- 例えば、\(Y=2X\) であれば \(g(x)=2x\) なので、これを微分すると \(g'(x)=2\) となります。つまり、\(x\) から \(y\) に変換することでヨコが \(2\) 倍になるので、これを割り戻すことで \(Y\) の確率密度に変換します。
- 仮に、\(Y=X^{2}\) であれば \(g(x)=x^{2}\) なので、これを微分すると \(g'(x)=2x\) となります。つまり、\(x\) から \(y\) に変換することでヨコが \(2x\) 倍になるので、これを割り戻すことで \(Y\) の確率密度に変換します。このとき \(g'(x)=2x\) をそのまま用いると \(x\) が残ってしまいますので、この \(x\) に逆関数 \(x=g^{-1}(y)\) を代入する必要があります。これを踏まえ一般化すると、 \(g’\!\left(g^{-1}(y)\right)\) という表記になります。
- なお、絶対値 \(\left|\cdots\right|\) が付いているのは、確率密度は必ずプラスの値である必要があることから、伸び縮みの「大きさ」だけを問題にするためです。
微分公式については以下の記事でご紹介しています。高校数学で習う微分公式が整理されていますので、微分公式に不安がある方はお読みください。
例題
変数変換は具体例で実際に計算してみないともやもやが残りやすいです。以下に例題を用意しましたので、ぜひ取り組んでみてください。
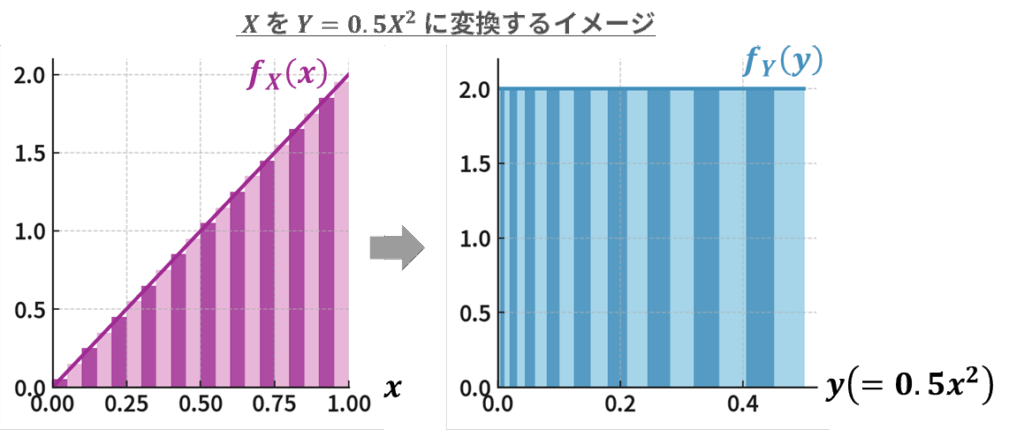
【例題】確率変数 \(X\) が0〜1の範囲の値をとり、その確率密度関数は \(f_{X}(x)=2x\) とします。このとき、確率変数 \(Y=g(X)=0.5X^{2}\) の確率密度関数 \(f_{Y}(y)\) を導いてください。
【答え】問題文から \(y\) を \(x\) で表す関数は \(y=g(x)=0.5x^{2}\) で、その逆関数( \(x\) を \(y\) で表す関数)は \(x=g^{-1}(y)=\sqrt{2y}\) となります( \(x\) は0~1の範囲の値なので正の場合のみを考慮しています)。また、関数 \(g(x)\)の導関数は微分公式より \(g'(x)=x\) となります。これらを変数変換の公式に代入すると、以下のように \(Y\) の確率密度関数 \(f_{Y}(y)\) を導くことができます。
\[\begin{align*}
f_{Y}(y) &= \frac{f_{X}\!\left(g^{-1}(y)\right)}{\left| g’\!\left(g^{-1}(y)\right) \right|}
= \frac{f_{X}\!\left(\sqrt{2y}\right)}{\left| g’\!\left(\sqrt{2y}\right) \right|}\\[6pt]
&= \frac{2\sqrt{2y}}{\left| \sqrt{2y} \right|} = 2 \; (0 < y < 0.5)
\end{align*}\] なお、\(y\) の範囲が、元の \(x\) の範囲 \((0<x<1)\) に対応する \((0<y<0.5)\) 以外の値をとることはありません。そのためこの区間外では \(Y\) が現れる確率は \(0\) であり、確率密度も \(f_{Y}(y)=0\) となります。
03. 2次元の変数変換とヤコビアン
さて、いよいよ難関のヤコビアンです。変数が2つ \((X,\,Y)\) になり、新しい変数 \((Z,\,W)\) に変換する場合を考えます。ここでは元の変数 \((X,Y)\) から何らかの関数 \(u,v\) を使って新しい変数 \((Z,W)\) を \((Z,W)=\bigl( u(X,Y), \, v(X,Y) \bigr)\) のように変換できる場合を考えます。1次元では「幅」の伸び縮みを考えましたが、2次元では「面積」の伸び縮みを考える点がポイントです。
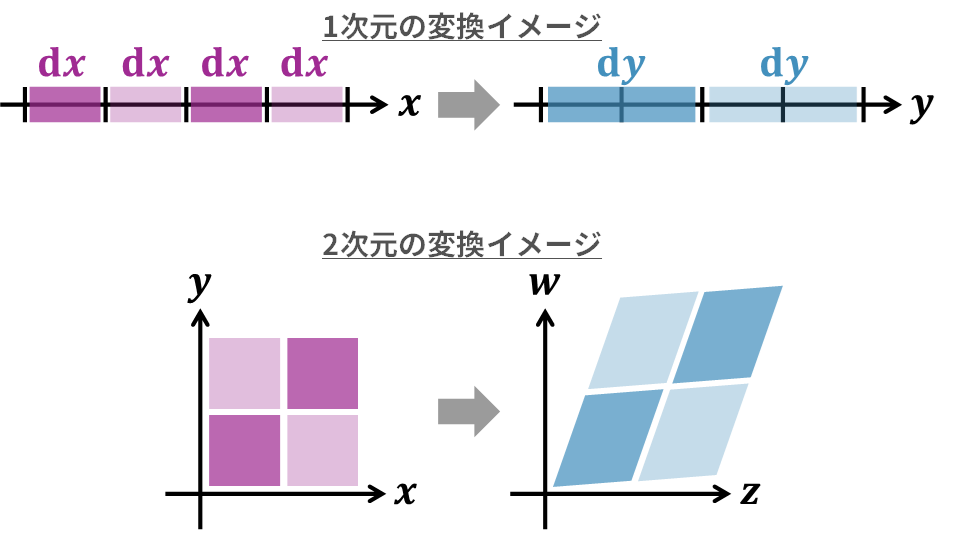
ここで、\((X,\,Y)\) 平面上の微小な正方形は、変換によって、\((Z,\,W\)) 平面上では平行四辺形に歪んで移されます。このとき、元の正方形と、変換後の平行四辺形の「面積の比率」が、2次元における「密度の調整項」になります。この「面積の拡大・縮小率」を計算してくれる便利な道具がヤコビアン (Jacobian) です。
ヤコビアンとは
ヤコビアンとは、元の \((X, Y)\) 平面から新しい \((Z, W)\) 平面へ変換する際の、局所的な面積の変化率を求めるための道具です。具体的にはヤコビアンを \(J(X,Y)\) と表記し、以下の式で表します。
\[ J(X,Y) = \dfrac{\partial(Z, W)}{\partial(X, Y)} \]
分母の \(\partial(X,Y)\) は「元の \((X,Y)\) 平面の微小な大きさ」を意味し、分子の \(\partial(Z,W)\) は「変換後の \((Z,W)\) 平面の微小な大きさ」を意味しています。つまり、ヤコビアン \(J(X,Y)\) は「 \((x,y)\) をごくわずかに変化させたとき、 \((z,w)\) がどれくらいの割合で変化するか」という変化率を表します。
そしてこの変化率が以下の「行列式」というものによって計算されます。\(\mathrm{det}\) は「determinant(行列式)」の略で、「この行列の行列式を求めよ」という指示を表しています。なお、2つ目の「=」では新しい変数を \((Z,W)=\bigl( u(X,Y), \, v(X,Y) \bigr)\) として展開しています。
\[ \begin{align*}
J(X,Y) &= \det
\begin{pmatrix}
\dfrac{\partial Z}{\partial X} & \dfrac{\partial Z}{\partial Y}\\[6pt]
\dfrac{\partial W}{\partial X} & \dfrac{\partial W}{\partial Y}
\end{pmatrix}\\[10pt]
&= \det
\begin{pmatrix}
\dfrac{\partial u(X,Y)}{\partial X} & \dfrac{\partial u(X,Y)}{\partial Y}\\[6pt]
\dfrac{\partial v(X,Y)}{\partial X} & \dfrac{\partial v(X,Y)}{\partial Y}
\end{pmatrix}
\end{align*} \]
上記の行列を構成する4つの成分は、\((X,Y)\) から \((Z,W)\) への変換に関する偏導関数を意味しています。偏導関数は1次元ずつ部分的に切り取って変化を測るものです。すなわち、元の変数 \((X,Y)\) について他方の変数を一定に保ったまま一方の変数を微小に変化させたときに、\(Z\) や \(Y\) がどのように変化するかを示します。
- \(\dfrac{\partial Z}{\partial X}\): 関数 \(Z=u(X,Y)\) の \(X\) についての偏微分。つまり、 \(Y\) を一定に保ったまま \(X\) を微小に変化させたとき、\(Z\) がどれくらい変化するかを示す「\(X \to Z\)」の変化率 \(\cdots (a)\)
- \(\dfrac{\partial Z}{\partial Y}\): 関数 \(Z=u(X,Y)\) の \(Y\) についての偏微分。つまり、 \(X\) を一定に保ったまま \(Y\) を微小に変化させたとき、\(Z\) がどれくらい変化するかを示す「\(Y \to Z\)」の変化率 \(\cdots (b)\)
- \(\dfrac{\partial W}{\partial X}\):関数 \(W=v(X,Y)\) の \(X\) についての偏微分。つまり、 \(Y\) を一定に保ったまま \(X\) を微小に変化させたとき、\(W\) がどれくらい変化するかを示す「\(X \to W\)」の変化率 \(\cdots (c)\)
- \(\dfrac{\partial W}{\partial Y}\):関数 \(W=v(X,Y)\) の \(Y\) についての偏微分。つまり、 \(X\) を一定に保ったまま \(Y\) を微小に変化させたとき、\(W\) がどれくらい変化するかを示す「\(Y \to W\)」の変化率 \(\cdots (d)\)
ヤコビアンの視覚的理解
さて、いま確認したいのは元の \((X, Y)\) 平面から新しい \((Z, W)\) 平面へ変換する際の「面積の変化率」です。ここで、元の \((X,Y)\) 平面の \(X\) 軸と \(Y\) 軸のうち、\(X\) 軸のみに着目してみます。そして、この \(X\) 軸から新しい \((Z,W)\) 平面への変換を考えたいのですが、 \(X\) 軸が1次元であるのに対して、新しい \((Z,W)\) 平面は2次元であり、次元が異なります。そこで、\(X\) という1つの軸が、新しい \((Z,W)\) 平面でどのような向きを持つかを整理しておく必要があります。
この新しい \((Z,W)\) 平面における \(X\) の向きを考えるために役立つのが、ヤコビアンの行列の1列目を構成する2つの成分になります。具体的には、「\(X \to Z\) の変化率: \(\partial Z / \partial X\) 」を \(Z\) 軸の座標、と「\(X \to W\) の変化率: \(\partial W / \partial X\) 」を \(W\) 軸の座標とみなすことができます。この座標で示される向きこそが、 \(X\) 軸を \((Z,W)\) 平面に「埋め込んだ」結果となります。
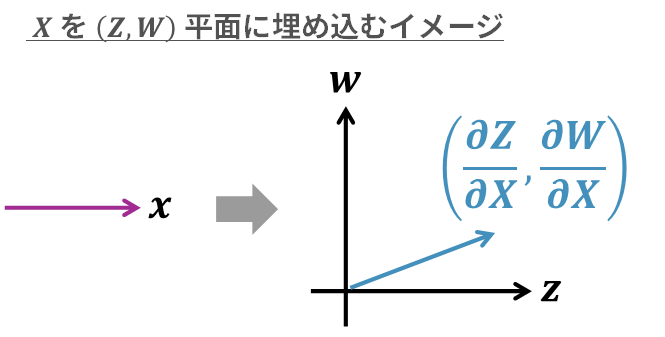
同様に、新しい \((Z,W)\) 平面における \(Y\) の向きは、ヤコビアンの行列の2列目を構成する2つの成分で示されます。具体的には、「\(Y \to Z\) の変化率: \(\partial Z / \partial Y\) 」を \(Z\) 軸の座標、「\(Y \to W\) の変化率: \(\partial W / \partial Y\) 」を \(W\) 軸の座標とみなすことができます。この座標で示される向きが、 \(Y\) 軸を \((Z,W)\) 平面に「埋め込んだ」結果となります。

これを踏まえると、元の \((X,Y)\) 平面は、新しい \((Z,W)\) 平面に、以下のように「埋め込まれる」ことになります。これはつまり、ヤコビアンの行列の各列で示される2つのベクトルによって作られる平行四辺形を意味しています。
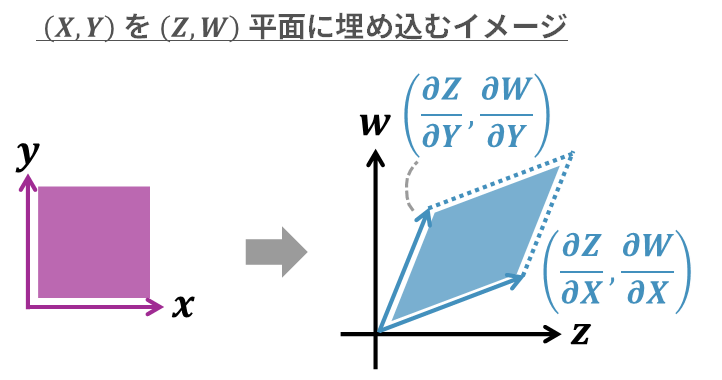
ここで、元の \((X,Y)\) 平面における「微小な大きさ(面積)」を1とすると、新しい \((Z,W)\) 平面に埋め込まれた平行四辺形の面積は、この変数変換による「面積の変化率」を意味します。そして、この平行四辺形の面積を求める計算式こそがヤコビアンの「行列式 \(\mathrm{det}\) 」という計算なのです。
\[
J(X,Y) = \det
\begin{pmatrix}
\colorbox{lightblue}{$\dfrac{\partial Z}{\partial X}$} & \colorbox{lightcyan}{$\dfrac{\partial Z}{\partial Y}$}\\[6pt]
\colorbox{lightblue}{$\dfrac{\partial W}{\partial X}$} & \colorbox{lightcyan}{$\dfrac{\partial W}{\partial Y}$}
\end{pmatrix}
\]
つまり、ヤコビアンの行列式は、行列の「列ベクトルで作られる平行四辺形の面積」を意味します。行列式がなぜ平行四辺形の面積と等しくなるのかについては別記事で詳しくご紹介しますが、ここではまず以下の行列式の計算方法を覚えておきましょう。
\[\begin{align*}
\det \begin{pmatrix}
\colorbox{lightsalmon}{$ a $} & \colorbox{lightyellow}{$ b $} \\
\colorbox{lightyellow}{$ c $} & \colorbox{lightsalmon}{$ d $} \end{pmatrix}
&= \colorbox{lightsalmon}{$ a \times d $} \; – \; \colorbox{lightyellow}{$ b \times c $}\\
&= \colorbox{lightsalmon}{$ ad $} \; – \; \colorbox{lightyellow}{$ bc $}
\end{align*}\]
行列式は上記のように「斜めに掛けて引き算」することで計算されます。具体的には、「左上と右下の成分の積」から「右上と左下の成分の積」を引くことで導かれます。この計算がなぜ2つのベクトルで作られる平行四辺形の面積と等しくなるのか気になるところですが、多くの紙面を必要としますので、以下の別記事にて詳しくご紹介させていただきます。ここでは本題の「2次元の変数変換」について先に進んでいきましょう。

2次元の変数変換の公式
2つの確率変数 \((X,\,Y)\) を新しい確率変数 \((Z,\,W)\) に変換するとき、元の確率変数についての確率密度関数を \(f_{X,Y}(x,y)\) とし、変換後の新しい確率変数についての確率密度関数を \(f_{Z,W}(z,w)\) とすると、変換後の確率密度関数は以下の式で導くことができます。
\[ f_{Z,W}(z,w) = \frac{f_{X,Y}(x,y)}{\left| J(x,y) \right|} \]
なお、元の変数 \((X,Y)\) から関数 \(u,v\) を使って新しい変数を \((Z,W)=\bigl( u(X,Y), \, v(X,Y) \bigr)\) のように変換できるものとし、また、 \((Z,W)\) が与えられれば元の \((X,Y)\) を一意に決められるものとします。したがって、上記の右辺の関数 \(f_{X,Y}(x,y)\) やヤコビアン \(J(x,y)\) の \((x,y)\) は、与えられた \((z,w)\) から一意的に求めた元の変数 \((X,Y)\) の値を意味します。
これについても、1次元のときと同様に、分子と分母に分解して考えてみましょう。
分子の解釈
\[ f_{Z,W}(z,w) = \frac{\colorbox{lightyellow}{$f_{X,Y}(x,y)$}}{\left| J(x,y) \right|} \]
元の確率変数 \((X,Y)\) の確率密度関数です。基本的にはこの確率密度関数が、変換後の確率変数 \((Z,W)\) の確率密度関数の「もと」となります。ただし、変換のためには、元の \((X,Y)\) を変換後の \((Z,W)\) で表す必要があります。
分母の解釈
\[ f_{Z,W}(z,w) = \frac{f_{X,Y}(x,y)}{\colorbox{lightyellow}{$\left| J(x,y) \right|$}} \]
これは \((X,Y)\) から \((Z,W)\) への変換に対するヤコビアンです。先ほどみてきたとおり、具体的には、元の変数 \((X,Y)\) から \((Z,W)\) に変換したときの「面積の変化率」を表します。この変化率を分母におくことで、元の確率密度関数を割り戻し、確率の合計が1となるように調整をかけています。
なお、分子と同様、変換のためには元の \((X,Y)\) を変換後の \((Z,W)\) で表す必要があります。
また、絶対値が付いているのは、確率密度は正の値をとることから、変化率の「大きさ」のみを考慮するためです。
例題
2次元の変数変換も、実際に例題を解いてみないとモヤモヤが残ります。以下にシンプルな例題を用意しましたのでぜひ取り組んでみてください。
【例題】確率変数 \(X,Y\) は互いに独立に一様分布 \(U(0,1)\) に従うものとし、その確率密度関数は以下の通りです。
\[ f_{X,Y}(x,y) =
\begin{cases}
1 & (0<x<1,\; 0<y<1)\\
0 & \text{それ以外}
\end{cases} \]
ここで、新しい変数 \((Z,W)\) を以下のように定義します。
\[\begin{align*} Z&=X+Y\\ W&=X-Y\end{align*}\]
このとき、「①ヤコビアン \(J(x,y)\) 」と「②変換後の確率密度関数 \(f_{Z,W}(z,w)\) 」を導いてください。
【答え】① \((X,Y)\) から \((Z,W)\) への変換に対するヤコビアンは以下の式で導かれます。
\[ J(X,Y) = \det
\begin{pmatrix}
\dfrac{\partial Z}{\partial X} & \dfrac{\partial Z}{\partial Y}\\[6pt]
\dfrac{\partial W}{\partial X} & \dfrac{\partial W}{\partial Y}
\end{pmatrix} \]
ここで、\(z=x+y\) について \(x\) の偏微分は \(1\) となり、 \(y\) の偏微分も \(1\) となります。また、 \(w=x-y\) について \(x\) の偏微分は \(1\) となり、 \(y\) の偏微分は \(-1\) となります。したがって、ヤコビアンを以下のように整理できます。
\[\begin{align*}
J(X,Y) &= \det \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\\[3pt]
&= 1 \times (-1) \; – \; 1 \times 1\\[3pt]
&= -2 \end{align*} \]
②の変換後の確率密度関数 \(f_{Z,W}(z,w)\) は、変数変換の公式と上記で求めたヤコビアンの値により、以下のように導かれます。
\[ \begin{align*}
f_{Z,W}(z,w)&=\dfrac{f_{X,Y}(x,y)}{\left| J(x,y) \right|}\\[6pt]
&=\dfrac{1}{\left| -2 \right|}=\dfrac{1}{2} \end{align*} \]
ただし、このとき \(0<x<1 \, , \, 0<y<1\) であるので、\((z,w)\) の領域は以下のように整理されます。なお、与えられた \(z=x+y\) と \(w=x-y\) から、\(2x=z+w\) 、\(2y=z-w\) であることに注意しましょう。
\[ 0<z+w<2 \\[6pt] 0<z-w<2 \]
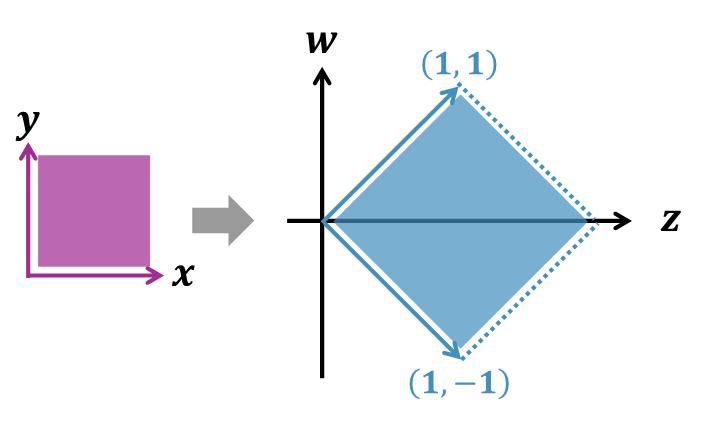
以上の内容をまとめると、変換後の確率密度関数 \(f_{Z,W}(z,w)\) は以下のようになります。
\[
f_{Z,W}(z,w) =
\begin{cases}
\dfrac{1}{2} & (0 < z + w < 2,\; 0 < z \; – \; w < 2)\\[4pt]
0 & \text{それ以外}
\end{cases}
\]
04. 腕試し!模擬問題に挑戦
模擬問題1
模擬問題1:問題
確率変数 \(X\) が0〜1の範囲の値をとり、その確率密度関数は \(f_{X}(x)=3x^{2}\) とします。このとき、確率変数 \(Y=g(X)=X^{3}\) の確率密度関数 \(f_{Y}(y)\) を導いてください。
模擬問題1:解答
問題文から \(y\) を \(x\) で表す関数は \(y=g(x)=x^{3}\) で、その逆関数( \(x\) を \(y\) で表す関数)は \(x=g^{-1}(y)=y^{1/3}\) となります( \(x\) は0~1の範囲の値なので正の場合のみを考慮しています)。また、関数 \(g(x)\)の導関数は微分公式より \(g'(x)=3x^{2}\) となります。これらを変数変換の公式に代入すると、以下のように \(Y\) の確率密度関数 \(f_{Y}(y)\) を導くことができます。
\[\begin{align*}
f_{Y}(y) &= \frac{f_{X}\!\left(g^{-1}(y)\right)}{\left| g’\!\left(g^{-1}(y)\right) \right|}
= \frac{f_{X}\!\left(y^{1/3}\right)}{\left| g’\!\left(y^{1/3}\right) \right|}\\[6pt]
&= \frac{3(y^{1/3})^{2}}{\left| 3(y^{1/3})^{2} \right|} = 1 \; (0 < y < 1)
\end{align*}\]
なお、\(y\) の範囲が、元の \(x\) の範囲 \((0<x<1)\) に対応する \((0<y<1)\) 以外の値をとることはありません。そのためこの区間外では \(Y\) が現れる確率は \(0\) であり、確率密度も \(f_{Y}(y)=0\) となります。
模擬問題2
模擬問題2:問題
確率変数 \(X,Y\) は互いに独立に一様分布 \(U(0,1)\) に従うものとし、その確率密度関数は以下の通りです。
\[ f_{X,Y}(x,y) =
\begin{cases}
1 & (0<x<1,\; 0<y<1)\\
0 & \text{それ以外}
\end{cases} \]
ここで、新しい変数 \((Z,W)\) を以下のように定義します。
\[\begin{align*} Z&=X+2Y\\ W&=X-2Y\end{align*}\]
このとき、「①ヤコビアン \(J(x,y)\) 」と「②変換後の確率密度関数 \(f_{Z,W}(z,w)\) 」を導いてください。
模擬問題2:解答
① \((X,Y)\) から \((Z,W)\) への変換に対するヤコビアンは以下の式で導かれます。
\[ J(X,Y) = \det
\begin{pmatrix}
\dfrac{\partial Z}{\partial X} & \dfrac{\partial Z}{\partial Y}\\[6pt]
\dfrac{\partial W}{\partial X} & \dfrac{\partial W}{\partial Y}
\end{pmatrix} \]
ここで、\(z=x+2y\) について \(x\) の偏微分は \(1\) となり、 \(y\) の偏微分は \(2\) となります。また、 \(w=x-2y\) について \(x\) の偏微分は \(1\) となり、 \(y\) の偏微分は \(-2\) となります。したがって、ヤコビアンを以下のように整理できます。
\[\begin{align*}
J(X,Y) &= \det \begin{pmatrix} 1 & 2 \\ 1 & -2 \end{pmatrix}\\[3pt]
&= 1 \times (-2) \; – \; 2 \times 1\\[3pt]
&= -4 \end{align*} \]
②の変換後の確率密度関数 \(f_{Z,W}(z,w)\) は、変数変換の公式と上記で求めたヤコビアンの値により、以下のように導かれます。
\[ \begin{align*}
f_{Z,W}(z,w)&=\dfrac{f_{X,Y}(x,y)}{\left| J(x,y) \right|}\\[6pt]
&=\dfrac{1}{\left| -4 \right|}=\dfrac{1}{4} \end{align*} \]
ただし、このとき \(0<x<1 \, , \, 0<y<1\) であるので、\((z,w)\) の領域は以下のように整理されます。なお、与えられた \(z=x+2y\) と \(w=x-2y\) から、\(2x=z+w\) 、\(4y=z-w\) であることに注意しましょう。
\[ 0<z+w<2 \\[6pt] 0<z-w<4 \]
以上の内容をまとめると、変換後の確率密度関数 \(f_{Z,W}(z,w)\) は以下のようになります。
\[
f_{Z,W}(z,w) =
\begin{cases}
\dfrac{1}{4} & (0 < z + w < 2,\; 0 < z \; – \; w < 4)\\[4pt]
0 & \text{それ以外}
\end{cases}
\]


