
ヤコビアンの説明の中で、「行列式は面積の変化率を表す」と出てきました。しかし、「行列式が面積と関係ある?」と思った方も多いのではないでしょうか。この記事では、図を見ながら直感的に理解できるように、行列式と面積の関係をやさしく整理していきます。数式よりもまず、イメージでつかむところから始めましょう。
※厳密な証明をご紹介するものではありません。変数変換の学習のなかで「本当に行列式が平行四辺形の面積なのか?」という疑問に感覚的に答えるための記事になります。
00. まずビジュアルでつかむ
原点から2本の矢印を描いてみます。これらを「ベクトル」と呼びます。
ベクトル \(\mathbf{a}\) と \(\mathbf{b}\) は、向きも長さも自由に取れる矢印です。そして、この2本の矢印をもとにして、平行四辺形を作ることができます。
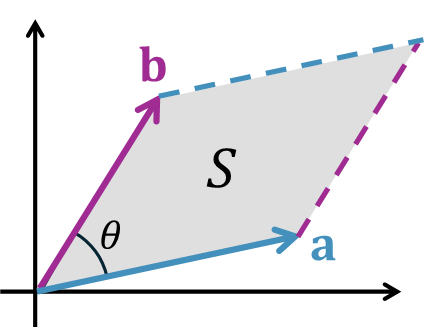
この平行四辺形の「面積」を求めることが、今回のテーマです。というのも、この面積こそが、行列式の「大きさ」と一致するからです。
01. 面積を図形の視点で考える
平行四辺形の面積は、中学校でも習ったように「底辺×高さ」で求められます。ここで、底辺をベクトル \(\mathbf{a}\) の長さ、高さをベクトル \(\mathbf{b}\) か下ろした垂線と考えます。
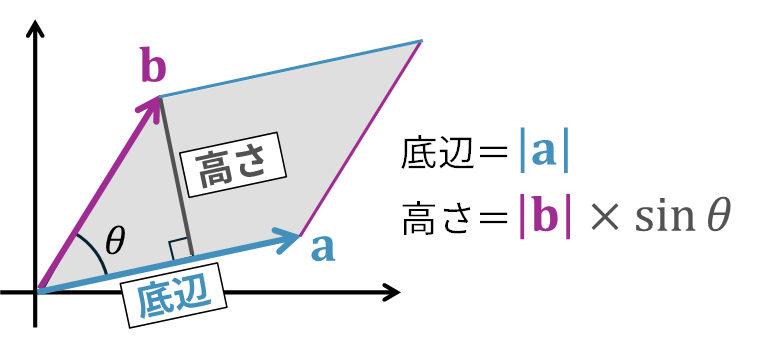
底辺の長さは \(|\mathbf{a}|\) 、高さは \(|\mathbf{b}|\sin\theta\) です。したがって、面積 \(S\) は次のように表せます。
\[
S = |\mathbf{a}| \times |\mathbf{b}| \sin\theta
\]
角度 \(\theta\) が90度なら面積は最大になり、角度が0度に近づくほど面積は小さくなっていきます。2本のベクトルが重なれば、面積はゼロになります。
つまり、平行四辺形の面積は「2本の矢印の長さと、そのなす角度」で決まるということです。
02. 面積を数式の視点で考える
ここから少し代数的に考えてみます。ベクトル \(\mathbf{a}\) と \(\mathbf{b}\) を、次のように座標で表します。
\[
\mathbf{a} = \begin{pmatrix} a_1\\ a_2 \end{pmatrix},
\quad \mathbf{b} = \begin{pmatrix} b_1\\ b_2 \end{pmatrix}
\]
これら2本のベクトルで作られる平行四辺形の面積は、次の式で表すことができます。
\[
S = |a_1 b_2 \,-\, a_2 b_1|
\]
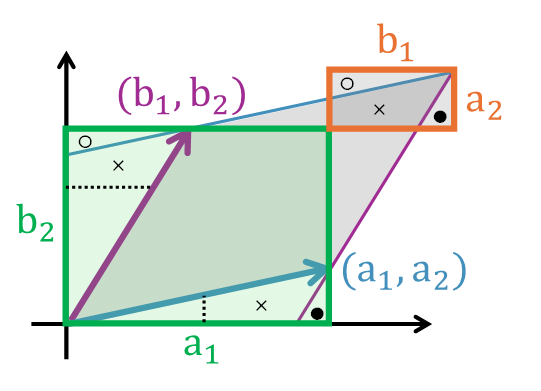
まず「 \(a_1 b_2\) 」で緑色の四角形の面積を計算しています。この緑色の面積は、平行四辺形の面積よりも、「①左上隅(上記の〇の部分)の面積」、「②右下隅(上記の●の部分)の面積」、「③重複部分(上記の×の部分)の面積」の分だけ大きくなっています。
そして、この①②③の面積は「 \(a_2 b_1\) 」で計算される上記オレンジ色の四角形の面積として整理されます。したがって、「 \(a_1 b_2\) 」から「 \(a_2 b_1\) 」を引いてその絶対値をとった先ほどの式が平行四辺形の面積となります。
つまり、緑の部分( \(a_1 b_2\) )には、実際の平行四辺形に含まれないオレンジの部分( \(a_2 b_1\) )が余分に含まれています。そのため、 \(a_1 b_2\) から \(a_2 b_1\) を引いた値が、ちょうど平行四辺形の面積になるのです。
この「 \(a_1 b_2 \,-\, a_2 b_1\) 」という形こそが、まさに行列式の形です。
\[
\det \begin{pmatrix}
a_1 & b_1\\
a_2 & b_2\end{pmatrix}
= a_1 b_2 \,-\, a_2 b_1
\]
つまり、2つのベクトルの座標を並べて作った行列の行列式は、その2本のベクトルで作られる平行四辺形の「面積(の大きさ)」を表しているのです。
03. 行列式の符号の意味
行列式には、面積の大きさだけでなく、「向きの情報」も含まれています。具体的には、行列式が正か負かで「回転の向き」が変わります。
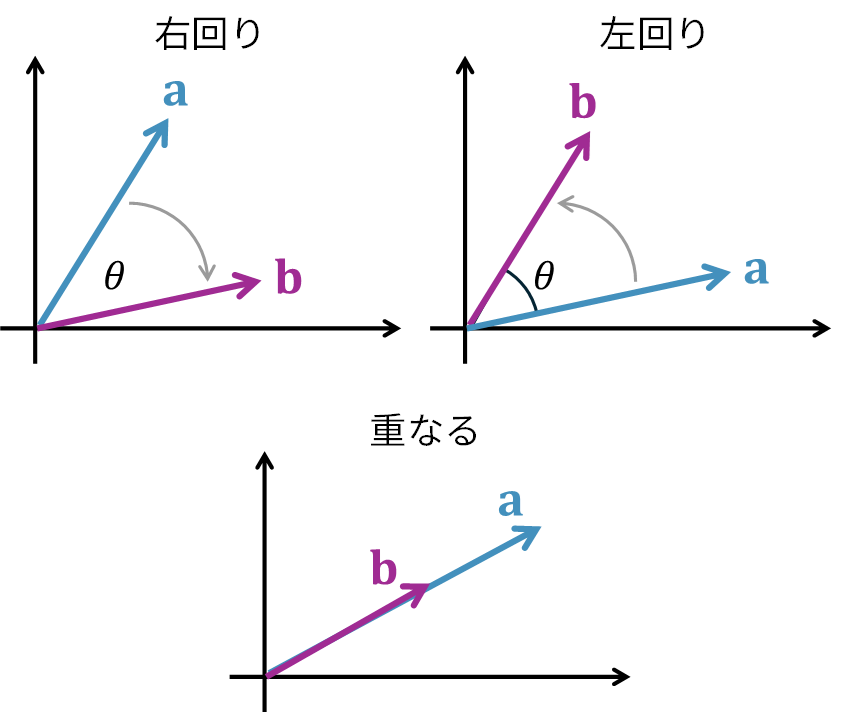
- ベクトル \(\mathbf{a}\) から \(\mathbf{b}\) に右回りに回転するとき → 行列式はプラス
- ベクトル \(\mathbf{a}\) から \(\mathbf{b}\) に左回り(逆方向)に回転するとき → 行列式はマイナス
- 2本のベクトルが重なるとき → 行列式はゼロ
まとめると、次のようになります。
| 位置 | 行列式の値 | 意味 |
|---|---|---|
| 右回り | + | 通常の向き |
| 左回り | − | 反転した向き |
| 2本が重なる | 0 | 面積ゼロ(同一直線上) |
04. 最後に:ヤコビアンへ
ヤコビアンでは、元の \((X, Y)\) 平面の「微小な正方形」が、変換後の \((Z, W)\) 平面でどんな形に変わるのかを調べます。そのとき、元の正方形が「どれだけ広がるか(面積が何倍になるか)」を表すのが、まさにヤコビアンの行列式です。つまり、ヤコビアンの行列式は、元の正方形からの面積の変化率を示しているのです。
行列式は「斜めに掛けて引き算する」というシンプルな計算ですが、その裏には「広がり」と「向き」という、空間の性質を表す深い意味が隠れています。ヤコビアンを理解するうえで、この「行列式=平行四辺形の面積」という感覚を持っておくことが大切です。

