準1級文系解説について(各回共通)
ご訪問いただきありがとうございます。こちらは統計検定🄬準1級合格を目指す方が、公式テキスト『統計学実践ワークブック』やそのほか統計検定🄬準1級対策コンテンツをスラスラと学び進めるために必要な解説を行うブログです。
本ブログは、公開されている「統計検定🄬準1級出題範囲」の各項目について執筆しています。「統計検定🄬準1級出題範囲」は『統計学実践ワークブック』の内容にも対応していますので、本ブログの解説が『統計学実践ワークブック』の読解に役立つ部分も多くあるかと思います。その意味で、本ブログをご覧いただく方には、公式テキスト『統計学実践ワークブック』を購入されることを推奨いたします。
なお、統計検定🄬は一般財団法人統計質保証協会の登録商標です。また、本ブログは一般財団法人統計質保証協会から公認されたコンテンツではありません。
00. はじめに
統計学の根幹を支えるのが「極限定理(limit theorem)」です。データがたくさん集まったとき、確率変数のふるまいはどう近づいていくのか。ここがわかると、標本平均が母平均に近づく理由や、正規分布がなぜ万能なのかも理解しやすくなります。
本記事では、統計検定準1級の出題範囲に沿って、確率変数の「収束」から「中心極限定理」「デルタ法」「極値分布」までを丁寧に整理します。
01. 確率変数の収束
⓪ 確率変数列
「収束」という言葉を理解するためには、まず「確率変数列」というものをイメージしておくことが重要です。
いま、確率変数が1つではなくたくさん並んでいる状態を考えます。
\[ X_{1},X_{2},X_{3},\cdots \]
これを「確率変数列」と呼びます。つまり、 \(X_{n}\) は \(n\) によって中身が変わる「確率変数の“シリーズ”」です。例えば、標本平均を考えてみましょう。
\[ \bar{X}_n=\dfrac{X_1+X_2+\cdots +X_n}{n} \]
これは \(n\) が \(1\) のとき、 \(2\) のとき、 \(3\) のとき…と、 \(n\) が増えるたびに別の確率変数になります。したがって、「標本平均」そのものが実は確率変数列と言えるのです。
\[\begin{align*}
\bar{X}_1 &=\dfrac{X_1}{1}\\[6pt]
\bar{X}_2 &=\dfrac{X_1+X_2}{2}\\[6pt]
\bar{X}_3 &=\dfrac{X_1+X_2+X_3}{3}
\end{align*}\]
ここで、それぞれの \(X_n\) は確率変数で、試行のたびに確率的にさまざまな値をとりえますが、 \(n\) を大きくしていくと、それらの値(例えば上記の標本平均)がある1つの値(母平均 \(\mu\) )に近づいていく性質があります。この「近づき方」の種類を区別したものが、これから見ていく4つの「収束」です。
① 概収束
定義
\[
P\!\left( \lim_{n \to \infty} X_n = X \right) = 1
\]
意味
「ほとんどすべての試行で \(X_n\) が最終的に \(X\) に張りつくように近づく」という、最も強い収束です。
例:コイン投げ

\(X_n\) を「最初の \(n\) 回で表が出た割合」とします。このとき理論的には、 \(n\) を無限に増やすと、 \(X_n\) は表の確率 \(1/2\) にほぼ確実に近づきます。
つまり、ごくまれ(確率としては0)には偏った結果もあるかもしれませんが、現実的には「ほぼ確実に」 \(1/2\) に近づきます。これが「概収束」です。
② 確率収束
定義
\[
\forall \varepsilon > 0,\quad
\lim_{n \to \infty} P(|X_n – X| > \varepsilon) = 0
\]
意味
「どんなに小さな誤差範囲をとっても、標本の大きさ \(n\) を大きくすれば、その誤差を超える確率は限りなく \(0\) に近づく」
例:大数の弱法則
確率収束の定義に、「標本平均 \(\bar{X}_n\) 」と「母平均 \(\mu\) 」を代入すると、まさに大数の弱法則(Law of Large Numbers)が得られます。
\[
\forall \varepsilon > 0,\quad
\lim_{n \to \infty} P(|\bar{X}_n – \mu| > \varepsilon) = 0
\]
つまり、標本平均 \(\bar{X}_n\) は、サンプルサイズを増やすと、母平均 \(\mu\) に確率収束します。これを以下のように表記します。
\[
\bar{X}_n \xrightarrow{p} \mu
\]
③ 平均二乗収束
定義
\[
\lim_{n \to \infty} E[(X_n – X)^2] = 0
\]
意味
「誤差の2乗の平均(MSE)が0に近づく」、つまり、「誤差の平均的な大きさが消えていく」ということです。
大数の弱法則との関係
平均二乗収束する確率変数列は確率収束も満たします。確率収束の例として紹介した大数の弱法則についても、標本平均 \( \bar{X}_n\) が母平均 \(\mu\) に平均二乗収束することから導かれるものです。
\[
\lim_{n \to \infty} E[(\bar{X}_n – \mu)^2] = 0
\]
④ 分布収束
定義
確率変数列 \(\{X_n\}\) が確率変数 \(X\) に分布収束するとき、以下のように定義されます。
\[
\lim_{n \to \infty} F_{X_n}(x) = F_X(x)\\[6pt]
(\text{ただし $x$ は $F_X(x)$ の連続点※})
\]
ここで、 \(F_{X_n}(x)\) は \(X_{n}\) の分布関数を表し、 \(F_{X}(x)\) は収束先の分布関数(極限分布)を表しています。また、関数 \(F\) は連続な関数とします。
なお、分布関数 \(F_{X_n}(x)\) とは、 \(X_{n}\) が \(x\) 以下の値をとる確率を示す関数で、すなわち、 \(F_{X_n}(x)=P(X_{n} \le x)\) です。
意味
「確率分布の形そのものが近づく」、つまり、「値が近づくとは限らないものの、分布関数の形が同じになる」ということです。
例:中心極限定理
母集団からの独立同分布( \(i.i.d.\) )の標本 \(X_1, X_2, \dots, X_n\) を考えます。それぞれの平均と分散を
\[E[X_i] = \mu, \quad V[X_i] = \sigma^2 \\ (\text{ただし } 0 < \sigma^2 < \infty)\]
と仮定します。このとき、標準化された標本平均
\[Z_n = \frac{\sqrt{n}(\bar{X}_n – \mu)}{\sigma}\]
の分布は、標本の大きさ \(n\) を増やすと標準正規分布 \(N(0,1)\) に近づいていきます。これを「中心極限定理」と呼びます。
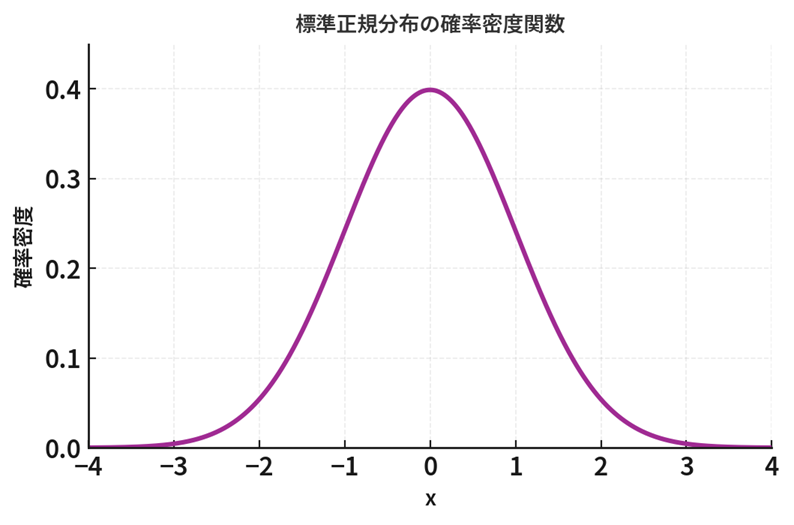
分布収束と中心極限定理
中心極限定理を分布収束の定義
\[
\lim_{n \to \infty} F_{X_n}(x) = F_X(x)
\]
に対応させると以下のように整理できます。
| 一般の記号 | 中心極限定理での対応 | 意味 |
|---|---|---|
| \(X_n\) | \(Z_n = \dfrac{\sqrt{n}(\bar{X}_n – \mu)}{\sigma}\) | 標準化された標本平均 |
| \(X\) | \(Z \sim N(0,1)\) | 標準正規分布に従う確率変数 |
| \(F_{X_n}(x)\) | 標本平均の標準化 \(Z_n\) の分布関数 | サンプルサイズ \(n\) における実際の分布 |
| \(F_X(x)\) | 標準正規分布の分布関数 \(\Phi(x)\) | 極限での理想的な分布 |
上記を踏まえ数式に整理すると以下のように表記できます。なお、「 \((\forall x \in \mathbb{R})\) 」は「for all Real numbers \(x\) 」、つまり、「すべての実数 \(x\) について」ということを意味しています。
\[\begin{align*}
\lim_{n \to \infty} F_{Z_n}(x)
&= \lim_{n \to \infty} P(Z_n \le x)\\[6pt]
&= \Phi(x)\quad (\forall x \in \mathbb{R})
\end{align*}\]
ここで、 \(\Phi(x)\) は標準正規分布 \(N(0,1)\) の分布関数を表します。
\[
\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-t^2 / 2} \, dt
\]
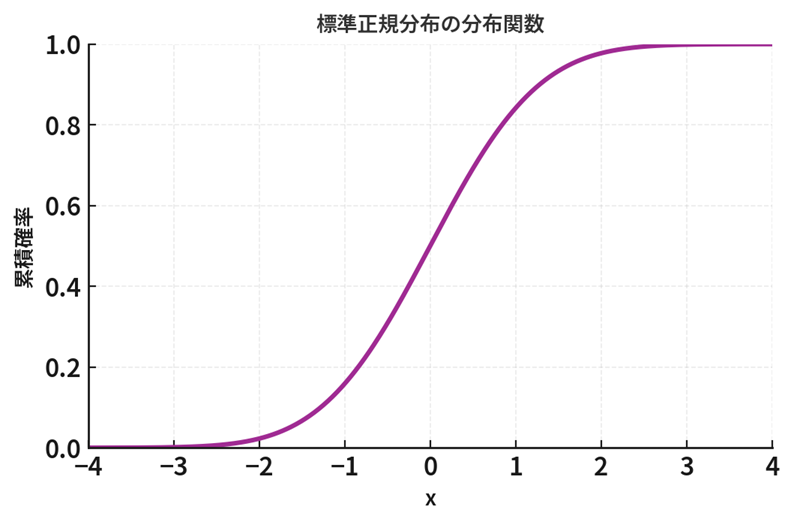
上記の中心極限定理の内容を言葉でまとめておくと
「標準化された標本平均 \(Z_n\) の分布関数 \(F_{Z_n}(x)\) は、 \(n\) を大きくすればするほど、標準正規分布の分布関数 \(\Phi(x)\) に限りなく近づく」
ということになります。
02. 極値分布
これまでは「平均がどう収束するか」を見てきましたが、今度は視点を変えて「一番大きい(あるいは小さい)値」に注目します。例えば「1年間の最高気温」や「100人中で一番高い身長」といった“極端な値”の分布を扱うのが極値分布です。
最大値の確率とは?
独立な確率変数 \(X_1, X_2, \dots, X_n\) があるとき、最大値を以下のように書きます。
\[
M_n = \max(X_1, X_2, \dots, X_n)
\]
この最大値 \(M_{n}\) がある値 \(x\) 以下となる確率 \(P(M_{n} \le x)\) は、「全員が \(x\) 以下である確率」と言い換えることができます。そして、「全員が \(x\) 以下である確率」は「それぞれの確率変数が \(x\) 以下である確率(分布関数)」の積として、以下のように表せます。
\[\begin{align*}
P(M_n \le x) &=\prod_{i=1}^n P(X_i\le x)\\[5pt]
&= \bigl[ P(X_{i} \le x) \bigr] ^n = \bigl[ F(x) \bigr] ^n
\end{align*}\]
ここで \(F(x)\) は各 \(X_i\) の分布関数です。互いに独立で、かつ、同じ分布にしたがうため、すべての \(X_i\) について同一の \(F{x}\) が使えます。
位置とスケールの調整
サンプルが増えると、 \(M_n\) はどんどん大きくなってしまい、そのままだと極限が \(\infty\) になってしまいます。そこで、位置とスケールを調整することを考えます。
\[
Y_{n}=\dfrac{M_{n}-b_{n}}{a_{n}}
\]
このとき、調整のための \(b_{n}\) や \(a_{n}\) をうまく選ぶと、調整後の \(Y_n\) は特定の分布に分布収束します。このときの分布が極値分布です。
3つの代表的な分布
位置とスケールの調整による収束先は、以下の3つの分布型となります。
| 収束先分布 | 分布関数の形状 | 代表的な元の分布 | 分布関数 |
|---|---|---|---|
| ガンベル分布 | S字カーブ (単調増加の滑らかな曲線) | 正規・指数・幾何分布など (裾が指数的に減少) | \(G(x)=\exp(-e^{-x})\) |
| フレシェ分布 | 右にゆっくり上がる | パレート分布など (裾が重い) | \(G(x)=\exp(-x^{-\alpha})\ (x>0)\) |
| ワイブル分布 | 右側(0)で打ち止め | 一様分布など (上限がある) | \(G(x)=\exp(-(-x)^{\alpha})\ (x< 0)\) |
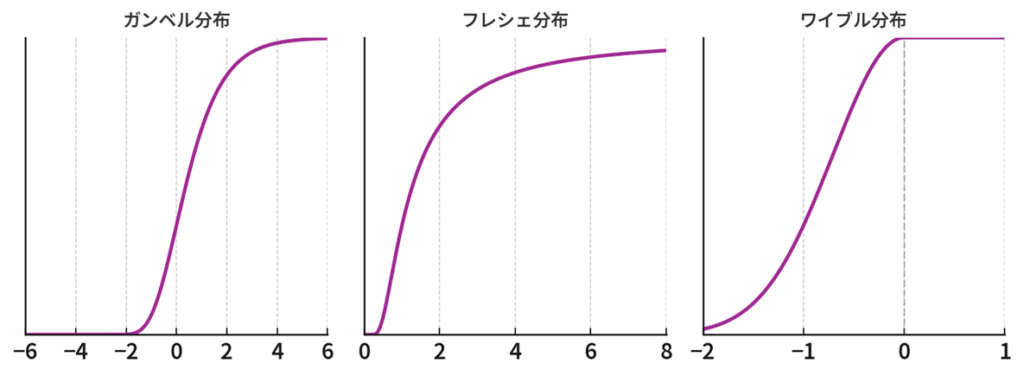
例:指数分布
ここでは、最大値がどのようにガンベル分布に近づくかを、具体的に見てみましょう。確率変数 \(X_1, X_2, \dots, X_n\) が互いに独立に平均1の指数分布に従う( \(i.i.d.\) )ものとします。このとき、指数分布の分布関数は以下のように与えられます。
\[
F(x) =
\begin{cases}
0 & (x < 0)\\[6pt]
1 – e^{-x} & (x \ge 0)
\end{cases}
\]
したがって、最大値 \(M_n = \max(X_1, \dots, X_n)\) の分布関数は( \(i.i.d.\) の仮定より)
\[
P(M_n \le x) = [F(x)]^n = (1 – e^{-x})^n \quad (x \ge 0)
\]
と書けます。ここで、次のように置き換えます。
\[
x = y + \log n
\]
これは「自然対数の底 \(e\) 」の性質を利用して、式の中に現れる \(n\) と指数 \(e^{-x}\) をきれいに整理するための置き換えです。実際、この置き換えを使うと( \(e^{-\log n}=n^{-1}\) であることに注意して)
\[\begin{align*}
P(M_n \le y + \log n )
&= \left(1 – e^{-(y + \log n)}\right)^n\\[6pt]
P(M_n – \log n \le y) &= \left(1 \, – \; e^{-y} \cdot e^{-\log n}\right)^n\\[6pt]
P(M_n – \log n \le y) &= \left(1 \, + \, \frac{-e^{-y}}{n}\right)^n
\end{align*}\]
と整理できます。ここで、自然対数の底 \(e\) の性質
\[
\lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n = e^{x}
\]
を思い出すと、これと同じ形が現れていることがわかります。この極限を使えば、
\[
\left(1 \, + \, \frac{-e^{-y}}{n}\right)^n \to e^{-e^{-y}}
\]
が得られます。この関数 \(e^{-e^{-y}}\) は、ガンベル分布の分布関数そのものです。したがって、
\[
M_n – \log n \xrightarrow{d} \text{ガンベル分布}
\]
と結論づけられます。つまり、最大値 \(M_{n}\) の位置を \(\log n\) だけずらすと、ガンベル分布に近づくということです。
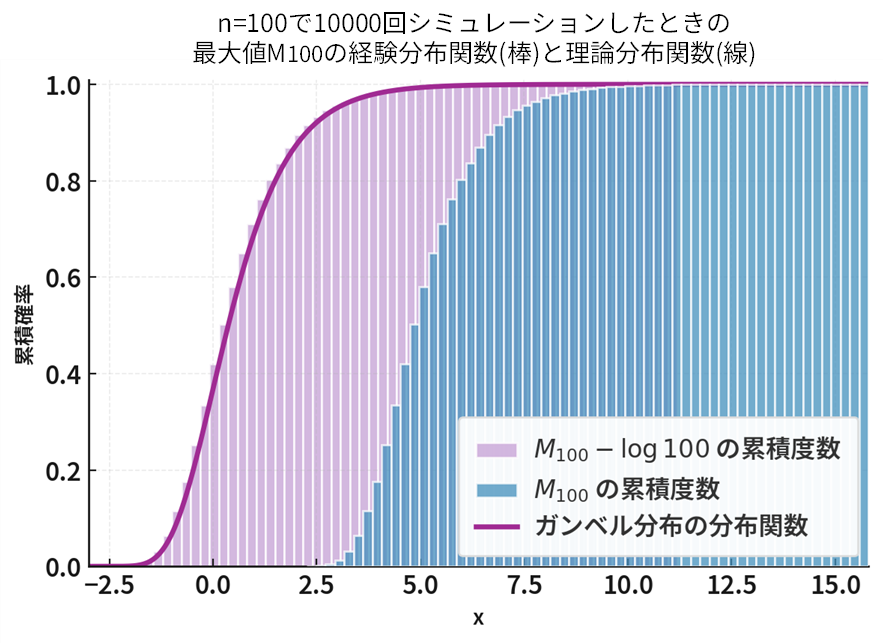
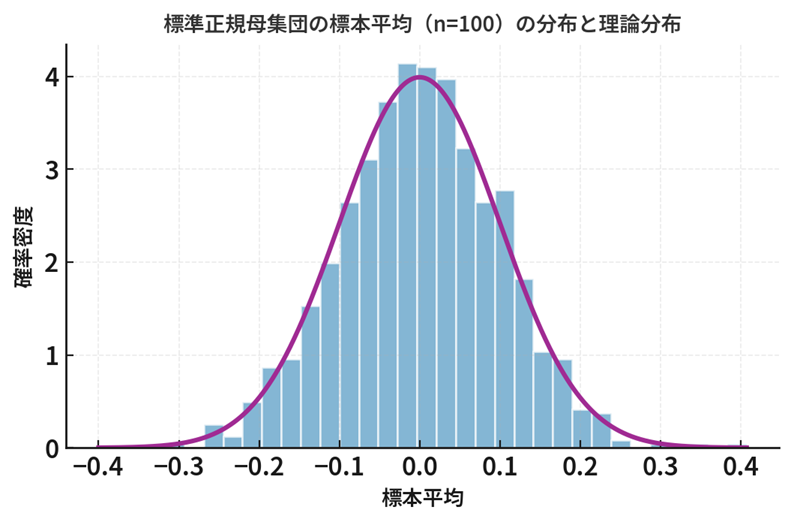
上記の図は、平均 \(1\) の指数分布から独立に抽出した標本サイズ \(n=100\) の最大値 \(M_{100}\) を、 \(10,000\) 回シミュレーションして得た結果です。濃い青は \(M_{100}\) の累積度数分布(積み上げヒストグラム)、薄紫は \(M_{100}-\log 100\) の累積度数分布です。位置調整( \(-\log n\) )により分布全体が左へ平行移動し、理論上のガンベル分布の分布関数(紫の曲線)に重なっていく様子が確認できます。これは「指数分布の最大値について \(M_n-\log n\) がガンベル分布に収束する」を可視化したものです。
03. 連続写像定理とスルツキーの補題
ここでは分布収束における2つの重要な性質についてみていきましょう。統計検定®2級レベルの段階ではあまり気にすることがなかったかもしれませんが、これらの性質のおかげで分布の変換をスムーズに行うことができます。
連続写像定理
以下のように分布収束が成り立っているものとします。
\[
X_n \xrightarrow{d} X
\]
このとき、 \(f\) が連続な関数なら以下の収束が成り立ちます。これを連続写像定理と呼びます。
\[
f(X_n) \xrightarrow{d} f(X)
\]
つまり、分布収束が成り立つとき、元の確率変数を関数に投入して変換しても、収束は崩れないということです。
例:正規分布からカイ二乗分布
中心極限定理から以下の分布収束が成り立ちます。
\[
\frac{\sqrt{n}(\bar{X}_n – \mu)}{\sigma} \xrightarrow{d} N(0,1)
\]
ここで左辺、右辺のいずれにも連続な関数 \(f(z)=z^2\) を適用(埋め込むイメージです)すると
\[
\left( \frac{\sqrt{n}(\bar{X}_n – \mu)}{\sigma} \right)^2 \xrightarrow{d} \chi^2{(1)}
\]
となります。標準正規分布にしたがう確率変数を2乗するとカイ二乗分布にしたがう…とは2級試験の段階で学びますが、この関係をより一般的かつ力強く支えているのが、この連続写像定理という理論です。
スルツキーの補題
以下のように分布収束および確率収束が成り立つとします。なお、 \(c\) は任意の定数とします。
\[
X_{n} \xrightarrow{d} X, \;\; Y_{n} \xrightarrow{p} c
\]
このとき、次の分布収束が成り立ちます。これをスルツキーの補題と呼びます。
\[\begin{align*}
X_{n}+Y_{n} &\xrightarrow{d} X+c\\[6pt]
X_{n} Y_{n} &\xrightarrow{d} cX\\[9pt]
\dfrac{X_{n}}{Y_{n}} &\xrightarrow{d} \dfrac{X}{c} \quad (c \neq 0)
\end{align*}\]
これは、「確率的に定数に近づく変数」が混ざっても、それはほとんど定数として扱ってよい、というルールです。
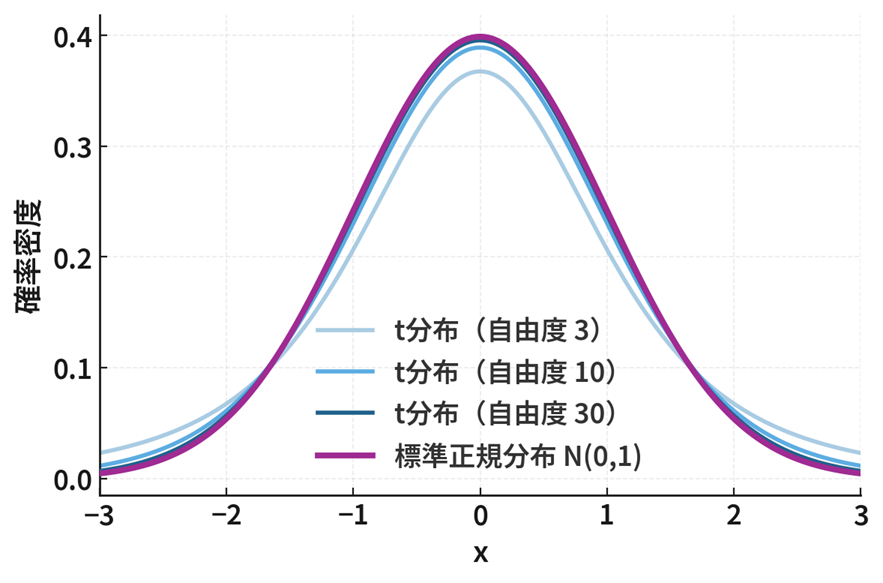
例:\(t\) 分布から標準正規分布
\(t\) 分布は、「標本平均のズレ」を「標本のばらつき」で割った統計量として定義されます。一般的には、自由度 \(n-1\) の \(t\) 分布にしたがう確率変数は次の式で表されます。
\[
T_{n}=\dfrac{\sqrt{n}(\bar{X}_{n} – \mu)}{S_{n}}
\]
なお、それぞれの記号が表すものは以下の通りです。
- \(\bar{X}_{n}\) :標本平均
- \(\mu\) :母平均(定数)
- \(S_{n}\) :標本標準偏差(確率変数)
このとき、分母の標本標準偏差 \(S_{n}\) が母標準偏差 \(\sigma\) に確率収束すると仮定すると(証明は割愛しますが実際に確率収束します)、スルツキーの補題より
\[
T_{n}=\dfrac{\sqrt{n}(\bar{X}_{n} – \mu)}{S_{n}} \xrightarrow{d}
\dfrac{\sqrt{n}(\bar{X}_{n} – \mu)}{\sigma}
\]
となります。ここで、右辺の確率変数は中心極限定理により標準正規分布 \(N(0,1)\) にしたがうため、以下のようにまとめられます。
\[
T_{n}=\dfrac{\sqrt{n}(\bar{X}_{n} – \mu)}{S_{n}} \xrightarrow{d} N(0,1)
\]
つまり、自由度 \(n-1\) の \(t\) 分布は、極限をとると( \(n\to\infty\) )標準正規分布に収束することを意味します。
04. モーメント母関数と分布収束
確率分布の収束を調べるとき、実はもう一つ、より「なめらかに」収束をとらえる方法があります。それが「分布を母関数として見る」考え方です。
分布をモーメント母関数で表す(復習)
確率変数 \(X\) が与えられたとき、その分布の特徴をすべて含んだ関数として、次のようなものを定義します。
\[
M_X(\theta) = E[e^{\theta X}]
\]
これを モーメント母関数(Moment Generating Function:MGF) と呼びました。\(\theta\) (シータ)は「分布の形を探るためのパラメータ」です。

モーメント母関数のイメージ(復習)
モーメント母関数は、その名の通り「モーメント(=平均・分散・歪度など)」の生成に利用できる関数です。実際、 \(\theta\) で微分して \(\theta =0\) を代入すれば、平均・分散を取り出せます。
\[
M_X'(0) = E[X], \quad M_X^{\prime\prime}(0) = E[X^2]
\]
つまり、 \(M_X(\theta)\) を知っていれば、その分布の「かたち」や「広がり」をうまく復元できるのです。モーメント母関数は、分布のいわば「設計図」のような存在です。

分布収束とモーメント母関数の収束
確率変数列 \(X_n\) のモーメント母関数が \(X\) のモーメント母関数に収束するとき、 \(X_{n}\) は \(X\) に分布収束します。ただし、 \(M_{X}(\theta)\) が \(\theta=0\) の近傍で有限に定義されるものとします。
\[\begin{align*}
M_{X_n}(\theta) &\to M_X(\theta) \quad (\theta\ \text{が0の近傍で})\\[6pt]
\Rightarrow \quad X_n &\xrightarrow{d} X
\end{align*}\]
つまり、分布の「設計図」であるモーメント母関数が \(\theta=0\) の周りで同じ形に近づけば、その分布自体も近づくと考えてよい、ということです。モーメント母関数は平均・分散などのモーメント情報をすべて内包しているため、その関数が滑らかに一致していくなら分布も滑らかに一致していく、と理解しておくとよいでしょう。
この方法のよいところは、積分や畳み込みといった煩雑な計算を扱わずに、「関数の極限」という観点から分布の収束を論じられる点にあります。
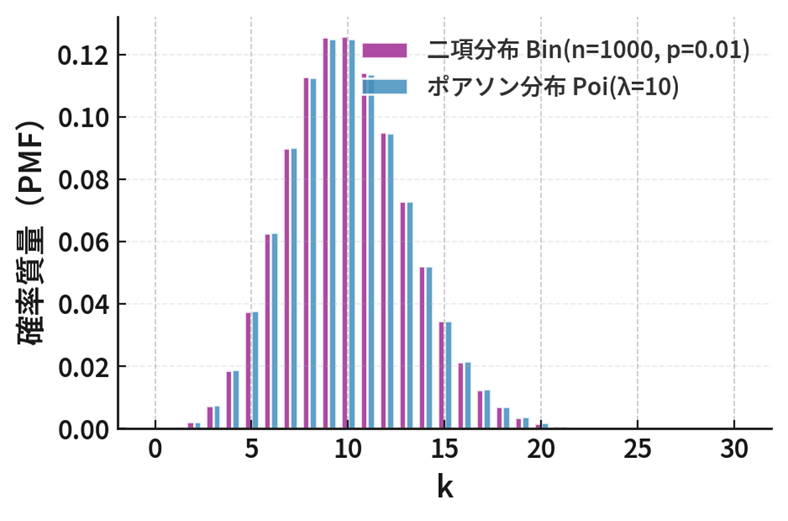
例:二項分布からポアソン分布
モーメント母関数を使うと、例えばよく知られた「二項分布がポアソン分布に近づく」という関係も簡単に示すことができます。
(1) 二項分布のモーメント母関数
二項分布 \(B(n,p)\) の確率変数 \(X\) のモーメント母関数は以下の通りです。
\[
M_X(\theta) = (1 – p + pe^{\theta})^n
\]
導出については第2回の記事でもご紹介していますので、復習されたい方は以下もご覧ください。

(2) パラメータの極限を設定
「試行回数 \(n\) が大きく、成功確率 \(p\) が小さい」場合、平均 \(np\) を一定値 \(\lambda\) に保つように \(p = \lambda / n\) とおきます。
\[\begin{align*}
M_X(\theta) &= \left(1 \, – \dfrac{\lambda}{n} + \dfrac{\lambda}{n} e^{\theta}\right)^n\\[8pt]
&= \left(1 \, + \dfrac{-\lambda(1 – e^{\theta})}{n}\right)^n
\end{align*}\]
(3) \(n\to\infty\) の極限をとる
ここで、自然対数の底 \(e\) の定義
\[
\lim_{n\to\infty}\left(1 + \frac{x}{n}\right)^n = e^x
\]
を使うと、
\[
\lim_{n\to\infty} M_X(\theta) = e^{-\lambda(1 – e^{\theta})}
\]
右辺の式が、実は、パラメータ \(\lambda\) のポアソン分布のモーメント母関数と一致します(導出は「離散型確率分布」についての記事でご紹介したいと思います)。したがって、以下の分布収束が成り立ちます。
\[
X_n \xrightarrow{d} Y \quad (Y \sim \mathrm{Poisson}(\lambda))
\]
これが「少数法則」(まれな出来事が一定の平均回数で起こる)の数式的な裏づけです。
05. デルタ法
デルタ法の基本
デルタ法は、「推定量を関数 \(f\) に投入して変換したら、その分布はどう変わるのか?」を考えるときに使う道具です。例えば、標本平均のような推定量 \(\hat{\theta}_n\) が母数 \(\theta\) に確率収束し、さらに中心極限定理により以下の分布収束が成立しているとします。
\[
\sqrt{n}(\hat{\theta}_n – \theta) \xrightarrow{d} N(0, \sigma^2)
\]
このとき、 \(\hat{\theta}_n\) を関数 \(f\) に投入した \(f(\hat{\theta}_n)\) の分布がどのように変わるかを求める方法がデルタ法です。
デルタ法の前提
ここで重要なのは、関数 \(f\) が「 \(\theta\) のまわりでなめらか」であることです。つまり、「 \(\theta\) の近くで、 \(f\) がとがったり折れ曲がったりせず、ゆるやかに変化する関数である必要があります。これは数学的には、 \(f\) が微分可能(=テイラー展開ができる)ことを意味します。
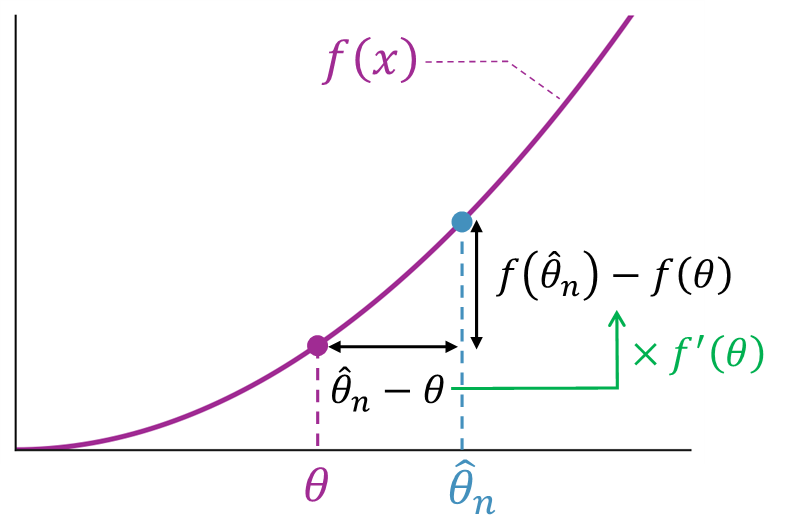
具体的には、テイラー展開を用いることで次のような近似式を導くことができます(ここでは、 \(\hat{\theta}_n\) と \(\theta\) の差が十分に小さいものとします)。
\[\begin{align*}
f(\hat{\theta}_n) &\approx f(\theta) + f'(\theta)(\hat{\theta}_n – \theta)\\[6pt]
\Rightarrow
f(\hat{\theta}_n) \, – f(\theta) &\approx f'(\theta)(\hat{\theta}_n – \theta)
\end{align*}\]
この式は、「関数 \(f\) の変化(上記2行目の左辺)」が \(f'(\theta)\) (上記2行目の右辺の係数)で表されることを意味しています。つまり、推定量のズレ \(\hat{\theta}_n – \theta\) の \(f'(\theta)\) 倍だけ関数 \(f\) が変化するということです。
デルタ法の数式
上記を踏まえると、次のようにまとめられます。
\[\begin{align*}
\sqrt{n}(\hat{\theta}_n – \theta) &\xrightarrow{d} N(0, \sigma^2)\\[6pt]
\Rightarrow
\sqrt{n}\big(f(\hat{\theta}_n) – f(\theta)\big) &\xrightarrow{d} N\!\big(0, [f'(\theta)]^2 \sigma^2\big)
\end{align*}\]
これはつまり、「もとの分散 \(\sigma^2\) が、投入した関数の変化率(導関数 \(f'(\theta)\) )の二乗だけ拡大・縮小(スケール)される」ということです。
例:標本平均の平方
標本平均 \(\bar{X}_n\) が母平均 \(\mu\) に対して以下の分布収束を満たしているとします。
\[
\sqrt{n}(\bar{X}_n – \mu) \xrightarrow{d} N(0, \sigma^2)
\]
ここで、標本平均 \(\bar{X}_n\) を関数 \(f(x) = x^2\) に投入して変換する場合を考えます。このとき導関数は \(f'(\mu) = 2\mu\) なので、デルタ法を用いて以下のように整理できます。
\[
\sqrt{n}\big(\bar{X}_n^2 – \mu^2\big) \xrightarrow{d} N(0, (2\mu)^2\sigma^2)
\]
このことから、( \(\mu \neq 0\) のとき)平方にすることで分散が \((2\mu)^2\) 倍にスケールされたことがわかります。
06. まとめ
極限定理や収束の考え方は、一見むずかしく感じるかもしれませんが、要するに「データが増えたとき、どんなふうに落ち着いていくのか」を見ているだけです。
標本平均が母平均に近づく、大数の法則で安定していく、そして確率分布そのものが正規分布などの“かたち”に近づいていく…といったことが極限の視点でつながっているのです。
数学的な式の背後には、確率という「ゆらぎ」がありますが、そこに秩序(例えば「収束」)を見出そうとするのが統計学の面白さです。少しずつで構いませんので、数式の意味をかみしめながら、自分のペースで読み進めていきましょう。

