目次
2. 確率統計
(1) 事象と確率
試行によって起こる個々の結果の集合を事象（event）と呼び、すべての結果を含んだ集合を全事象（Ω）と呼びます。
- 和事象：複数の事象のうち少なくとも1つが起こる事象
- 積事象：複数の事象が同時に起こる事象
- 空事象：何も起こらないという事象
- 排反：任意の2つの事象が同時に起こらない（＝積事象が空事象）
和事象の確率は各事象の確率の和から積事象を引いて計算されます。
(2) 条件付き確率
条件付き確率は「事象Aが起こるという条件下で事象Bが起こる確率」、具体的には以下の式で計算できます。
条件付き確率の式を「P(A∩B)＝…」と変形したものが乗法定理です。
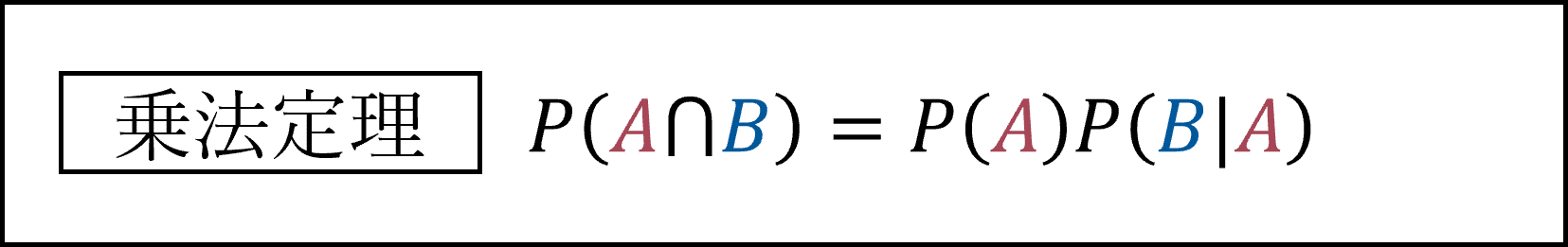
事象Aが起こるか否かがもう事象Bの起こる確率に影響しないとき「事象Aと事象Bは独立である」と言います。このとき確率についての以下の式が成り立ちます。
(3) ベイズの定理
ベイズの定理は「事象A」が起こる原因として「事象B1,B2,…,Bn」が考えられるとき、「事象Aが起きたときにその原因が(B1,B2,…,Bnのうちの)B1である確率」が分かるもので、これは以下の式により計算されます。
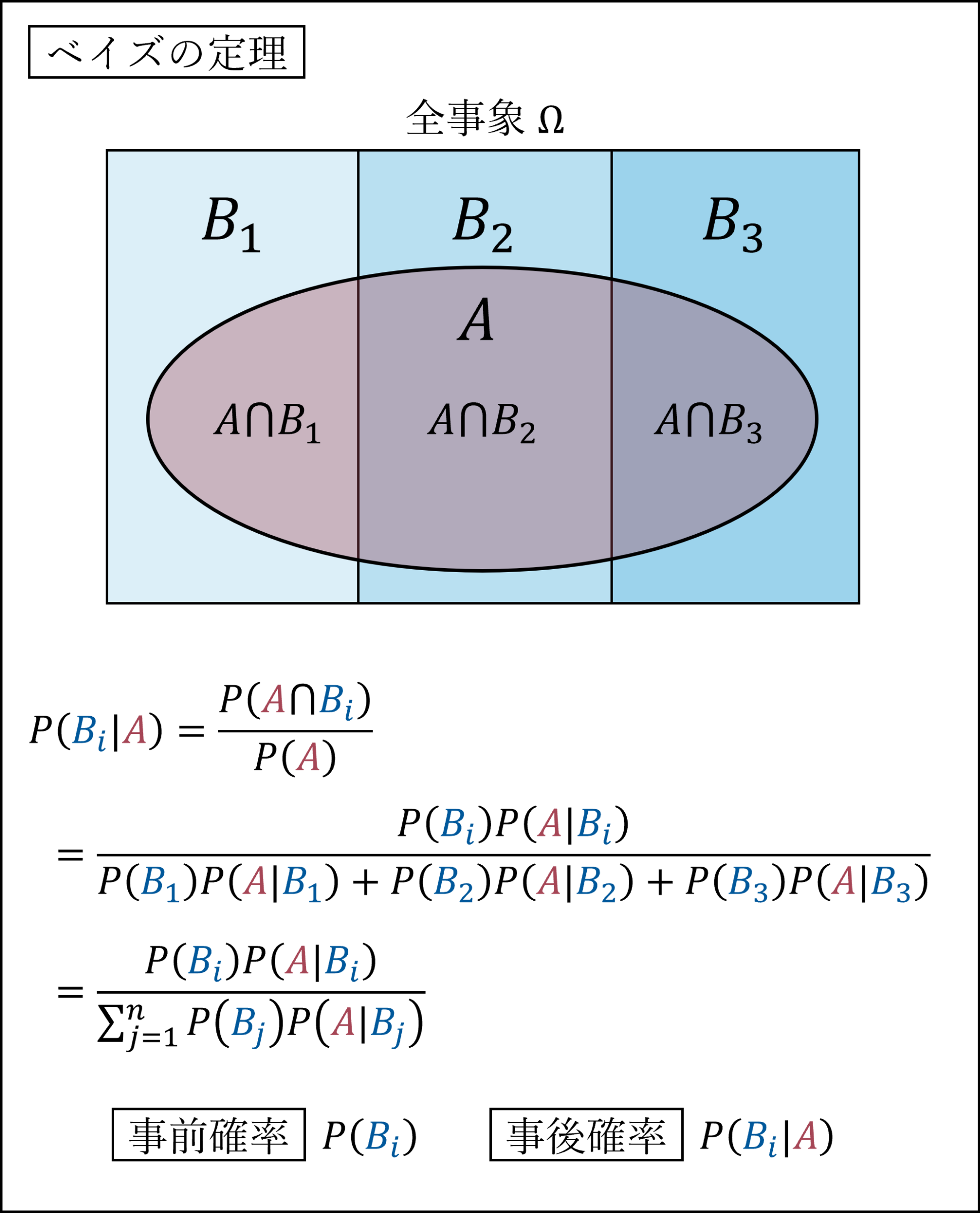
- 事前確率：原因事象Bi（i＝1,2,…,n）の確率
- 事後確率：事象Aが起きたときに事象Bi（i＝1,2,…,n）が起こっている確率（事象Aが起きたときにその原因が事象Biである確率）
例題を用意しました↓
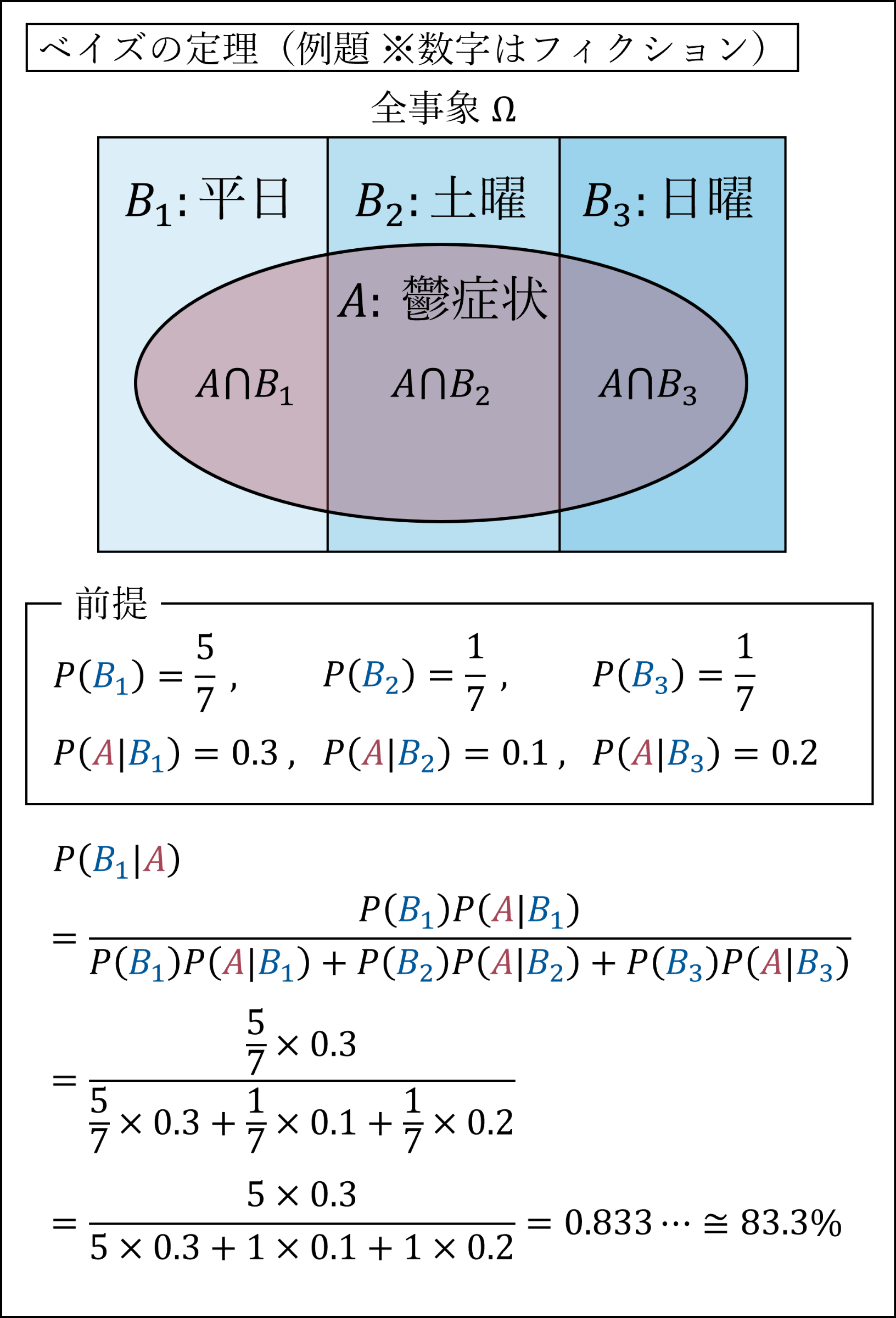
上記のベン図および確率の前提のもとでは「鬱症状が起きたときに平日である確率＝83.3%」であると計算されています。
これは、
- 【事前】今日が平日である確率＝5/7＝71.4%
- 【事後】今日が平日である確率＝83.3%
というように、確率が更新されたという見方ができます。
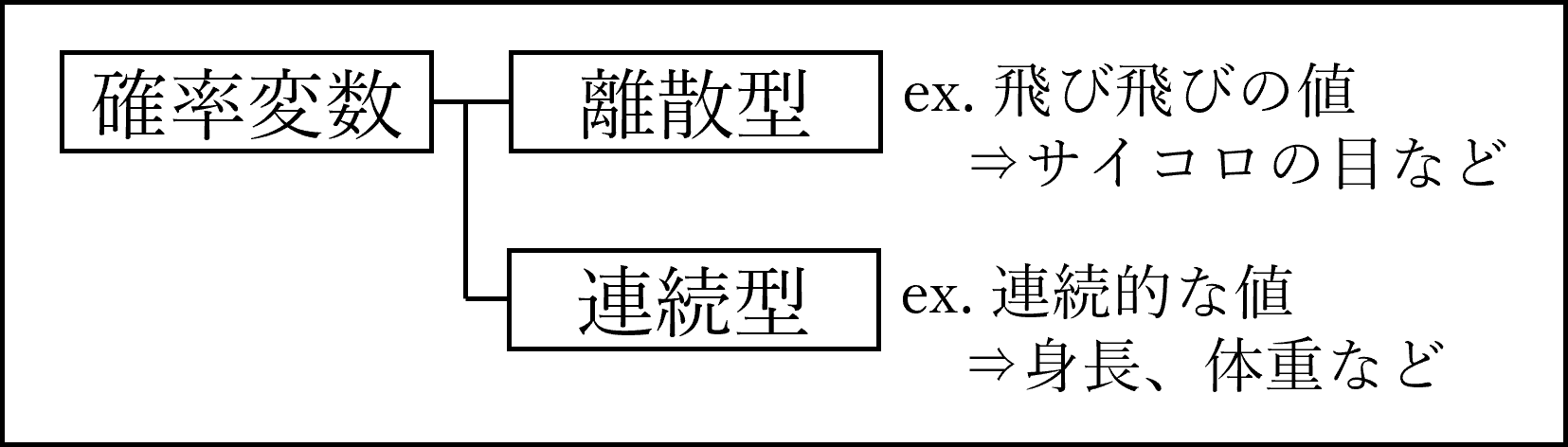
(4) 確率変数と確率分布
とりうる値に対して確率が付与される変数を確率変数と呼び、変数の値が離散的（飛び飛び）な値をとる場合を離散型確率変数、連続的な値（間に無数の値が存在するような値）をとる場合を連続型確率変数と呼びます。
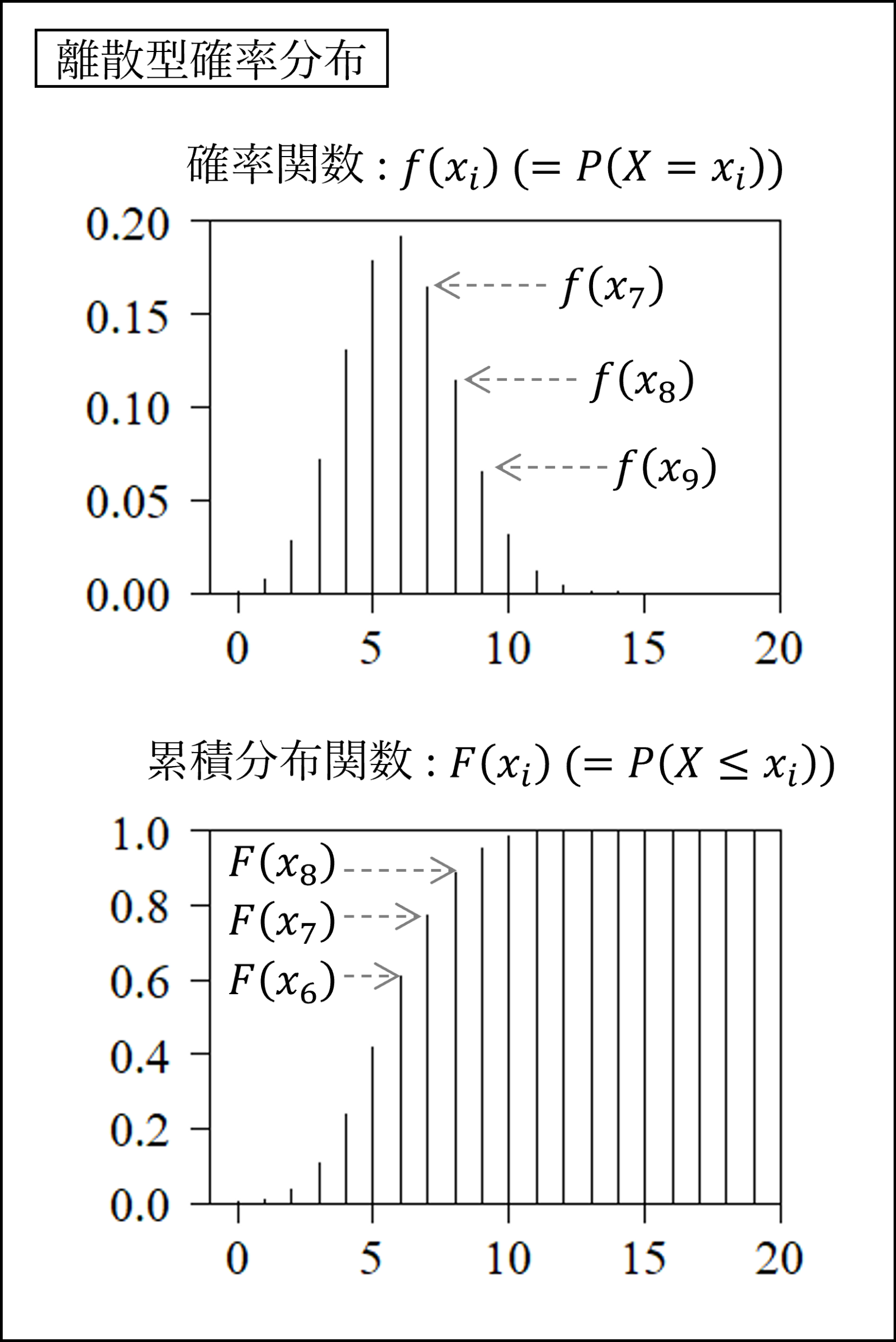
離散型確率分布は横軸に確率変数を、縦軸に確率をとって図示されます。離散型確率分布の場合は値が離散的ですので確率の大きさが棒線で示されます。
なお、確率の大きさ（図の棒線の長さ）は確率関数という確率のルールを表現する式によって計算され、値の小さい側から確率を累積させたものが下段の累積分布と呼ばれるものになります。
連続型確率分布は横軸に確率変数を、縦軸に確率密度をとって図示されます。連続型確率分布の場合は値が連続的ですので確率の大きさが面積（黒線の下側の面積）で示されます。
なお、確率密度の大きさ（図の黒線の高さ）は確率密度関数という式によって計算されます。また、値の小さい側から確率（面積）を累積させたものが下段の累積分布と呼ばれるものになります
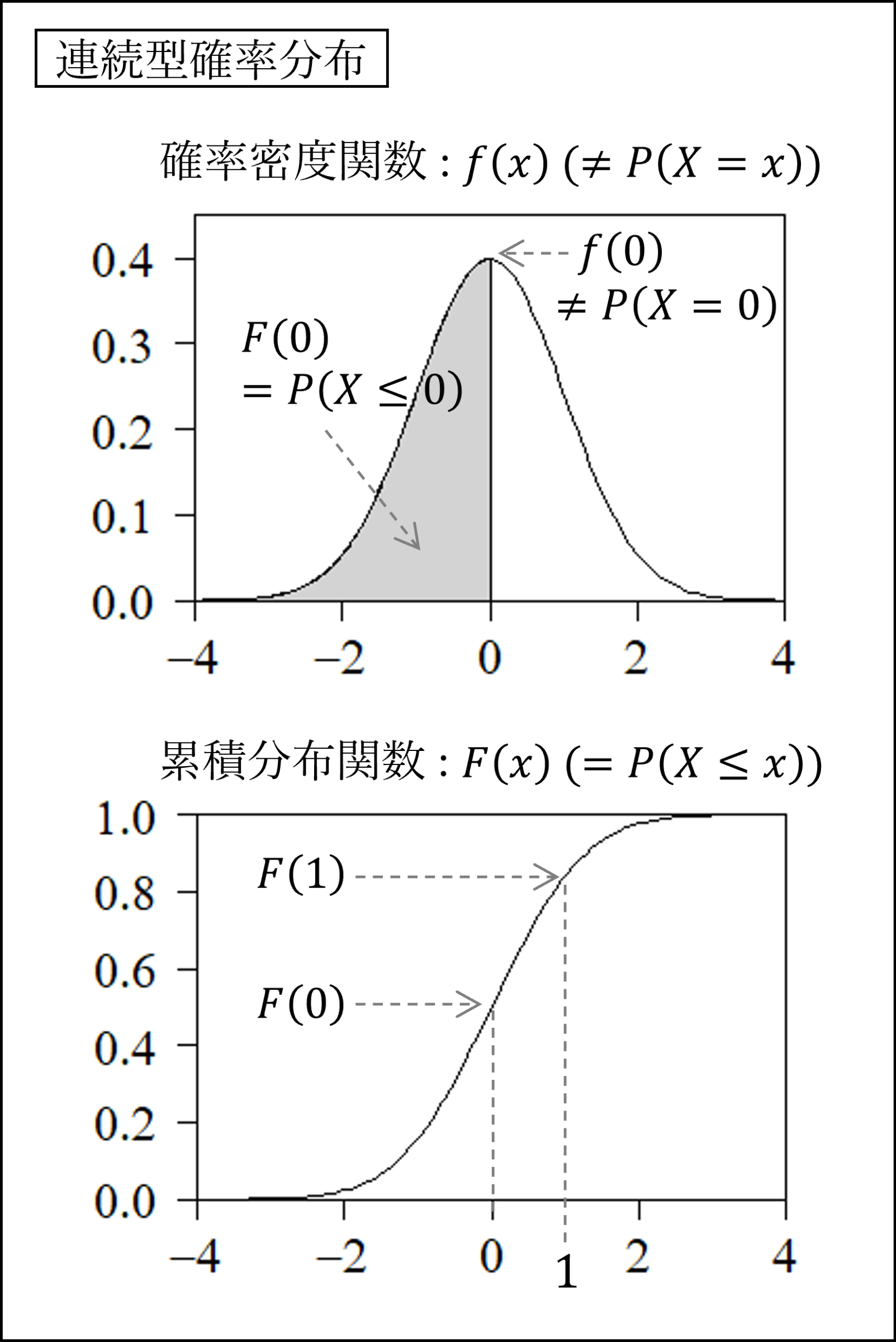
上記の図においては横軸の確率変数が0以下となる確率P(X≤0)が、上図では灰色部分の面積で示され、下図では横軸がX＝0となるときの黒線の高さで示されています。
(5) 期待値と分散
確率変数の期待値は、確率変数が「どのような値になると期待されるか」を表し、分布の重心を意味します。
また、確率変数の分散は、確率変数の「母平均μからの偏差の2乗がどのような値になると期待されるか」を表し、分布のばらつきの程度を表します。
具体的には以下の式によって計算されます。
例題を用意しておきました↓
期待値は「各値を確率で重み付けしたもの」ということが上記の期待値の計算からもわかるかと思います。
上記は離散型確率変数についてでしたが、連続型確率変数の場合も考え方は同様です（連続型の場合は確率を面積で考える必要がありますので積分という方法により計算されます）。
こちらも例題を用意しました↓
期待値と分散については以下の公式を覚えておきましょう。
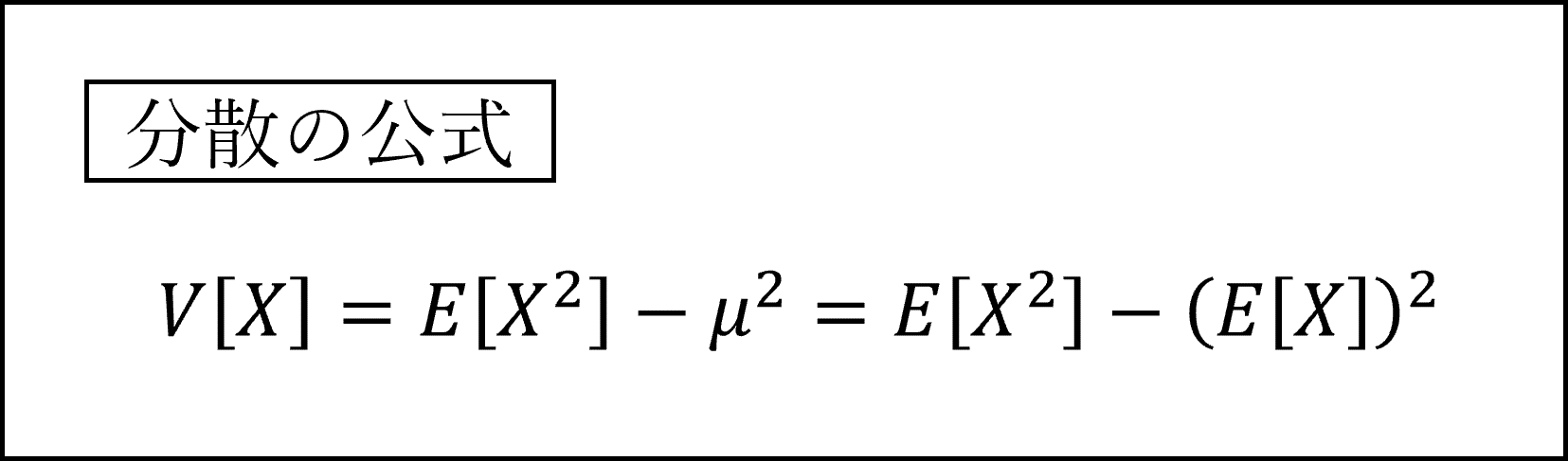
なお、確率変数Xの1次式（変数Xが2乗,3乗,…されていない式）の期待値と分散は以下のように計算されます。
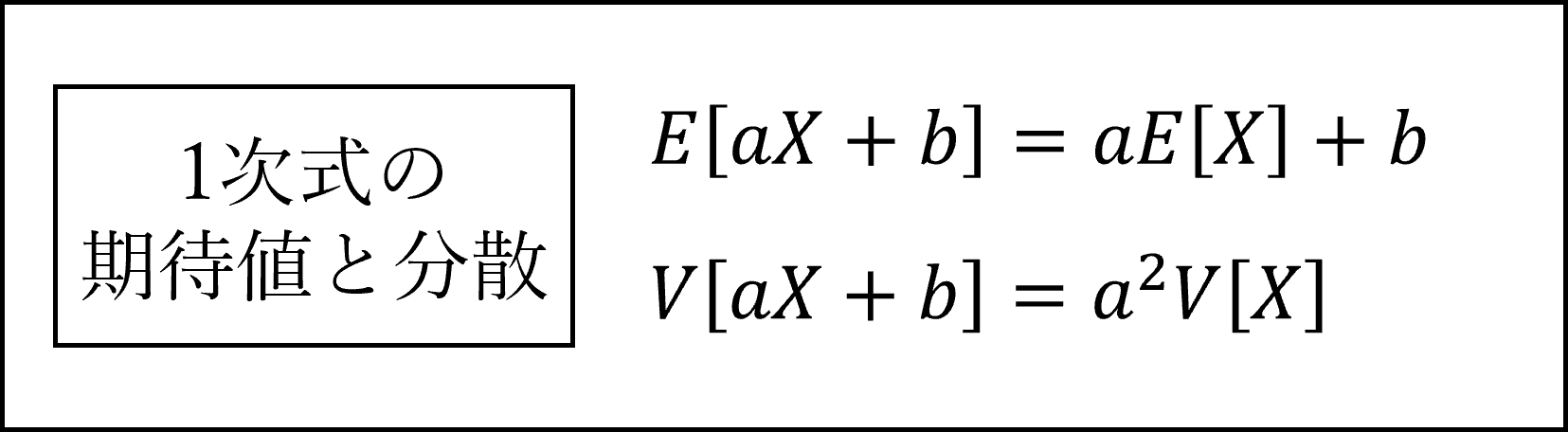
(6) 離散型確率分布
ここからは主な離散型確率分布を紹介していきます。
まずはベルヌーイ分布です。成功確率pの試行結果（例：コイン投げで表が出る、サイコロの目が偶数、くじ引きで当たりを引く…）がしたがう分布になります。
次に二項分布です。成功確率pの試行をn回行ったときの成功回数（例：0.2の確率でアタリとなるくじ引きを10回引いたときのアタリの回数…）がしたがう分布になります。
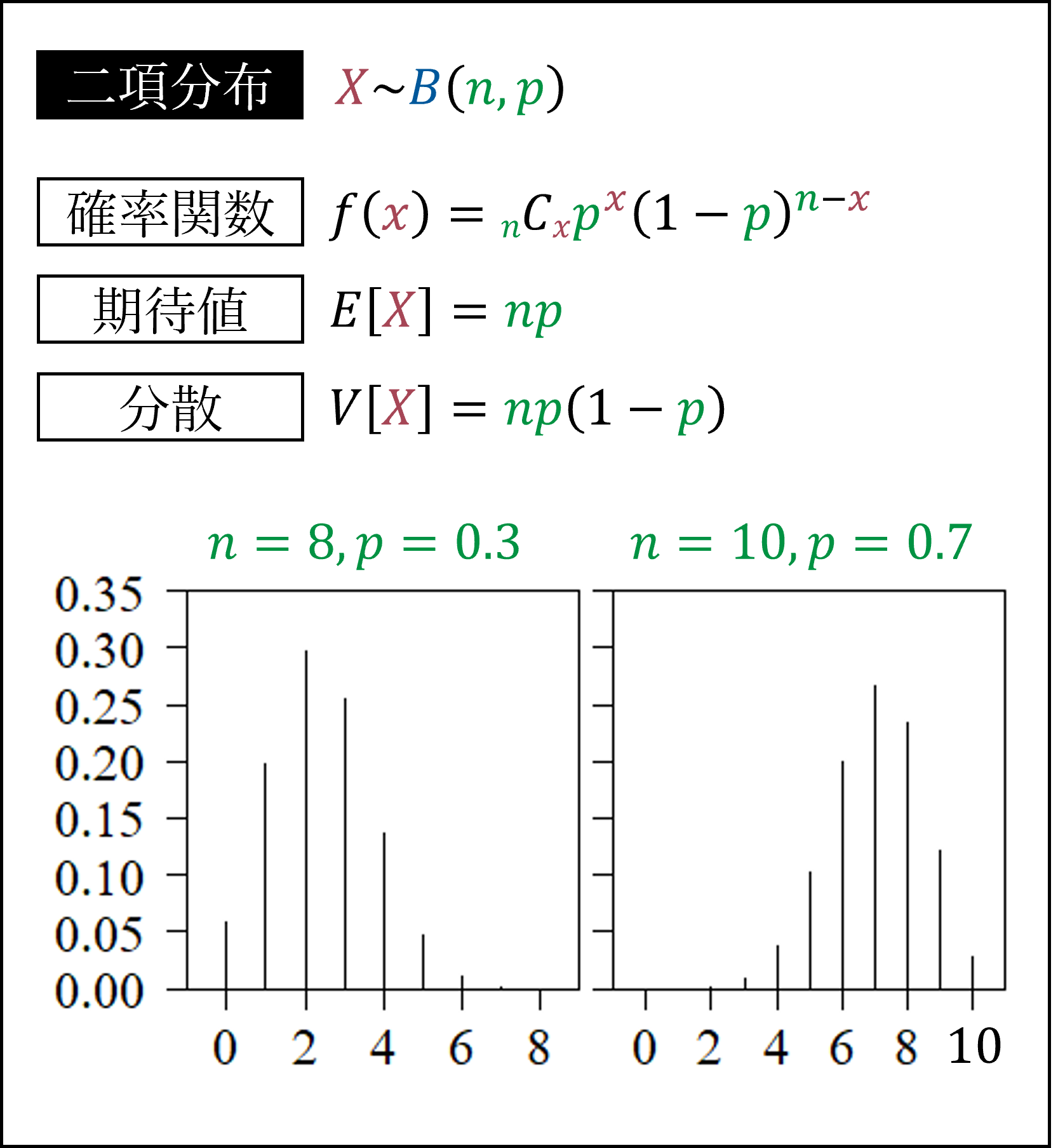
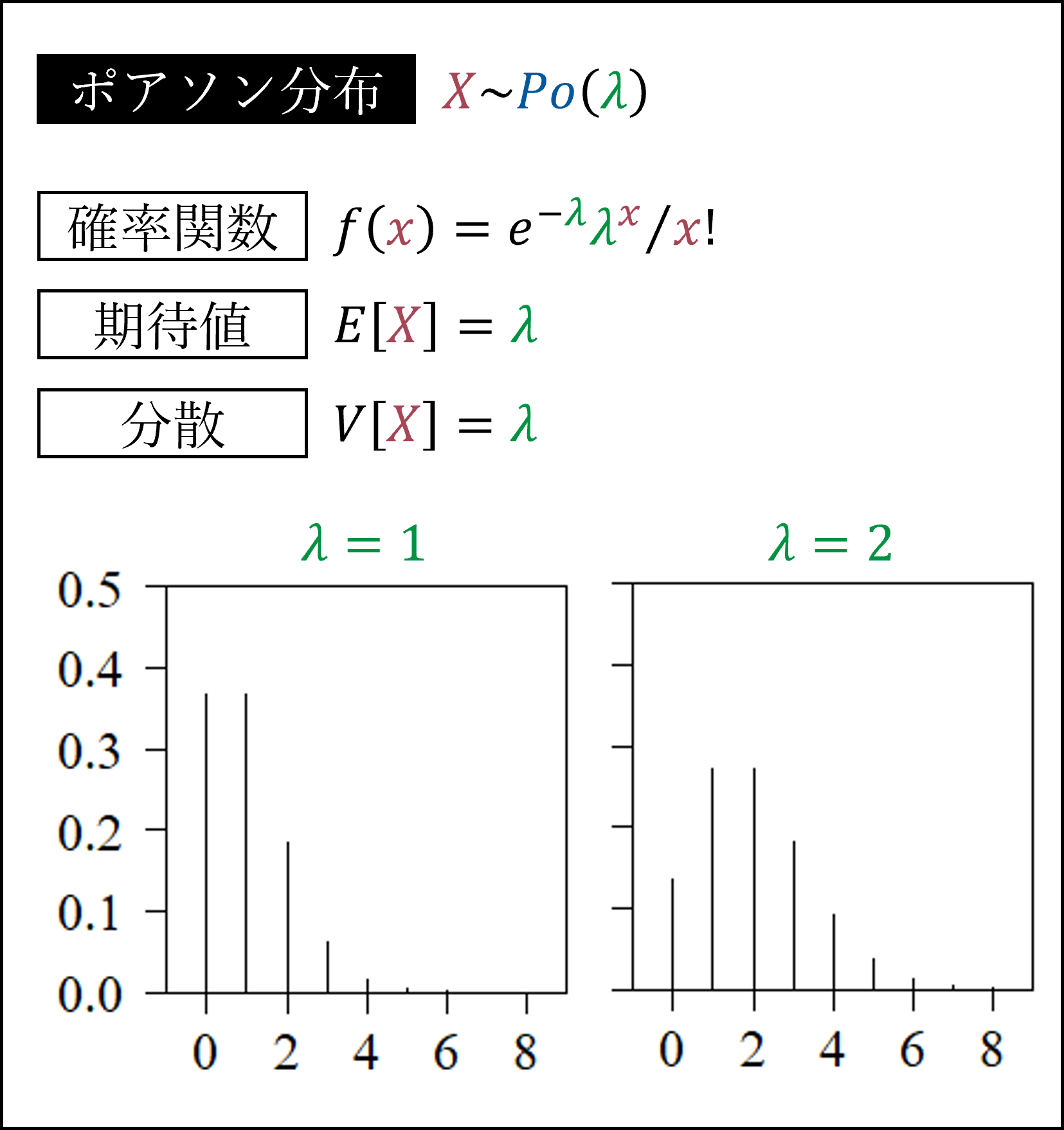
それからポアソン分布です。単位時間あたりの平均発生回数が一定（λ回）な事象がその単位時間において発生する回数（例：1日に平均1回交通事故が発生する交差点で、1日に交通事故が発生する回数）がしたがう分布になります。
最後に幾何分布です。成功確率pの事象を繰り返し試行したとき、初めて成功するまでに試行する回数（例：0.2の確率で当たるくじ引きを繰り返し引いて、初めて当たるまでにくじ引きを引いた回数）がしたがう分布になります。
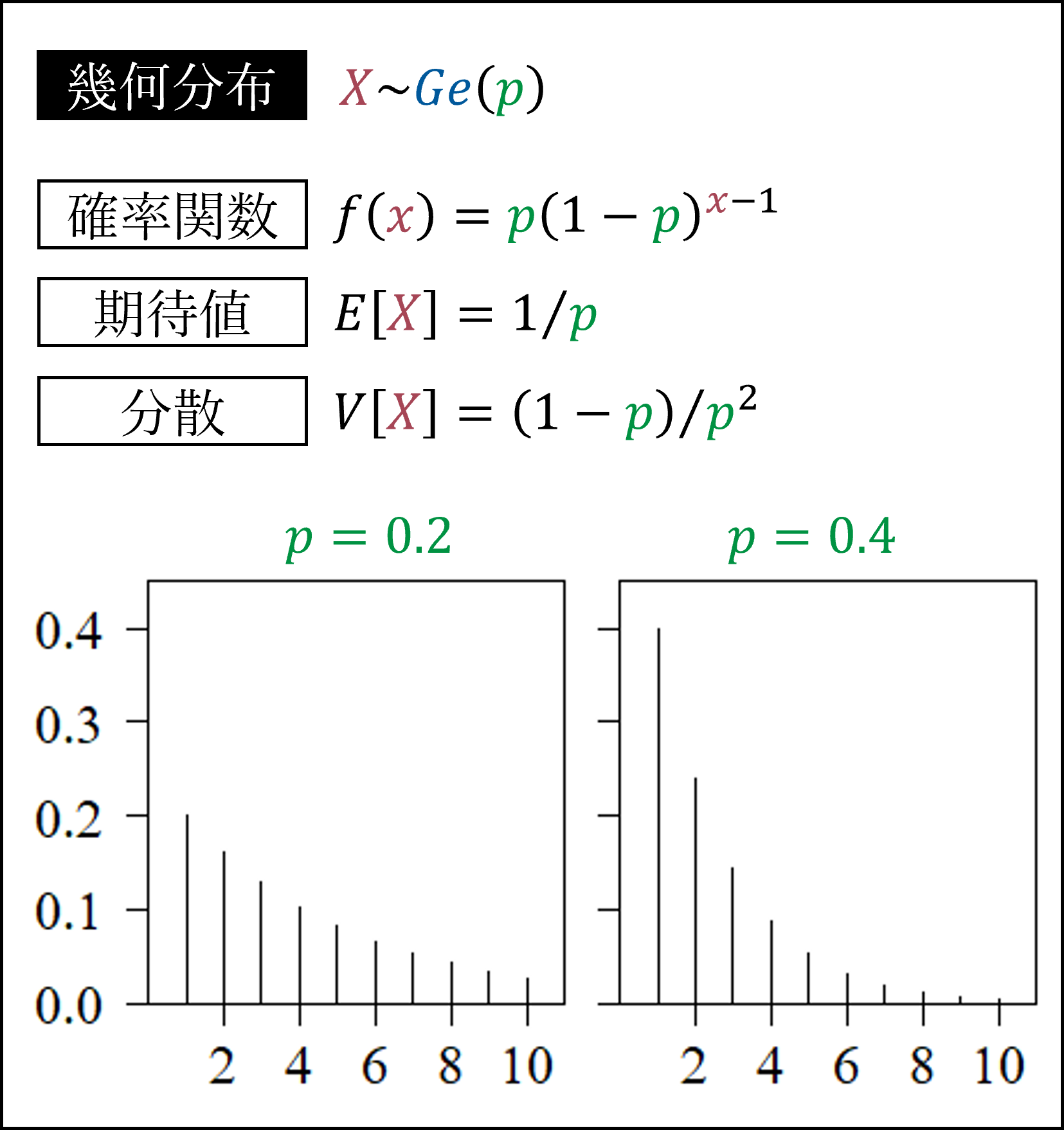
※初めて成功するまでの試行回数ではなく失敗回数をXとすることもあります。
(7) 連続型確率分布
ここから主な連続型確率分布を見ていきましょう。
まずは一様分布です。区間[a,b]において確率が一様な分布になります。
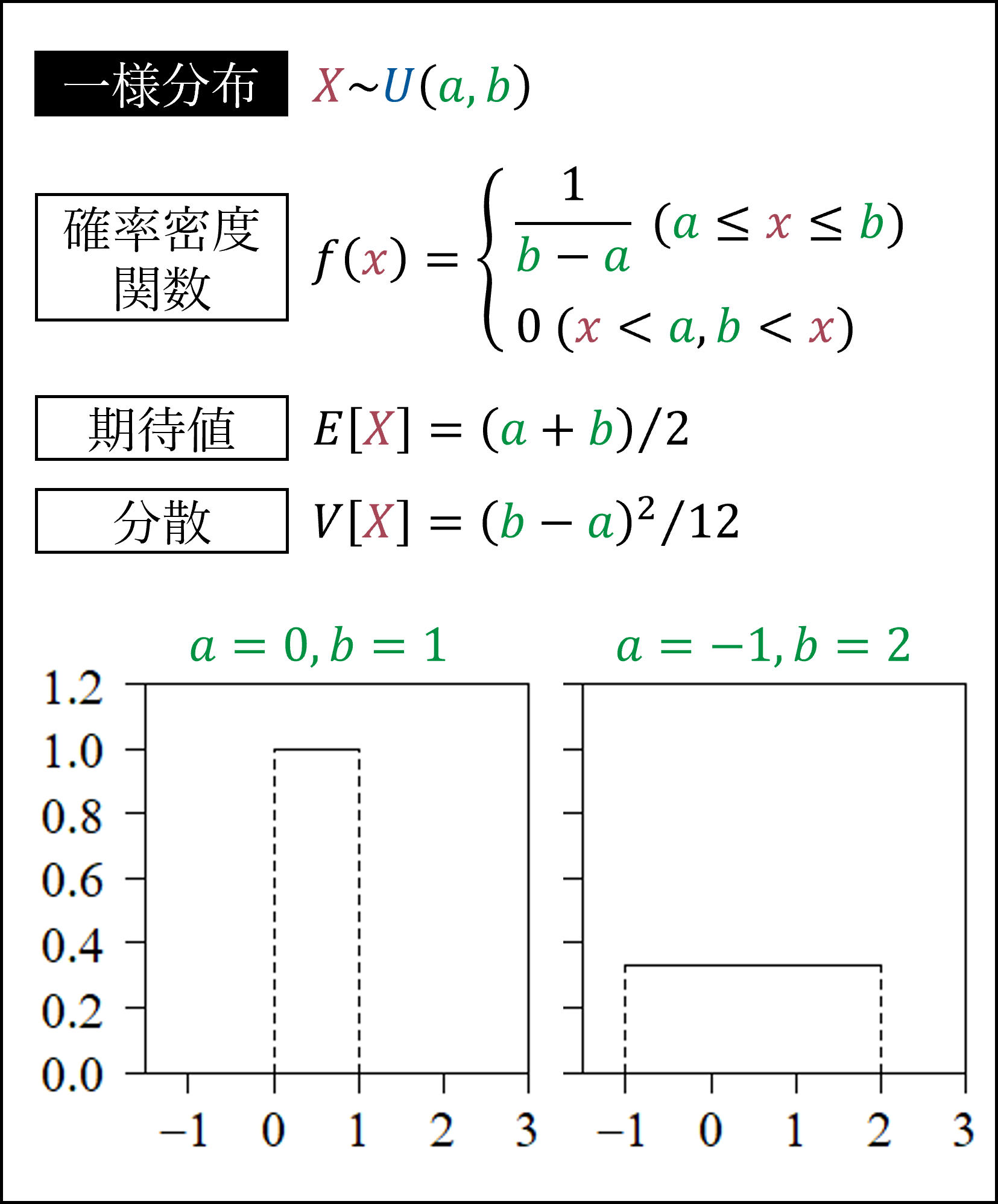
次に正規分布です。平均μを中心に左右対称な分布です。
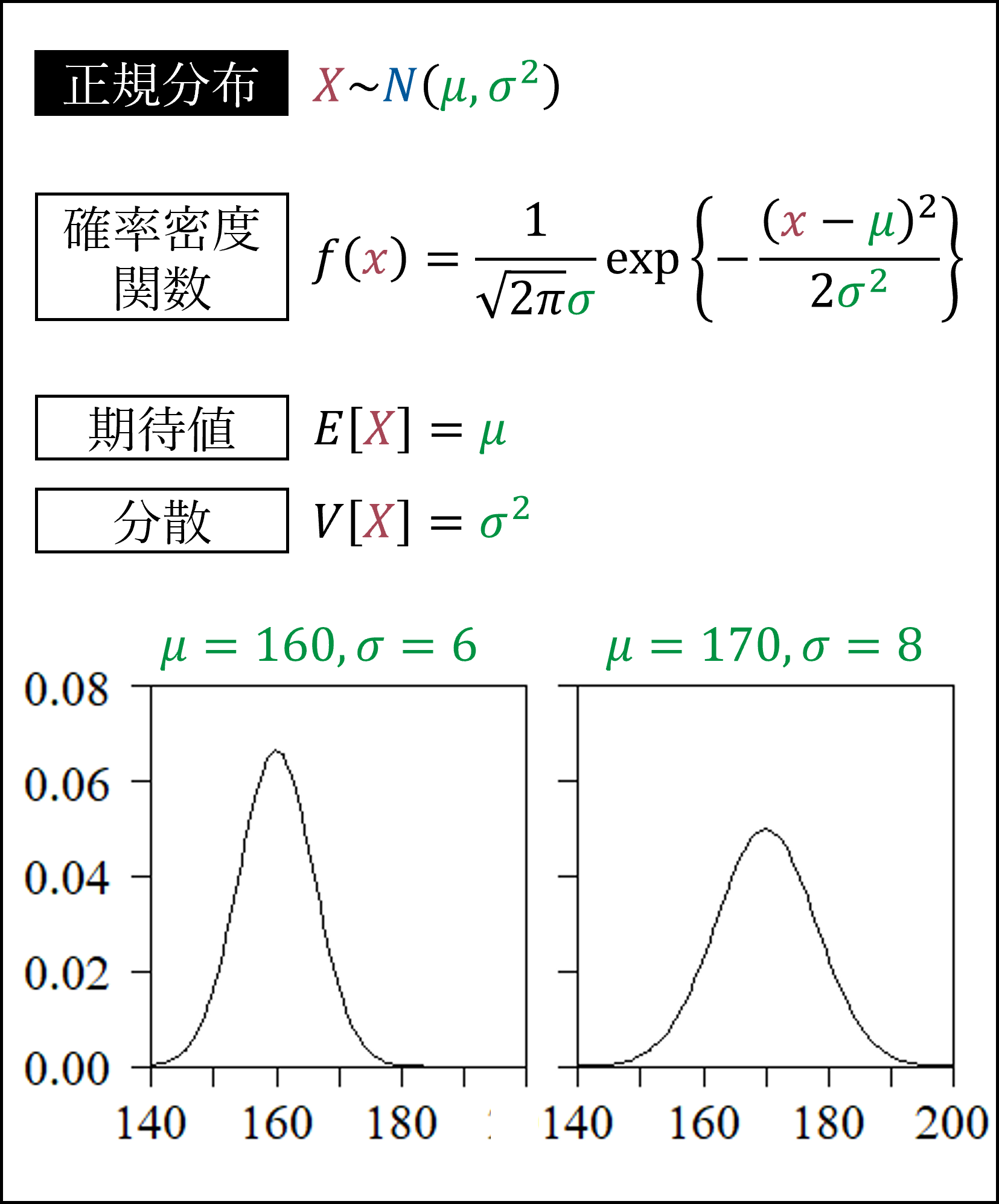
正規分布における「μ±σ」を変曲点と呼びます。正規分布の傾きは「μ-σ」で最大となり「μ+σ」で最小となります。
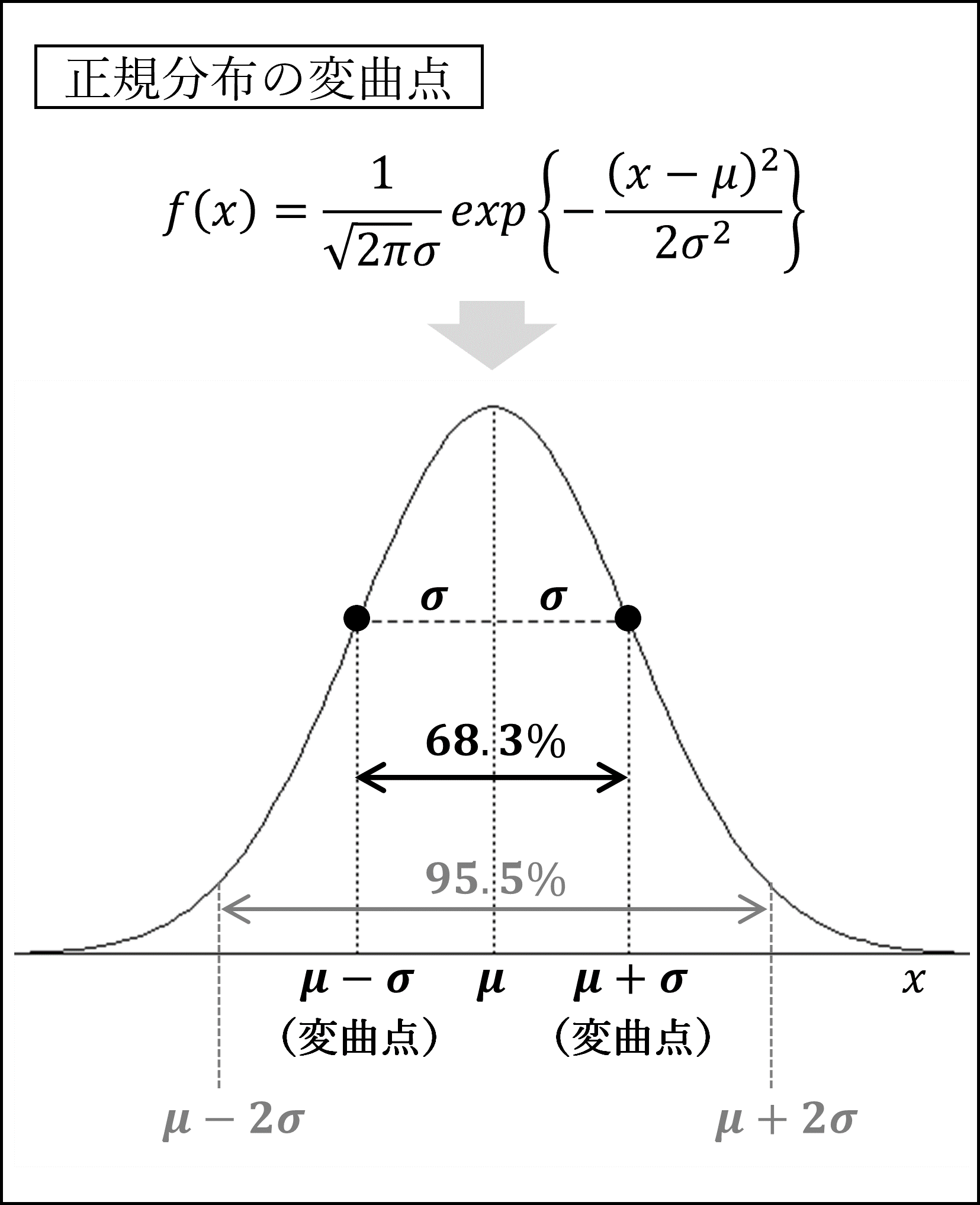
なお、正規分布にしたがう確率変数は「μ±σ」の範囲で約68.3%がカバーされ、「μ±2σ」の範囲で約95.5%がカバーされます。
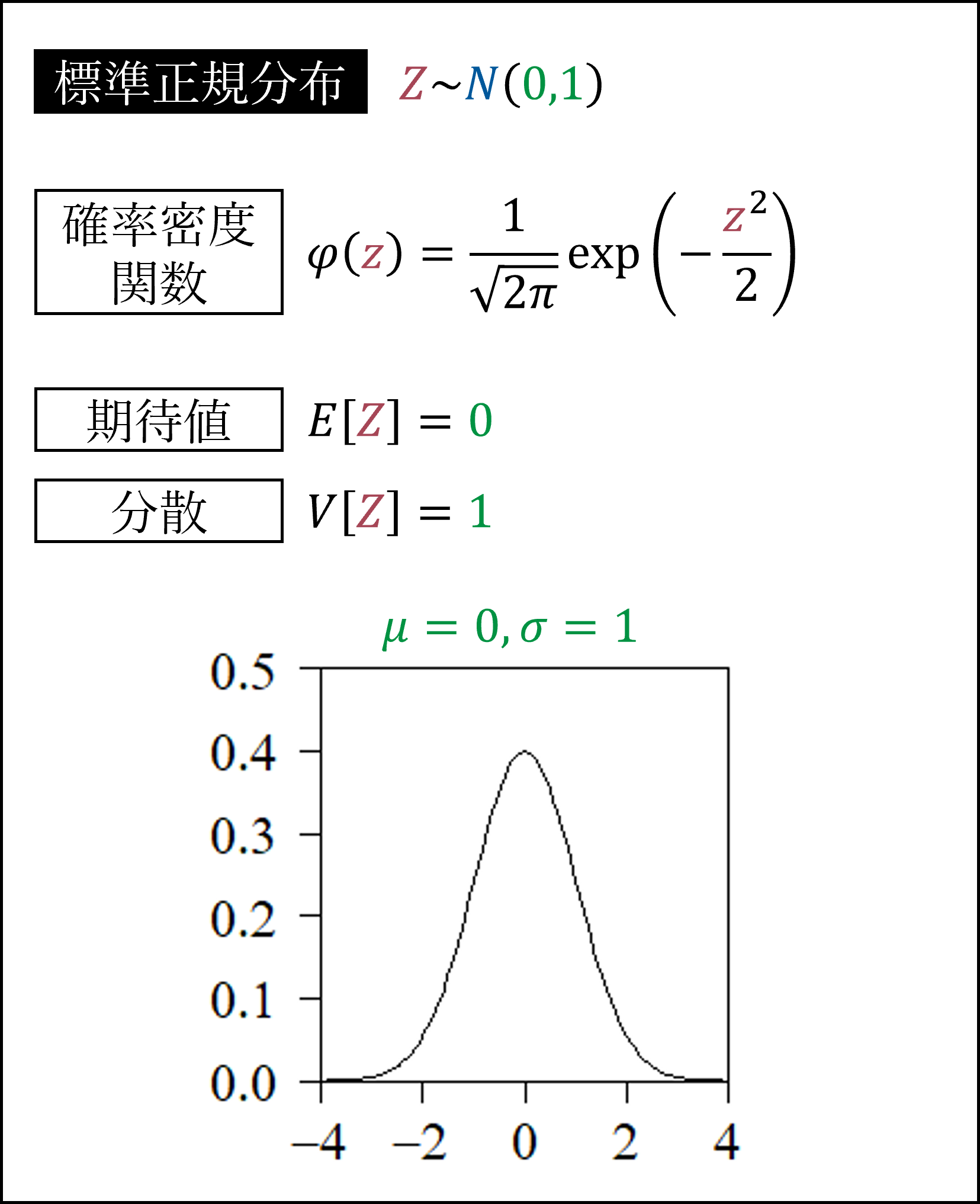
平均μ=0、分散σ^2=1の正規分布を標準正規分布と呼びます。
正規分布には再生性と呼ばれる性質があります。
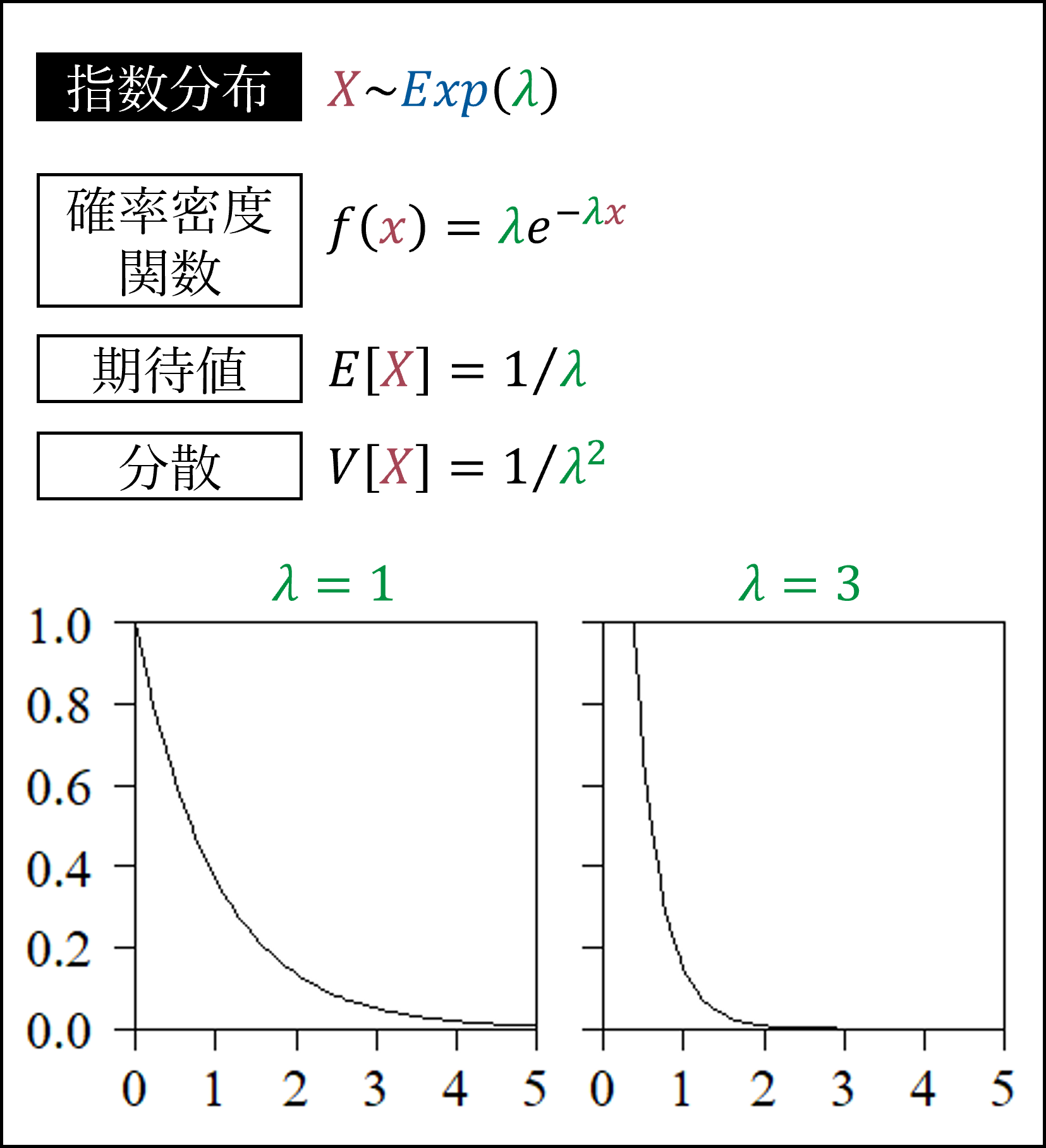
それから指数分布です。指数分布は単位時間あたりの発生確率が一定な事象が、このあと次に発生するまでの時間（例：1日に平均1回交通事故が発生する交差点で、このあと次に交通事故が発生するまでの時間(日数)）がしたがう分布です。
(8) 確率変数の和と平均
2つの確率変数の和の期待値と分散は以下のように計算されます。
※Cov[X,Y]はXとYの共分散を表します
なお、3つの確率変数の和の期待値と分散は以下のように計算されます。
また、線形結合された確率変数の和の期待値と分散は以下のようになります。
標本平均は確率変数の和を定数nで割った値（つまり「(nで割った)確率変数」の和）で、その期待値と分散は以下のようになります。
上記の期待値と分散が「標本平均の性質」として紹介されることが多いです。
(9) 標本分布
標本から計算される統計量がしたがう確率分布のことを標本分布と呼びます。
まずカイ二乗分布です。カイ二乗分布は標準正規分布にしたがう確率変数Zの二乗の和（平方和）がしたがう分布になります。
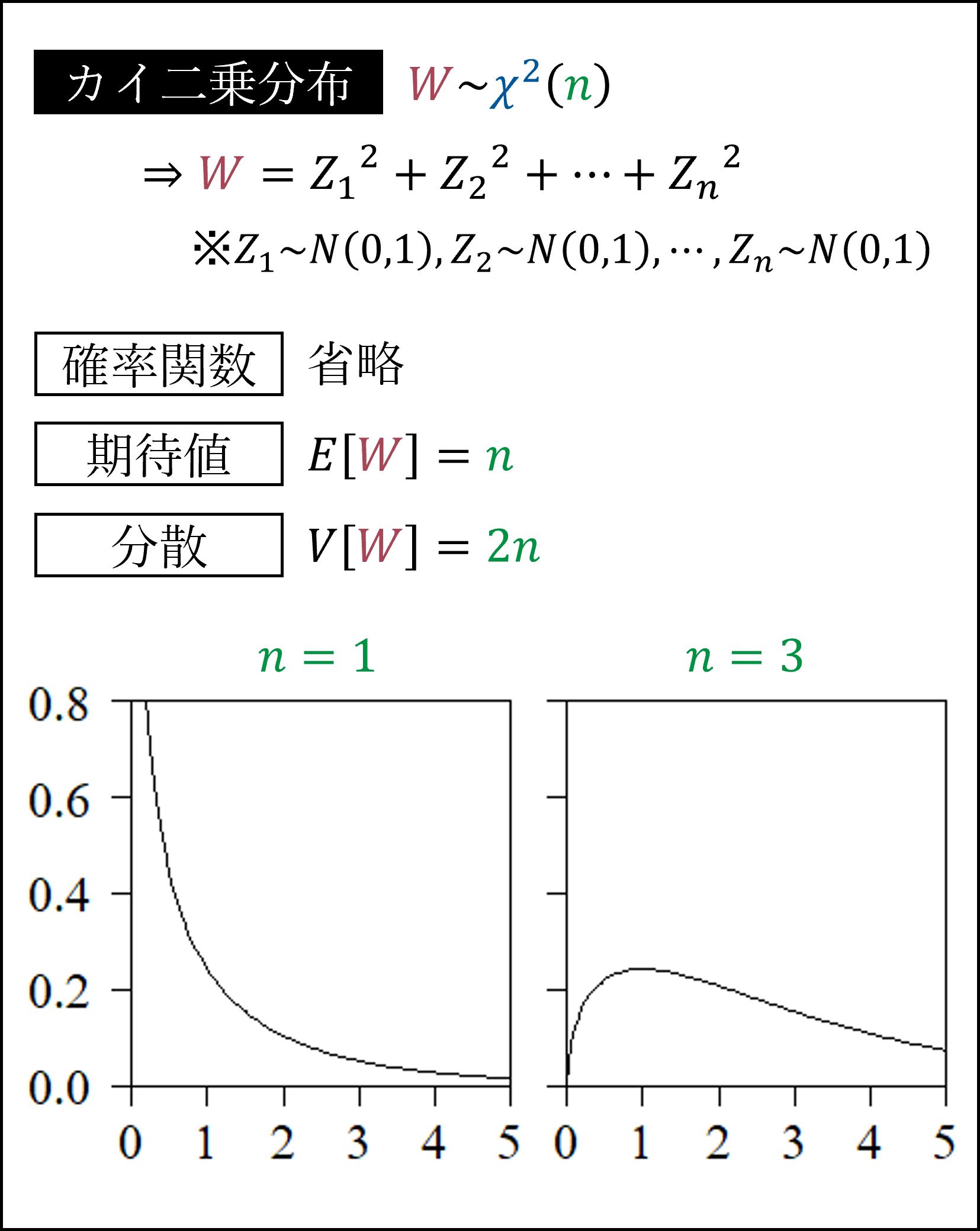
カイ二乗分布には再生性があります。
カイ二乗分布にしたがう統計量を2つご紹介します。
2つ目の式は母分散の区間推定や仮説検定の際に用いられます。
このほか適合度検定や独立性検定においてもカイ二乗分布が用いられます。
次にｔ分布です。ｔ分布は標準正規分布によく似た分布ですが、自由度が小さいときには標準正規分布に比べて分布の裾が厚くなります。
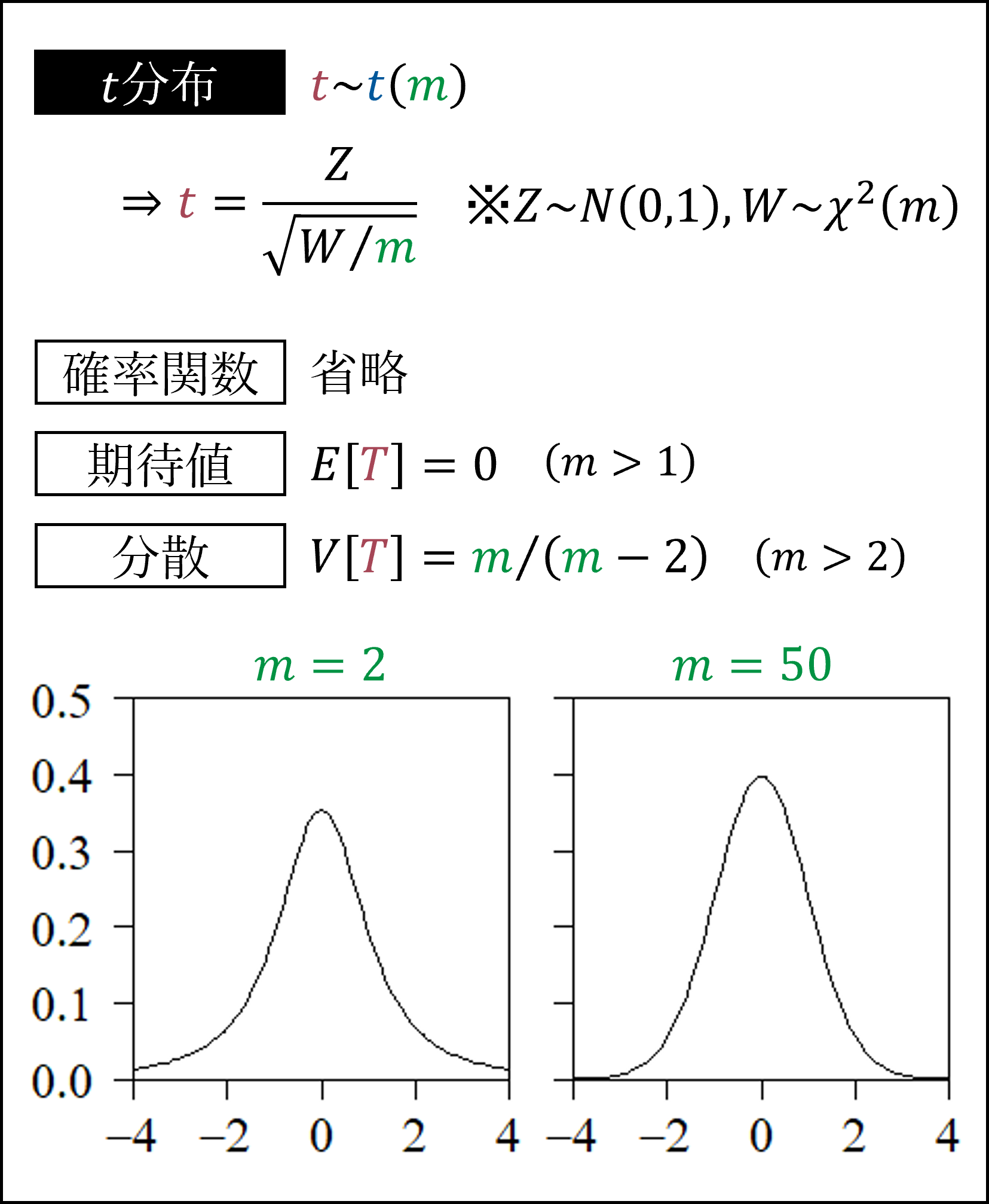
ｔ分布にしたがう以下の統計量は（母分散が未知でサンプルサイズが小さい場合に）母平均の区間推定や仮説検定に用いられます。
最後にF分布です。F分布はカイ二乗分布にしたがう確率変数を自由度で割って比をとった統計量がしたがう分布です。より端的に言うと「平均平方和の比」がしたがう分布です。
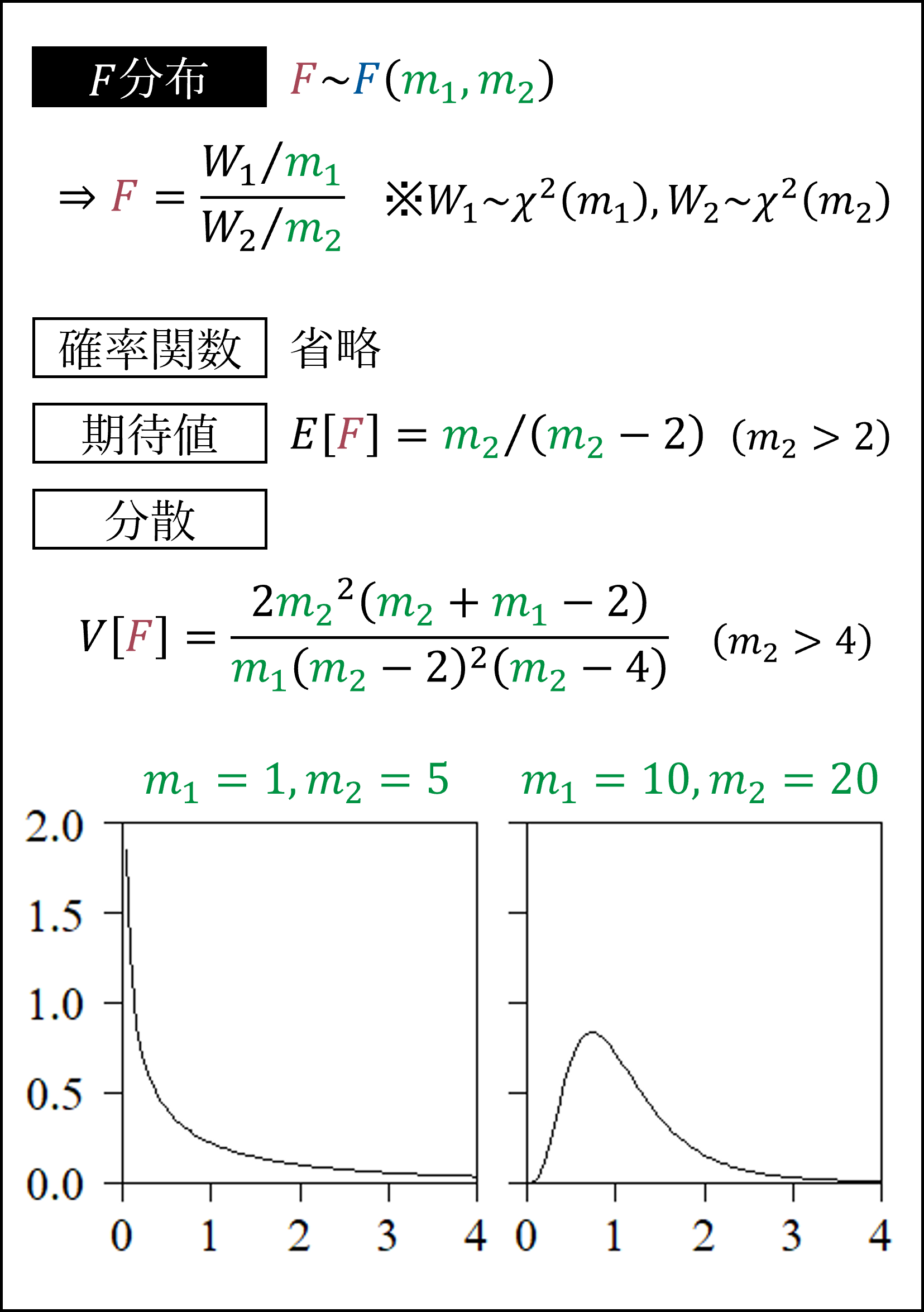
F分布にしたがう以下の統計量は母分散の比の区間推定や仮説検定に用いられます。
(10) 大数の法則
大数の法則はチェビシェフの不等式を用いて証明されます。
チェビシェフの不等式は以下になります。
チェビシェフの不等式を用いて「標本平均が母平均に確率収束する」ことが導かれ、これを大数の法則と呼びます。
大数の法則を以下の図で確認しておきましょう。
上図が元の母集団分布（母平均μ=170）を表し、下図がその母集団から抽出された標本（サンプルサイズn=100,n=1000,n=10000）の標本平均の分布を表しています。
サンプルサイズnが大きくなるほど確率分布が母平均に集まってきていることが分かるかと思います。
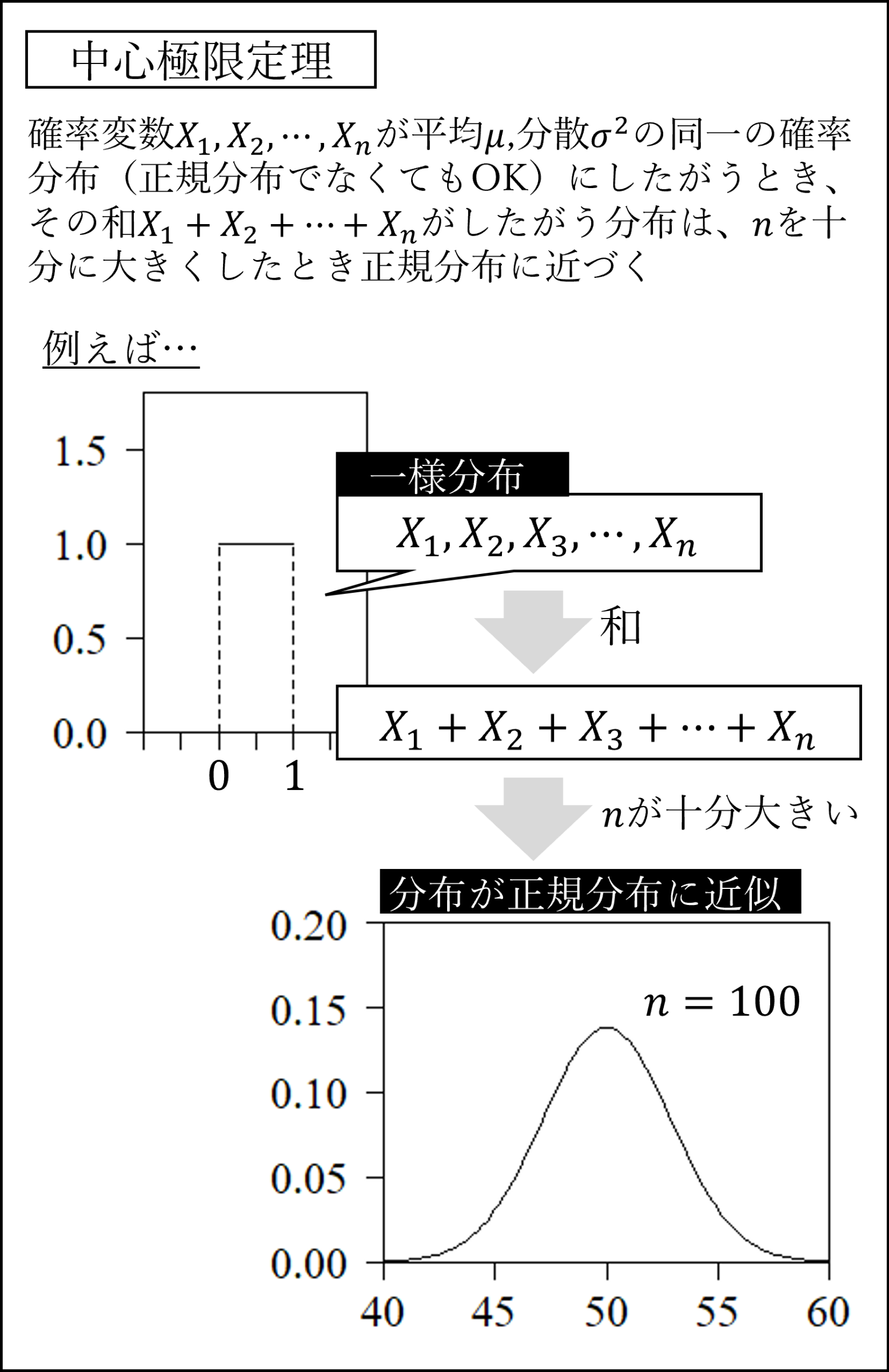
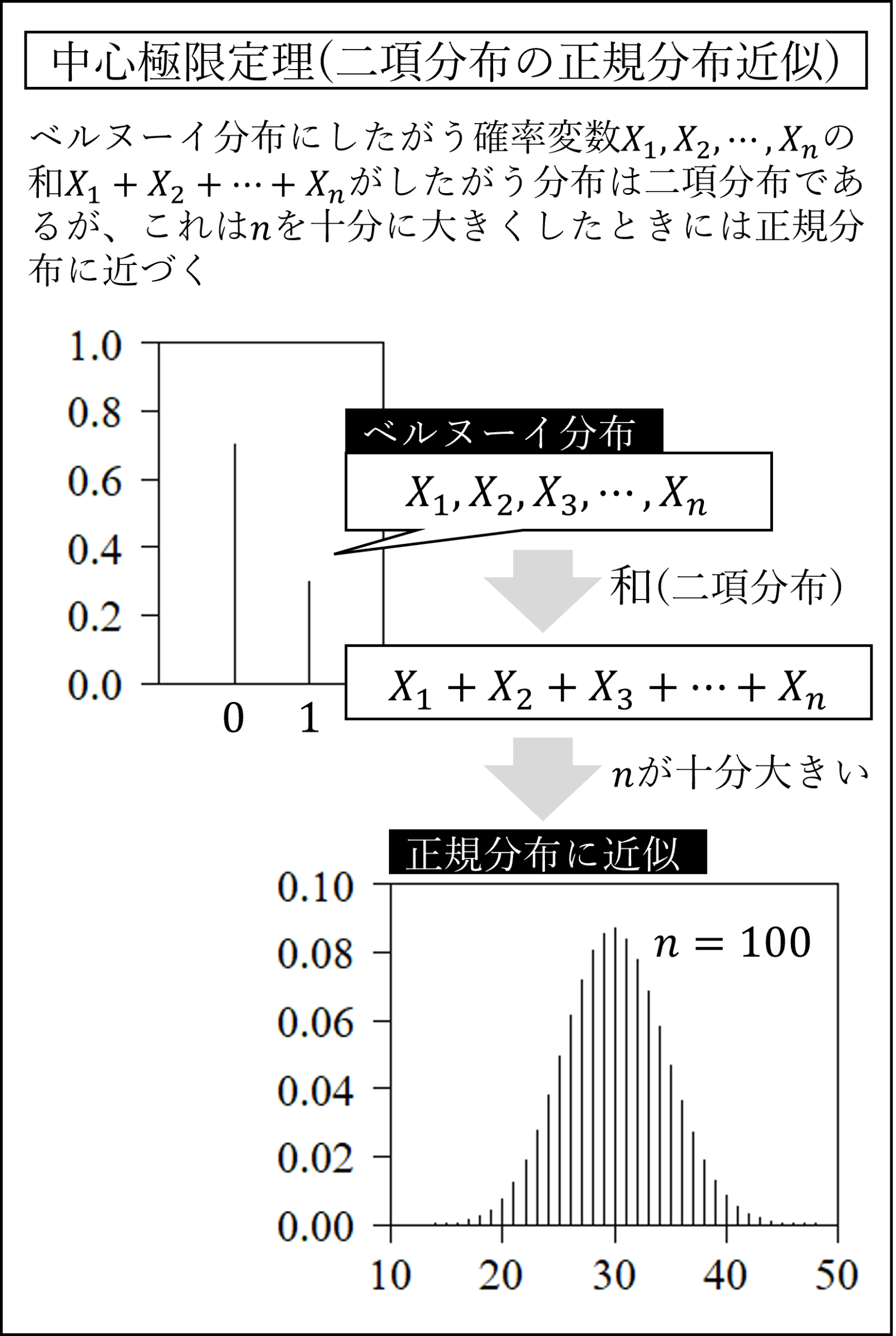
(11) 中心極限定理
独立なn個の確率変数の和の分布は（元の分布が正規分布でない場合でも）nが大きくなるにつれて正規分布に近づく性質のことを中心極限定理と言います。
二項分布はベルヌーイ分布の「和」ですので、試行回数nが十分大きいとき正規分布に近似します。
（「確率統計」は以上です）