
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問01 [01番](2021年6月試験)
テーマ
- (度数)分布の横軸と縦軸
- 平均値と中央値の性質の違い
- 歪度の特徴
正答
選択肢➀
解答例
消費者物価上昇率の度数分布の形状を問う問題です。
度数分布は、横軸が変数、縦軸が度数で、度数の合計がサンプルサイズ(データの数)になります。ここでは横軸が「消費者物価上昇率」、縦軸は「度数(横軸の消費者物価上昇率の各階級における頻度)」となり、1975年から2018年までのデータですのでサンプルサイズはn=2018-1975+1=44となります。
折れ線グラフを見ると、ほとんどの期間(具体的には1985年~2018年くらい)で消費者物価上昇率は0%を基準に約±2ptの幅におさまっています。したがって、度数分布における横軸が0%±2ptの区間の度数(縦軸)が多くなっていると推察できます。
一方で1975年~1980年ごろまでを見ると、消費者物価上昇率はかなり高くなっていて、1975年には12%近くの値となっています。したがって度数分布は右側(横軸の値が大きい側)に裾が長い分布になると推察できます。
まとめると度数分布は「横軸が0%±2ptに度数が多く分布しつつ、右側に裾が長く伸びている分布」になると推察できます。また、このような右に裾が長い分布における歪度は「正の値」となります。したがって、正答は選択肢➀となります。
補足
- 歪度の覚え方は「うっ・せい・わい(右・正・歪度=右に裾が長ければ正の値となるのが歪度)」
(01番以上)
問02 [02番](2021年6月試験)
テーマ
- 幾何平均
正答
選択肢②
解答例
1950年から1954年までの4年間の幾何平均 r(年次変化率)を計算する式は以下の通りです。
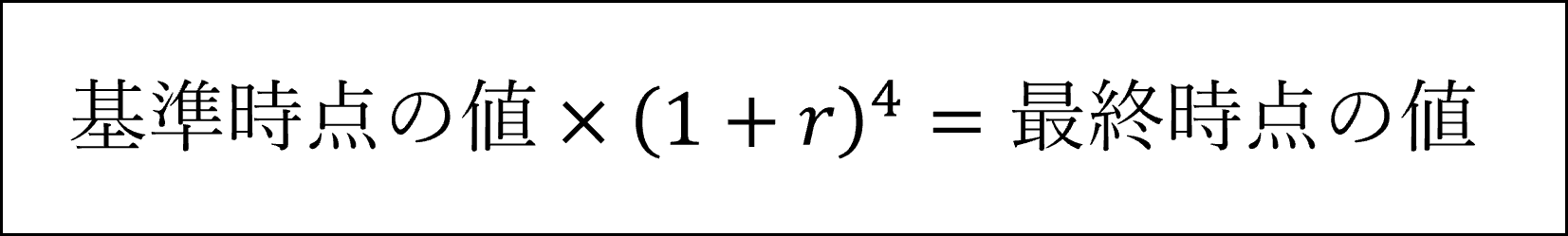
上記の式に、[基準時点の値]=115、[最終時点の値]=204 を代入して以下のように計算できます。
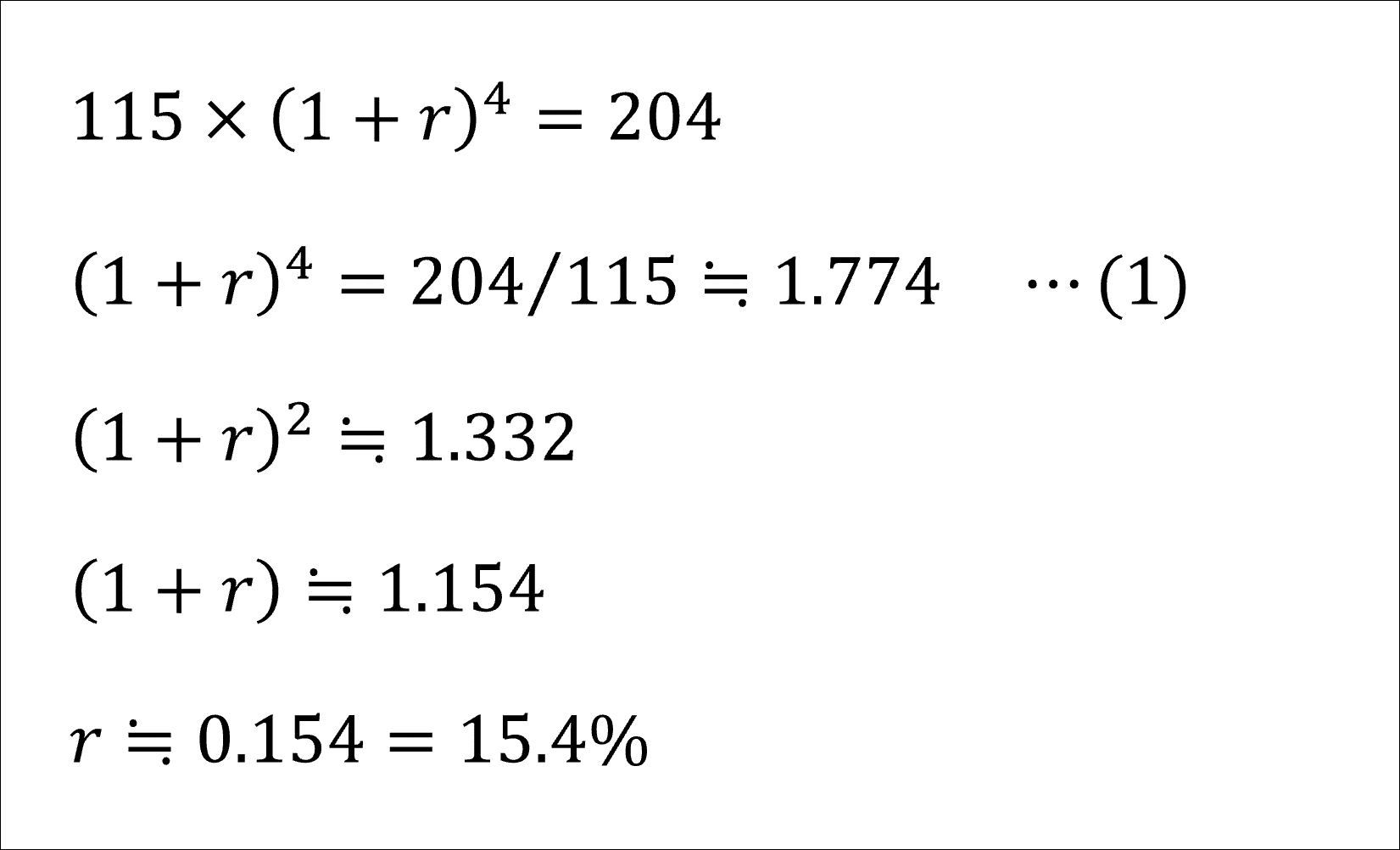
補足
- 電卓の√ボタンによって平方根を計算できます。
- したがって4乗根の計算(4乗を1乗に戻す計算)は√ボタンを2回押すことで計算できます(4乗→2乗→1乗)。
- もしくは選択肢を利用して、各選択肢の値に1を足した値(1+r)を電卓で4乗して([値]を入力→[×]ボタンを押す→[=]ボタンを押す→[=]ボタンを押す→[=]ボタンを押す)、(1)式の1.774に最も近いものを選ぶ…という方法もあります。
(02番以上)
問03 [03番](2021年6月試験)
テーマ
- 価格指数の計算
- パーシェ式指数の計算式
正答
選択肢②
解答例
パーシェ式の価格指数(財の種類がXとYの2種類の場合)は以下の計算式により計算できます。

したがって、本問におけるパーシェ指数(パーシェ式価格指数)は
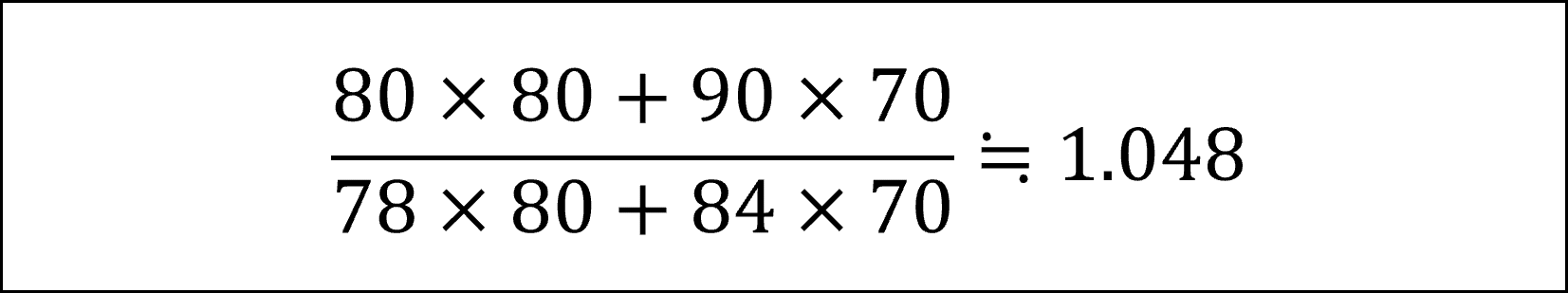
と計算されます。なお、本問では指数を100としていますので、上記の1.048に100を掛けて正答は104.8となります。
補足
価格指数はラスパイレス式やパーシェ式の公式を覚えて計算すれば解答できますが、そもそもラスパイレス式とパーシェ式は何がどう違うのか、という点も重要になります。ぜひラスパイレス式やパーシェ式の計算方法の意味についても調べてみましょう(このブログでも関連記事を書きたいと思います)。
(03番以上)
問04 [04番](2021年6月試験)
テーマ
- 割合の計算
- 指数の読み取り
正答
選択肢③
解答例
まず、1990年の全国の新聞発行部数の13%が東京都の新聞発行部数という情報から、1990年の東京都の新聞発行部数の実数を以下の式により計算します。
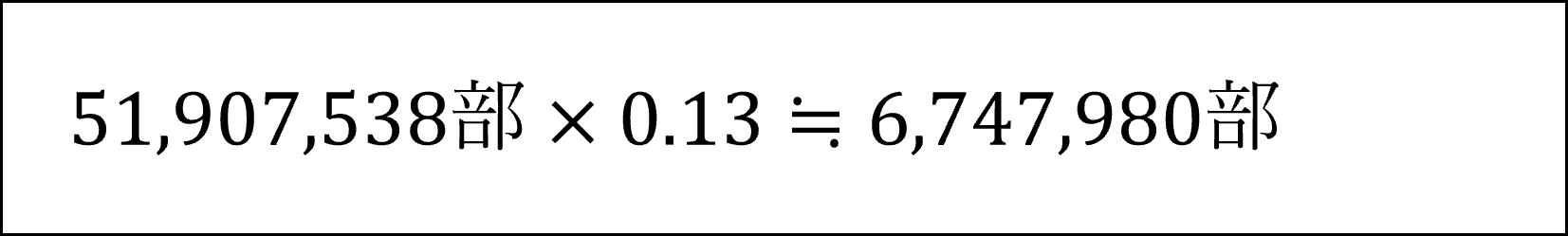
そのうえで2019年の指数(およそ57)から2019年の東京都の新聞発行部数の実数を以下の式により計算します。
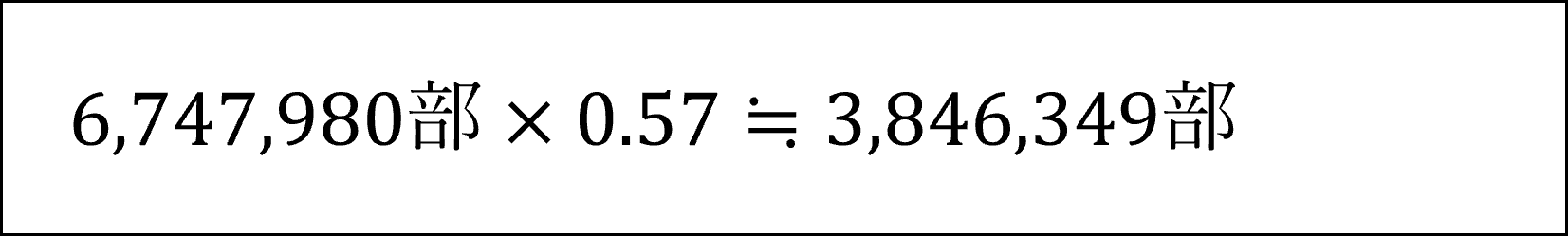
最後に1990年から2019年の増減を以下の式により計算します。
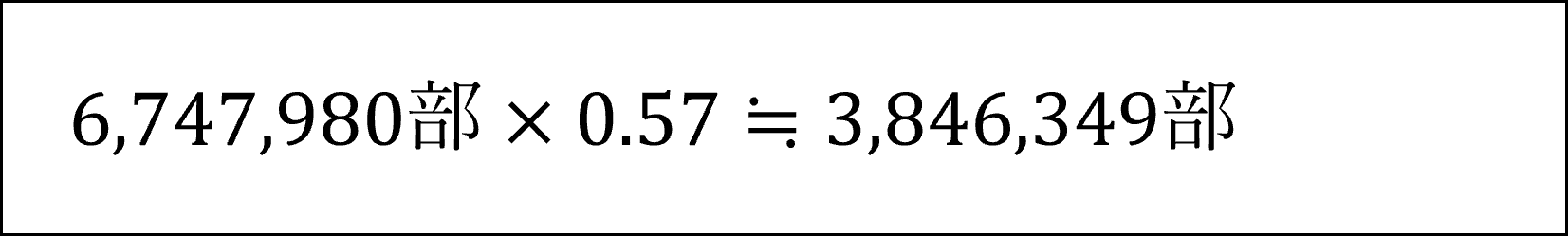
以上より、選択肢③が正答となります。
補足
- 本問のような大きな値の数字の計算はミスをしがちです。焦らずに式をメモ用紙に下書きしてから電卓で計算することをおすすめします。
- 2019年の東京都の発行部数が選択肢に用意されており、最後の「増減」の計算を忘れて誤答してしまうミスを誘っています。大きな値の数字の計算は、選択肢に「ぴったし」の値があると飛びついてしまいがちですので気をつけましょう。
(04番以上)
問04 [05番](2021年6月試験)
テーマ
- 指数の推移から前年比増加率を読み取れるか
- 前年比増加率の推移の縦軸を理解できるか
正答
選択肢➀
解答例
前年比増加率の推移を表したグラフの横軸は「年」で、縦軸は「前年比増加率」になります。
縦軸の「前年比増加率」が0%より上側にあれば前年比で増加していて、0%より下側にあれば前年比で減少していることになります。
問題に与えられた1990年を100とした指数のグラフを見ると、東京都では前年比で増加した年(つまり1つ前のプロットよりも上側にプロットされている年)は1990年・1993年・1996年・2001年・2004年の5つの年のみです。
したがって、この5つの年(1990年・1993年・1996年・2001年・2004年)で縦軸が0%より上側にある選択肢を探すと、正答が➀であることが分かります。
なお、東京都では2018年に顕著に減少していることもあわせて考慮すると、より安心して選択肢➀を選ぶことができます。
補足
- グラフの読み取り問題は「鳥の目と虫の目」の双方が問われます。
- 本問では「鳥の目」で全体的に減少傾向であることを読み取り、「虫の目」で各年の増減動向を確認する必要があります。
(05番以上)
問05 [06番](2021年6月試験)
テーマ
- 散布図の2軸の確認
- 散布図からの相関係数の読み取り
- 散布図からの回帰直線の当てはめ
正答
選択肢⑤
解答例
Ⅰ:正しいです。分散とは「平均からの偏差の二乗の合計をサンプルサイズで割ったもの」で、値がどれくらいばらついているかを示します。
横軸に飛距離点、縦軸に飛型点をとった散布図を見ると、横軸の飛距離点の値の幅はおよそ20~80点であるのに対し、縦軸の飛型点の値の幅はおよそ46~56点ですので、前者の分散の方が大きくなることが分かります。
Ⅱ:正しいです。相関係数は「2変数の平均からのばらつき方がどれくらい似通っているか」を示す指標で、直線上にプロットが集まっているほど相関係数(の絶対値)は高くなります。
2つの散布図を比較すると、飛距離点と飛型点の散布図の方が直線上にプロットが集まっていることがわかります。
Ⅲ:正しいです。回帰直線の切片(厳密には”y切片”)は、回帰直線において、横軸(x)の値に0を代入したときの縦軸(y)の値になります。
飛距離点と飛型点の散布図から、横軸の飛距離点が20点から80点へと60点増加すると、縦軸の飛型点が46点から56点へとおよそ10点増加するような関係性を読み取れます。つまり、回帰直線を当てはめたときの傾きはおおよそ10/60となると推察できます。
したがって、横軸が0点となるときの縦軸の値(y切片)は、横軸が20点のときの縦軸の値(およそ46点)から「-20点×10/60」だけ小さくなると推察できます。
これを計算すると、46点-20点 × 10/60 = 46点-10/3点 ≒ 43点となり、y切片が正の値になるとわかります。
補足
- 散布図も「鳥の目」と「虫の目」で読み取りましょう。
- その際、まずは「鳥の目」でみて、そのあとに「虫の目」を使いましょう。
- 本問では「鳥の目」ですべての設問が正しいと読み取ることができますので、「虫の目」を使う時間を節約できます。
(06番以上)
問05 [07番](2021年6月試験)
テーマ
- 3つの変数の整理
- 共分散の式変形
- 分散の式変形
- 相関係数の式変形
正答
選択肢④
解答例
飛距離、飛距離点、飛型点という3つの変数が登場し、飛距離がx、飛距離点がyと定義されています。飛型点は問題文中に記号で定義されていませんので、飛型点をzと定義しておきましょう。
まず、(ア)は1/2(倍)となります。飛距離xと飛型点zの共分散をCox[x,z]とおき、飛距離点yと飛型点zの共分散Cov[y,z]とおくと、Cov[x,z]=(1/2)×Cov[y,z]と整理できるため、「1/2(倍)」となります。具体的な式変形は以下の通りです。

また、(イ)は1(倍)となります。飛距離xと飛型点zの相関係数をρ[x,z]※とおき、飛距離点yと飛型点zの相関係数をρ[y,z]とおくと、ρ[x,z]=ρ[y,z]と整理できるため、「1(倍)」となります。具体的な式変形は以下の通りです。

※ρという記号は「ロー」と呼び、(母)相関係数の記号として用いられることの多い記号になります。
補足
- 本問のような変数の定数倍(2Xとか3Yとか)の共分散や分散を計算させる問題は頻出です。
- 飛型点をzとおいて整理して落ち着いて式を整理していきましょう(複数の変数が登場した場合は記号で置き換えてあげるクセをつけておきましょう)。
(07番以上)
問06 [08番](2021年6月試験)
テーマ
- 相関係数の式変形
- Σ記号の計算
- 不偏分散の分母
正答
選択肢③
解答例
相関係数の式を愚直に変形していきましょう。まず相関係数の分子である「xとyの共分散Cov[x,y]」を以下のように計算します。

ここで、

を(1)式に代入して

一方で相関係数の分母の「xの標準偏差とyの標準偏差の積」は

ここで、

を(2)式に代入して

以上より、相関係数は

補足
- 計算力が問われる問題です。(1)の式を導くのに苦労するかもしれませんが、Σ記号に慣れておくと見た目ほど難しくはないと思います。
(08番以上)
問07 [09番](2021年6月試験)
テーマ
- 層化抽出法
- 層化二段抽出法
- 集落抽出法
正答
選択肢④
解答例
母集団である社員全体から、母集団をよく代表してくれるような標本を抽出しようというシチュエーションです。
(ア)は事業部という層に分けたうえでいくつかの事業部を無作為抽出していることから、層化抽出法になります。
(イ)は1段階目として事業部という層で無作為抽出を行う、その後、2段階目として抽出した各部(層)において社員を抽出していますので、層化二段抽出法になります。
なお、集落抽出法はクラスター抽出法とも呼ばれ、抽出した集落(クラスター)を全数調査するという特徴があります。集落内を「全数調査」するという点がポイントです。
補足
- 標本抽出法はほぼ必ず出題されてきた分野ですので、とりこぼしのないように論点をおさえておきましょう。
(09番以上)
問08 [10番](2021年6月試験)
テーマ
- 同時確率関数の計算
- 相関係数の計算
- 独立性の定義
正答
選択肢⑤
解答例
与えられたXとYの同時確率関数f(x,y)から、X^2とY^2の同時確率関数f(x^2,y^2)を以下のように整理できます。
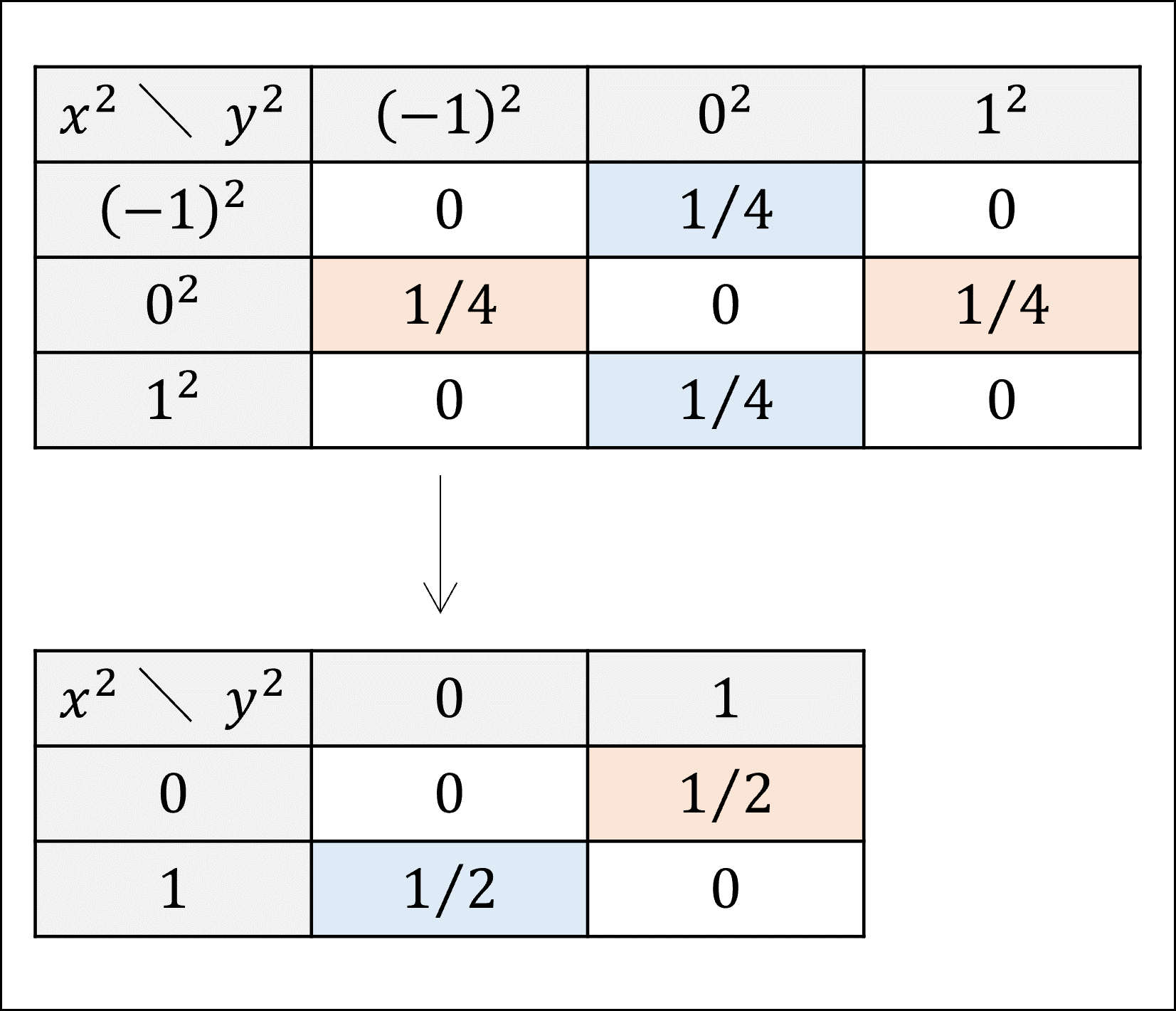
この表を横軸をx^2、縦軸をy^2とする散布図に落とし込むと以下のようになります。

上図の通り、(x^2, y^2)=(0, 1)または(1, 0)となる2点のみに分布することになり、x^2とy^2には完全な直線上の関係が認められます。
つまり、x^2とy^2には(負の)相関関係があることになり、相関係数は-1となります。
また、相関係数が0ではないのでx^2とy^2は互いに独立ではありません。
補足
- 具体的に相関係数を計算して解くこともできますが、上記のようにx^2とy^2の同時確率分布の表を作成してしまう方が効率的に解答できます。
(10番以上)
問09 [11番](2021年6月試験)
テーマ
- 確率計算
- 余事象の発想
- 階乗の計算
正答
選択肢⑤
解答例
誕生日が同じになるときの誕生日の組み合わせのパターンを考えたくなりますが、その計算は重労働で途方に暮れてしまいます。計算が重労働に感じたときはぜひ「余事象」に着目しましょう。
本問での「余事象」は「同じ誕生日の人が存在しない」ですので、この確率を計算して1から引いてあげれば「同じ誕生日の人が存在する確率」になります。具体的な計算式は以下の通りです。

補足
- 「同じ誕生日の人が存在しない」確率は、1人目の誕生日が1月1日であれば、2人目の誕生日は365日のうちの1月1日以外の364日間のいずれかの日(364/365)になります。そして2人目の誕生日が1月2日であれば、3人目は1月1日と1月2日以外の363日のうちのいずれかの日(363/365)になります。4人目以降も同様に考えていくと、上記の計算式となります。
- なお1人目の誕生日は365日のうちのいずれの日でもよいので、計算式における確率は365/365(=1)となります。
- 階乗の計算にも慣れておきましょう。
(11番以上)
問10 [12番](2021年6月試験)
テーマ
- 標準化(平均を引いて標準偏差で割る)
- 標準正規分布の付表の読み取り
正答
選択肢④
解答例
確率変数Xが正規分布N(60, 9^2)にしたがいますので、確率変数を標準化した(平均を引いて標準偏差で割った)(X-60)/√(9^2)が標準正規分布N(0, 1)にしたがいます。
これを念頭に与えられた条件を以下のように整理しなおします。

ここで標準正規分布の付表より、標準正規分布にしたがう確率変数zがz=2.29となるときに上側確率※が0.011であることを読み取れます。標準正規分布は左右対称の分布ですので、z=-2.29となるときの下側確率※も0.011ということになります。
上記の(1)式においては、(X-60)/9が標準正規分布にしたがう確率変数ですので、これが-2.29以下となる確率が0.011ということになります(以下の(2)式)。したがって、(1)式を満たす定数cの値は以下のように計算できます。

※上側確率:確率変数がその値よりも大きな値となる確率
※下側確率:確率変数がその値よりも小さな値となる確率
補足
- 試験では確率の計算をExcelやRといったソフトウェアに頼ることができませんので、手元に与えられる「付表」を用いて確率を導く必要があります。
- 何がどんな分布にしたがうかを整理し、さらにそれを標準正規分布などの付表が与えられた標本分布にしたがうかたちに整理することで具体的な確率を確認することができます。
- スタートは「何がどんな分布にしたがうか」で、ゴールは「付表を用いた具体的な確率の確認」というイメージをもっておきましょう。(いきなり付表を使おうとするのでなく…)
(12番以上)
問11 [13番,14番](2021年6月試験)
テーマ
- 累積分布関数の図示
- 一様分布の期待値
正答
[13番]選択肢① [14番]選択肢③
解答例
与えられた条件から、累積分布関数を以下のように図示できます。

[13番]上図より横軸のxが1より大きくなる領域において、縦軸のF(x)はまったく増加していません(つまり、確率が蓄積されていない)ので、P(X > 1)、すなわち、Xが1より大きくなる確率は0となります。
[14番]また、上図より横軸のxの区間[0,1]において、xの増加に比例して縦軸のF(x)も増加していることがわかります。これは言い換えると、区間[0,1]において、どんなxの値においても一様に確率が分布しているということになります。具体的な確率分布は以下の図のようになります。

上図のように一様に確率が分布しているときの確率分布を一様分布といい、区間[a,b]の一様分布の期待値は(a+b)/2ですので、以下のように期待値を計算できます。

補足
- 累積分布関数F(x)は確率変数Xについて値の小さい側(下側)からX=xまでの確率を累積したものを表します。例えば標準正規分布であれば、値の小さい側からX=0までの累積の確率がちょうど半分の0.5になりますので、累積分布関数F(0)=0.5となります。
- 本サイトでは確率分布に関して「確率が分布する」という表現を頻繁に用いています。確率の神様が確率(密度)関数というルールに従って確率をばらまいて分布させているイメージをもつとわかりやすいです(わかりにくいという場合はスルーしていただいて大丈夫です)。
- 確率分布の下側の面積(上図の「S」)が1となることを用いると、計算が容易になることがあります。
(13番,14番以上)
問12 [15番,16番](2021年6月試験)
テーマ
- 幾何分布の確率関数と期待値
- 標本平均の性質
- チェビシェフの不等式
- 大数の法則
正答
[15番]選択肢③ [16番]選択肢④
解答例
与えられた確率関数から、母集団は成功確率p=1/3の幾何分布(初めて成功したときの試行回数xがしたがう分布)であることがわかります。
[15番]幾何分布の平均(期待値)は1/pですので、母平均、つまり、成功確率p=1/3の幾何分布にしたがう母集団の平均(期待値)は1/p=1/(1/3)=3となります。
[16番] 標本の大きさnが極めて大きいとき(無限大にしたとき)、標本平均は母平均に収束していきます。これを大数の法則と呼びますが、この大数の法則はチェビシェフの不等式を用いて証明されます。
チェビシェフの不等式は以下になります。

このチェビシェフの不等式における確率変数Xを標本平均におきかえて考えます。本問における標本平均の期待値は3で、標本平均の分散は6/n※となりますので、チェビシェフの不等式を以下のように書き換えることができます。

以上より、正答は6/(nε^2)となります。
※標本平均の分散は、標本を抽出するもととなる母集団の分散(母分散)を標本のサンプルサイズnで割った値となります。
補足
- [16番]は難問です。標本の大きさnが極めて大きいとき(無限大にしたとき)、標本平均は母平均に収束していきます(大数の法則)。この法則はチェビシェフの不等式を用いて証明されます。この流れを学習していなければ一体何の話をしているのか混乱してしまうと思います。
- 例えばεに0.1を代入すると以下のようになります。
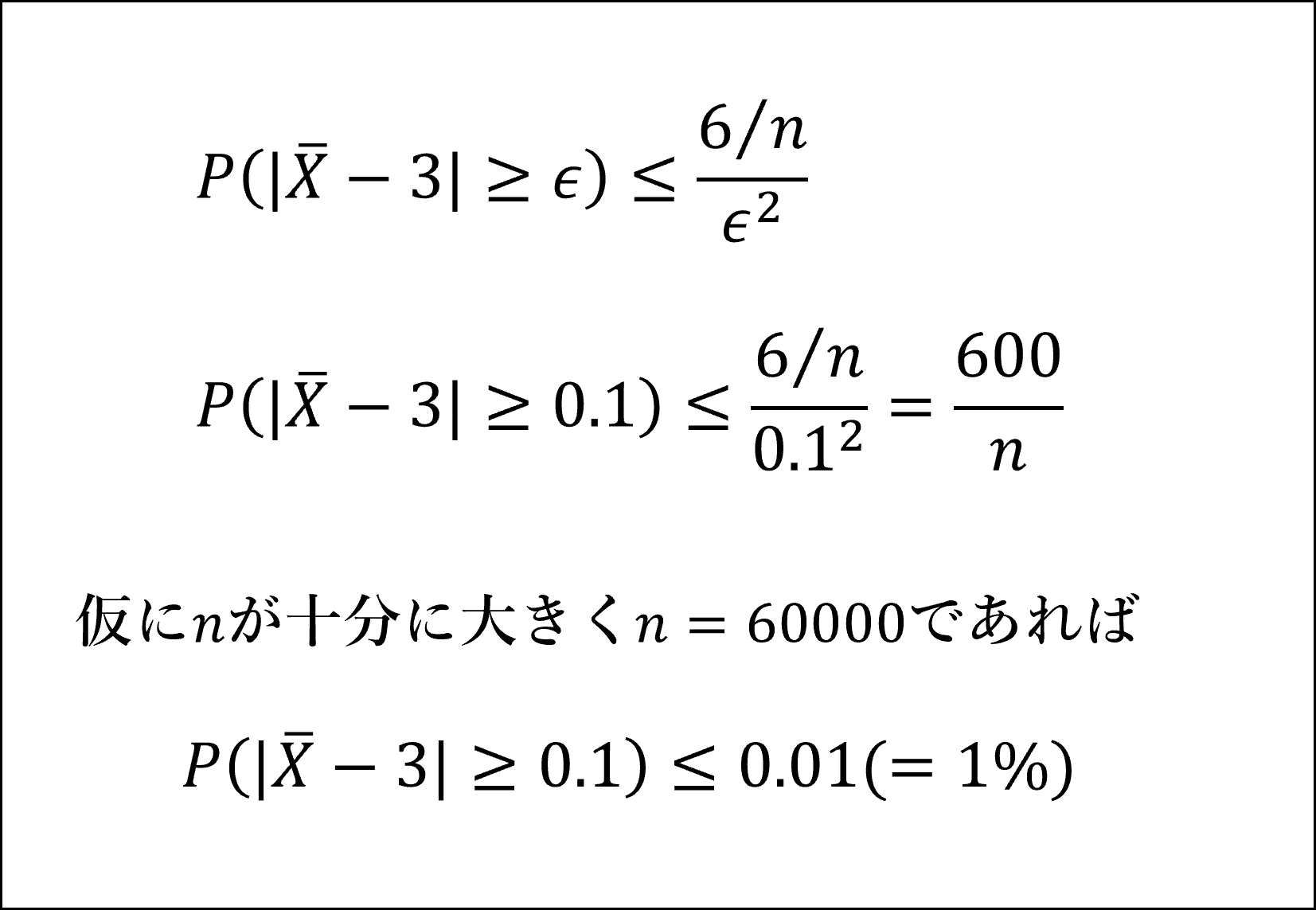
- これは「標本平均と期待値(=3)との差が0.1以上となる確率」が「1%以下」となることを意味しています。
(15番,16番以上)

