統計検定®2級過去問解説 2021年6月 問13～問22 [17番～35番]

※統計検定®は一般財団法人統計質保証推進協会の登録商標です（名称使用の許諾を受けています）。また、本記事は統計検定主催社側から公認されたものではございません。

※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。

問13 [17番]（2021年6月試験）

テーマ

• 一致推定量
• 不偏推定量

正答

選択肢①

解答例

　推定量とは母集団の母数（母平均、母分散など）を推定するために標本から計算される統計量（標本統計量）になります。例えば標本平均は母平均の推定量ですし、標本分散や不偏分散は母分散の推定量になります。

Ⅰ：正しいです。推定量（標本平均や標本分散、不偏分散など）はさまざまな値を取り得ますので「変数」になります。また、推定量が実際にどのような値になるかは確率的に決まりますので、推定量は「確率変数（変数のとりうる値についての確率が存在する変数）」になります。

Ⅱ：正しいです。推定量が母数に確率収束する（＝サンプルサイズnが極めて大きいときに推定量が母数に一致する）性質を推定量の一致性と呼びます。

Ⅲ：誤りです。推定量の期待値が母数に一致する性質を不偏性と呼び、不偏性をもつ推定量を不偏推定量と呼びます。一致性はサンプルサイズnが極めて大きいときの性質であるのに対して、不偏性はサンプルサイズnに関係しない「期待値」に関する性質になります。

　例えば、母分散の推定量として標本分散（nで割る）と不偏分散（n－1で割る）がありますが、両者ともに一致性を有します（サンプルサイズnが極めて大きいとき、標本分散も不偏分散も母分散に近似します）が、標本分散は不偏性を有しません。

　したがって、一推定量であれば必ず不偏推定量というわけではありません。

補足

• Ⅱはさりげなく問12の大数の法則にからめた問題で、問13を解きながら問12の考え方をひらめかせるような出題者側の意図も感じます。問13を解きながら「問12は確率収束（大数の法則）の話か！」と気づいた受験生も少なくなかったかもしれません。

（17番、以上）

問14 [18番]（2021年6月試験）

テーマ

• 不偏推定量
• 母平均μのさまざまな推定量

正答

選択肢⑤

解答例

　母平均μの推定量といえば標本平均ですが、母平均μの推定量として標本平均以外の推定量も考えてみよう、という問題です。

　具体的には、1つ目は「標本平均」、2つ目は「1番目とn番目の平均」、3つ目は「1番目の値（そのもの）」、4つ目は「各番目の値Xiと各番号iの積の和に2/{n(n+1)}を掛けた値」になります。

　これら4つの推定量はすべてその期待値が母平均μに一致しますので、すべて母平均μの不偏推定量になります。具体的には以下のように確認できます。

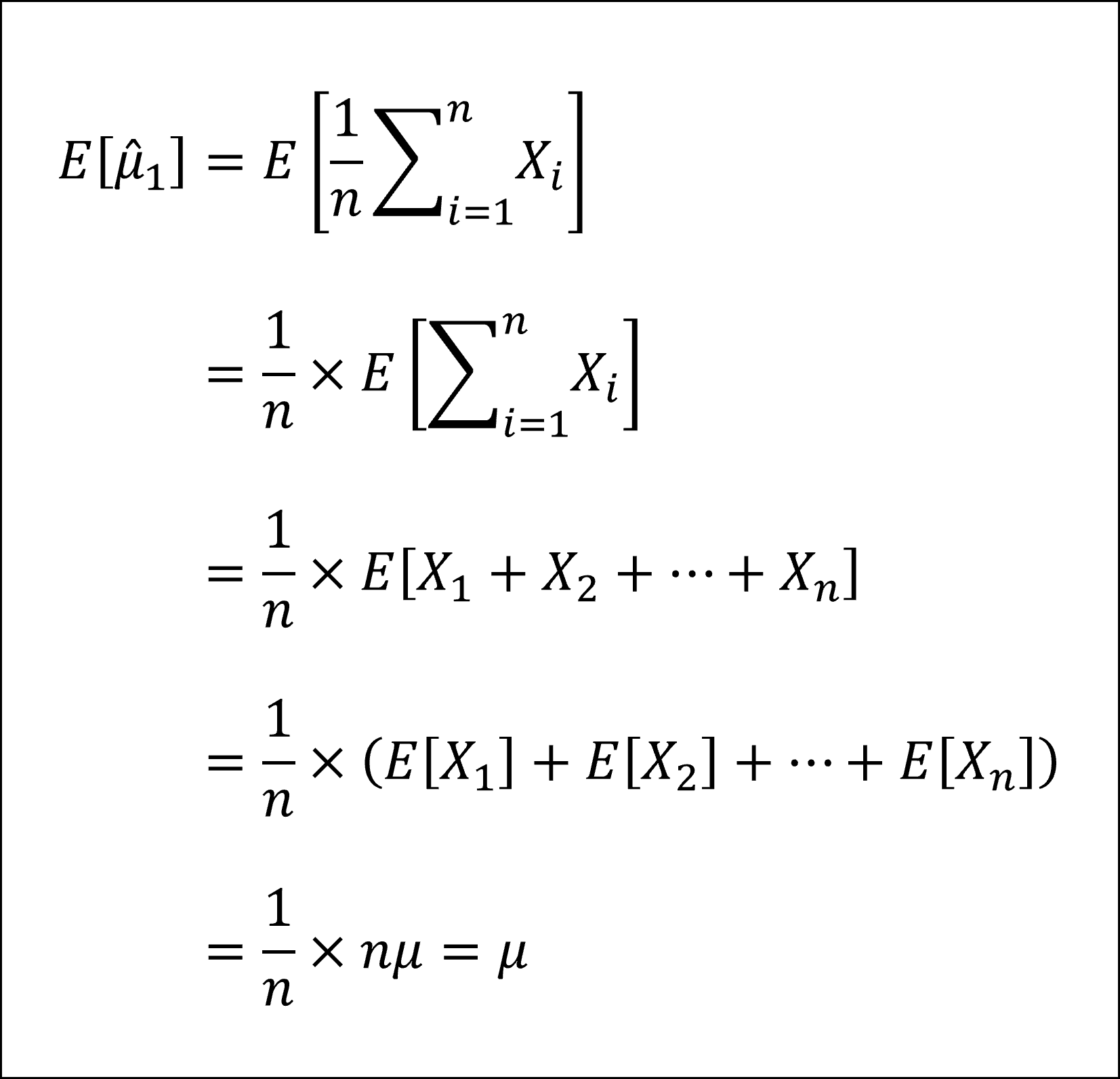
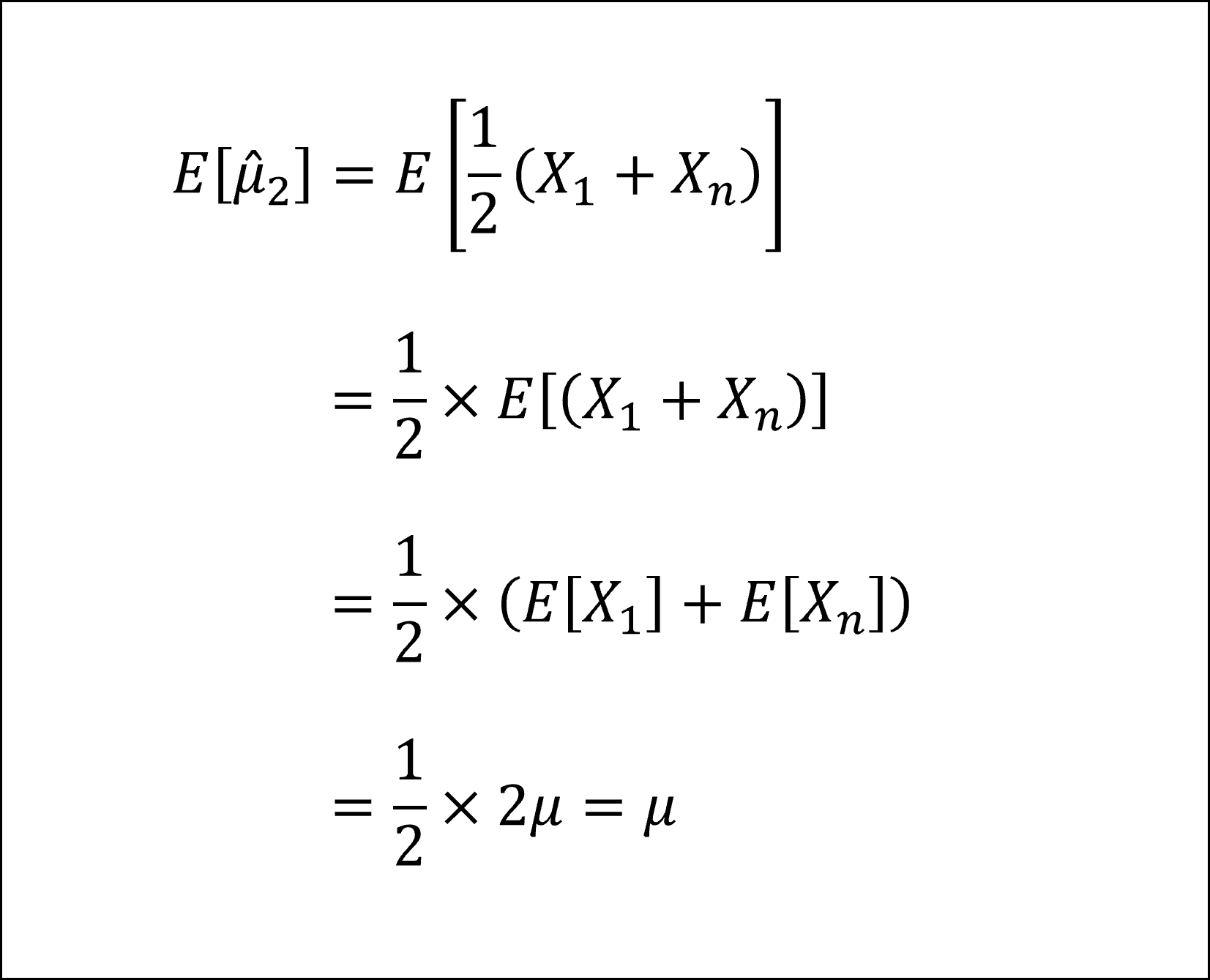
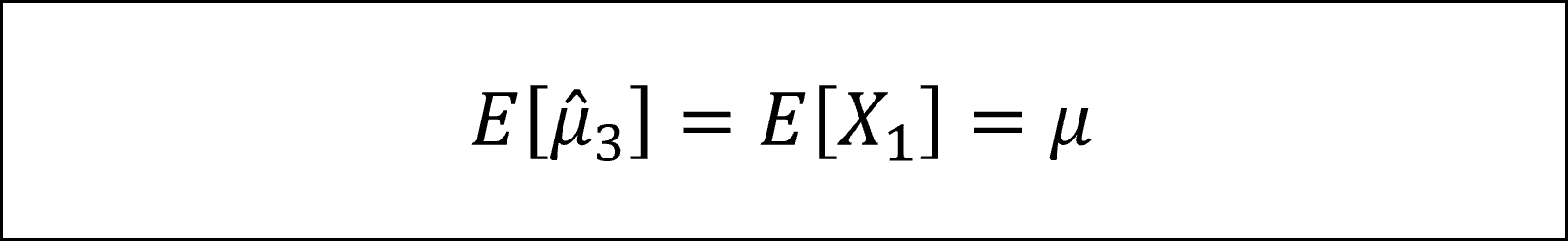
　※4つ目の推定量の計算においては「等差数列の和の公式」を用いています。

補足

• μという記号の上部に付された[^]の記号は「ハット」と呼び、統計学では[^]が付された記号は多くの場合「推定量」をあらわします。
• 等差数列の和の公式の記憶があいまいで、4つ目の推定量の期待値を計算できなかった人も多いかもしれません。項数×(初項+末項)＝n(n+1)のかたちを見慣れておきましょう。

（18番、以上）

問14 [19番]（2021年6月試験）

テーマ

• 分散の計算
• 分散の性質

正答

選択肢①

解答例

　4つの推定量の分散は以下のように計算できます。

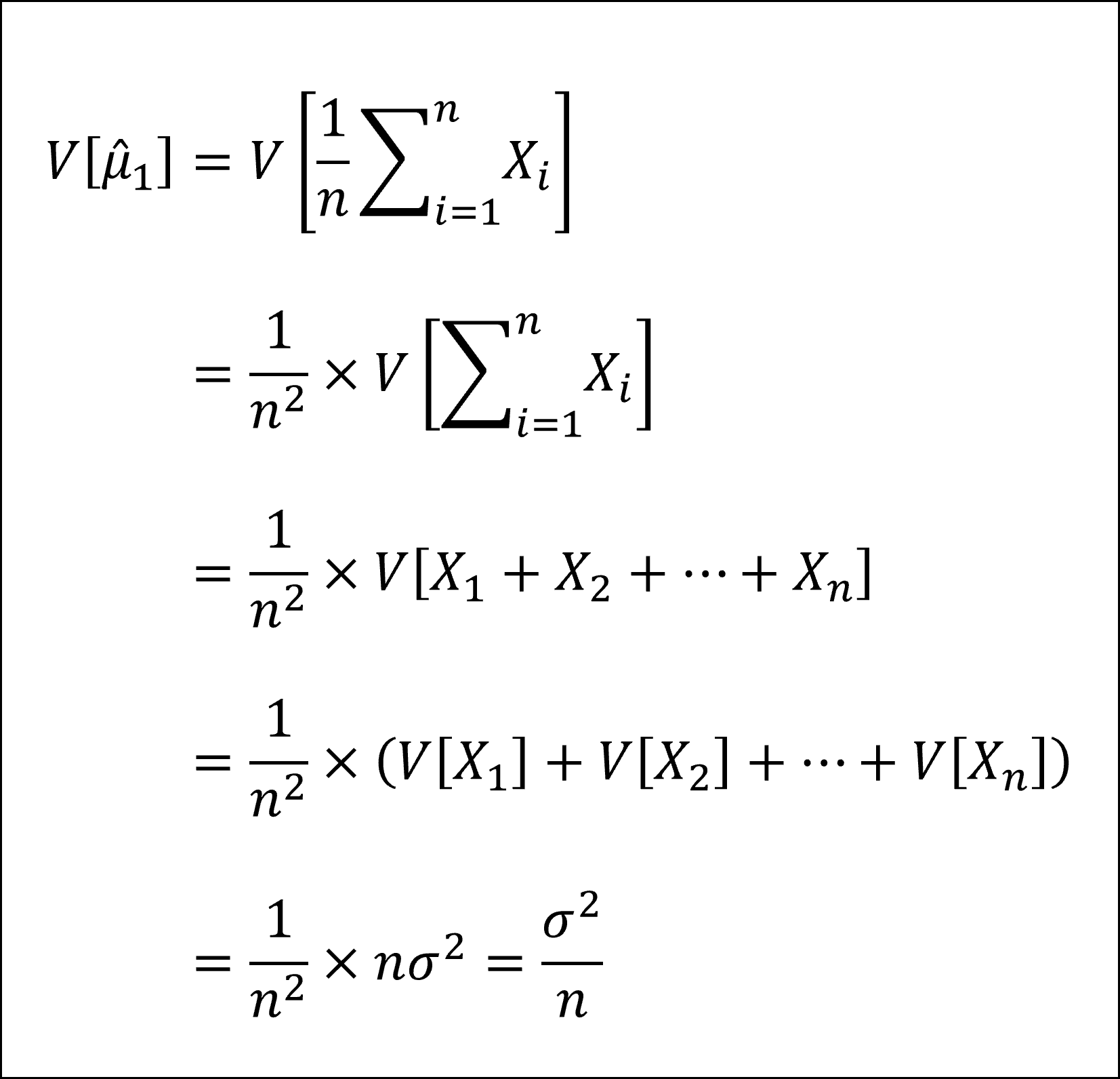
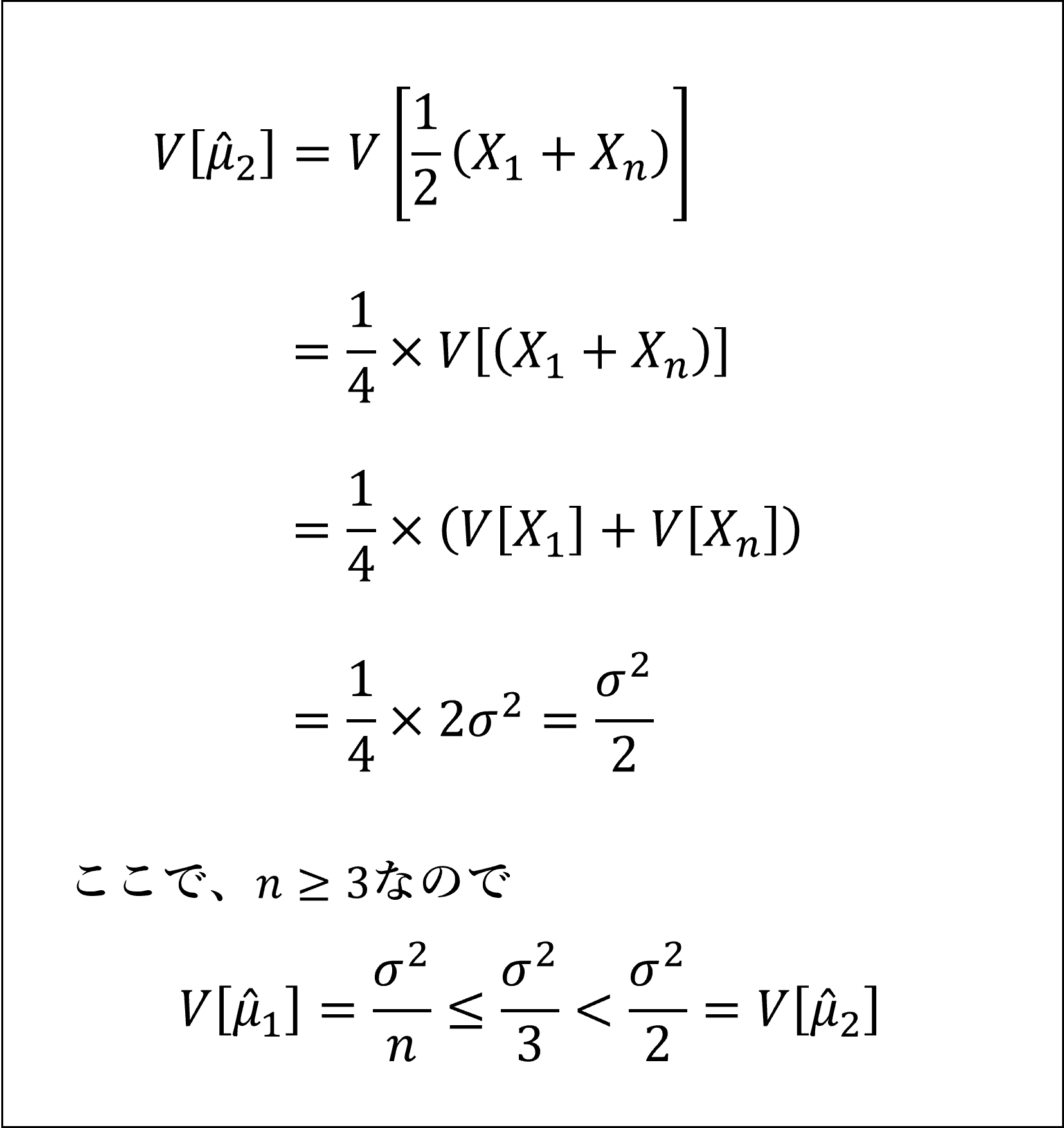
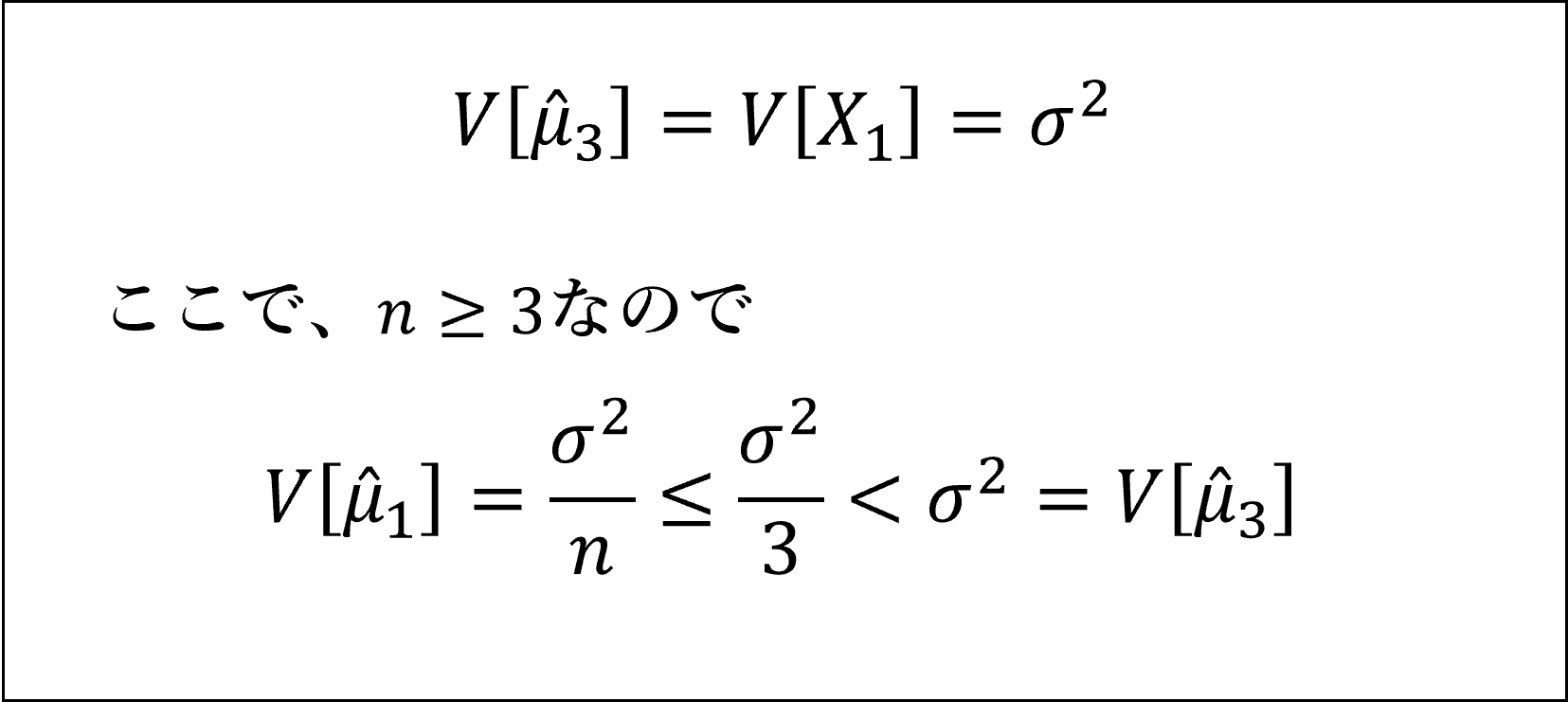
　上記のとおり、1つ目の推定量の分散が最も小さくなります。

　※4つ目の推定量の計算においては「自然数の2乗の和の公式」を用いています。

補足

仮に1つ目の推定量（＝標本平均）よりも4つ目の推定量の方が分散が小さかったとします。そうすると、標本平均よりも4つ目の推定量の方が母平均μの推定量として良い（分散が小さく精度の高い）推定量となってしまいます。そんなはずもないだろう、ということで選択肢➀を選ぶこともできそうです。

（19番、以上）

問15 [20番,21番]（2021年6月試験）

テーマ

• 標本平均の性質
• 標準正規分布の付表の読み取り

正答

[20]選択肢④　[21]選択肢③

解答例

　問題文より母集団は母平均μ、母分散12^2の正規分布N(μ, 12^2)にしたがいますので、この母集団から抽出した標本をXとおくと

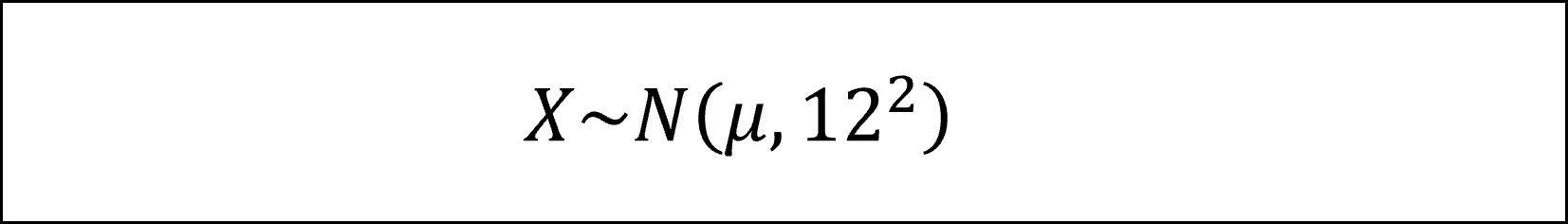
[20番]したがって、この母集団から抽出した標本の平均（標本平均）は、標本平均の性質より

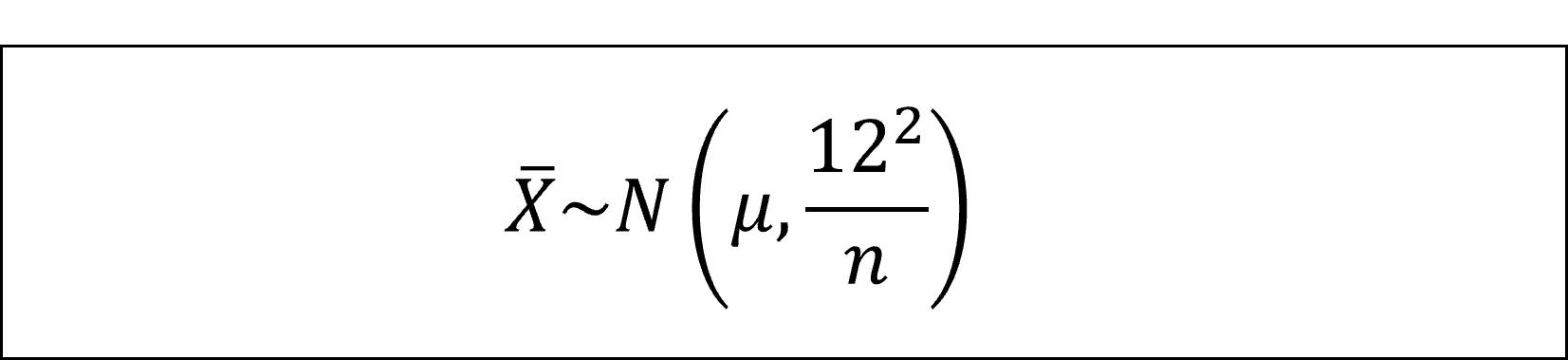
となります。さらに、標準正規分布にしたがうように整理すると

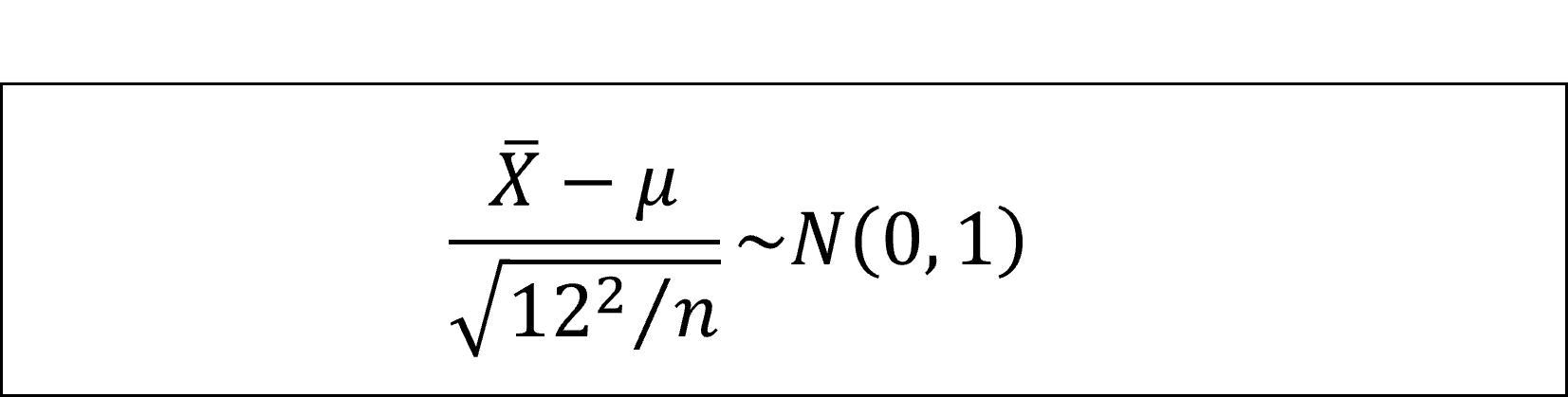
となります。標準正規分布の付表から上側2.5%点を読み取るとz=1.96ですので、母平均μの95%信頼区間は以下のように整理できます。

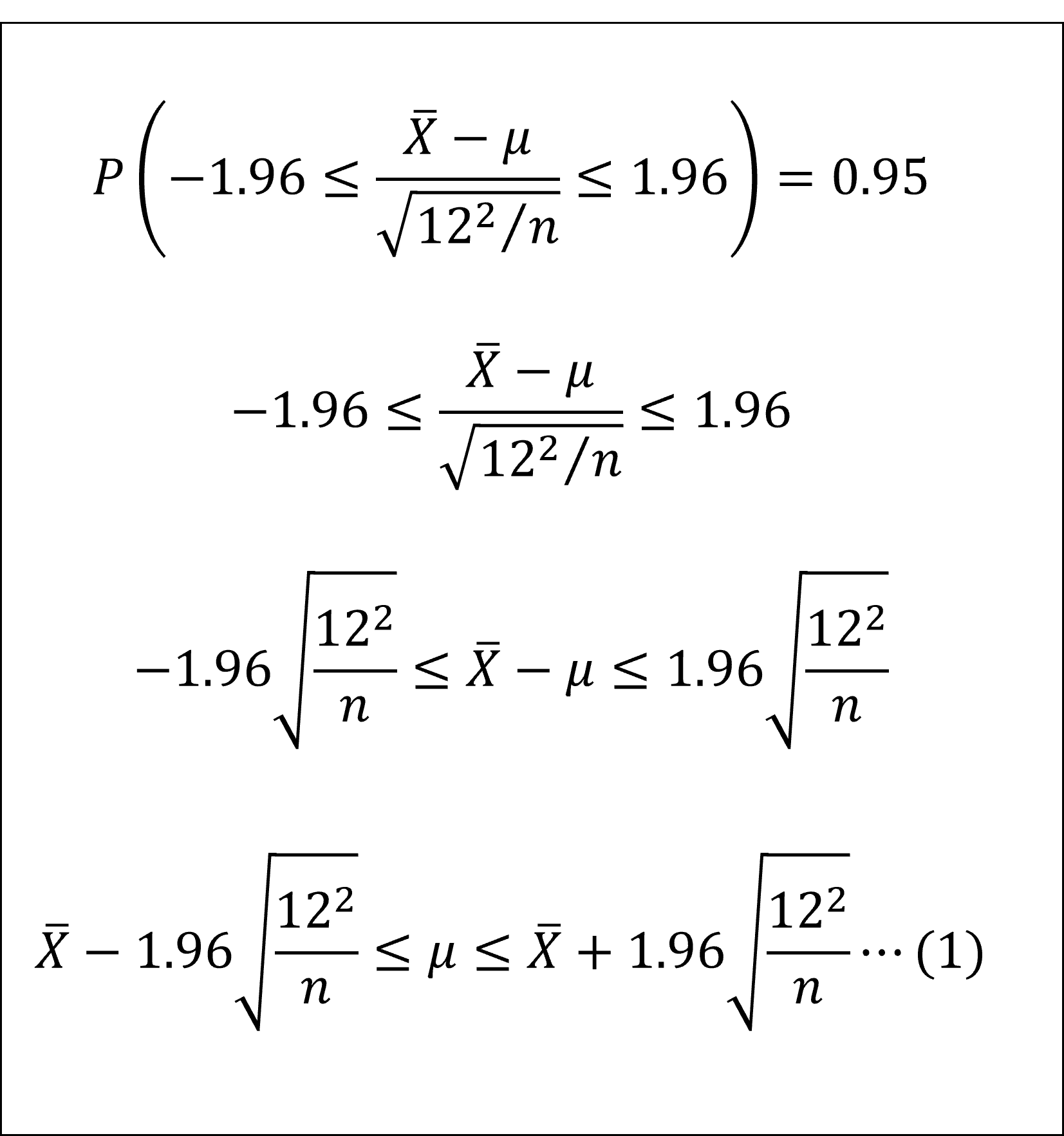
ここで、問題文より、サンプルサイズn=100で、観測された標本平均は5.25ですので、これを(1)式に代入し、以下のように95%信頼区間が求まります。

[21]95%信頼区間の(1)式の右辺の値と左辺の値の差が4以下となればよいので、以下のように整理できます。

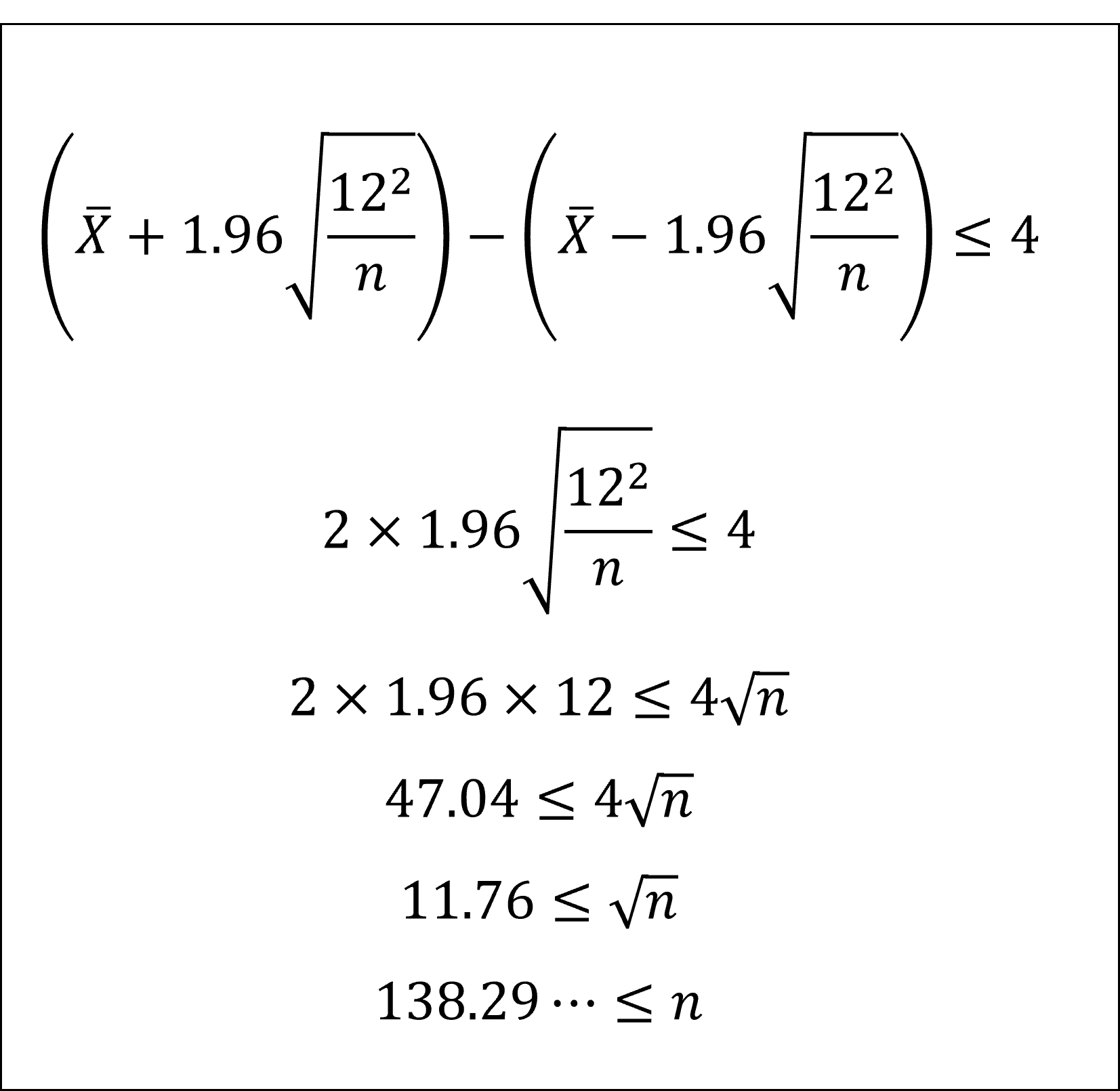
以上より、nが最低限139あれば95%信頼区間の幅が4以下となります。

補足

• [20番]は非常にオーソドックスな問題で絶対に落としたくない問題です。
• [21番]も(1)式をしっかり整理できていれば問題なく解けそうです（逆に言うと(1)式の整理ができなければ少々混乱してしまうかもしれません）。

（20番21番、以上）

問16 [22番]（2021年6月試験）

テーマ

• 定数項のない単回帰モデル
• 残差平方和
• 最小二乗法

正答

選択肢①

解答例

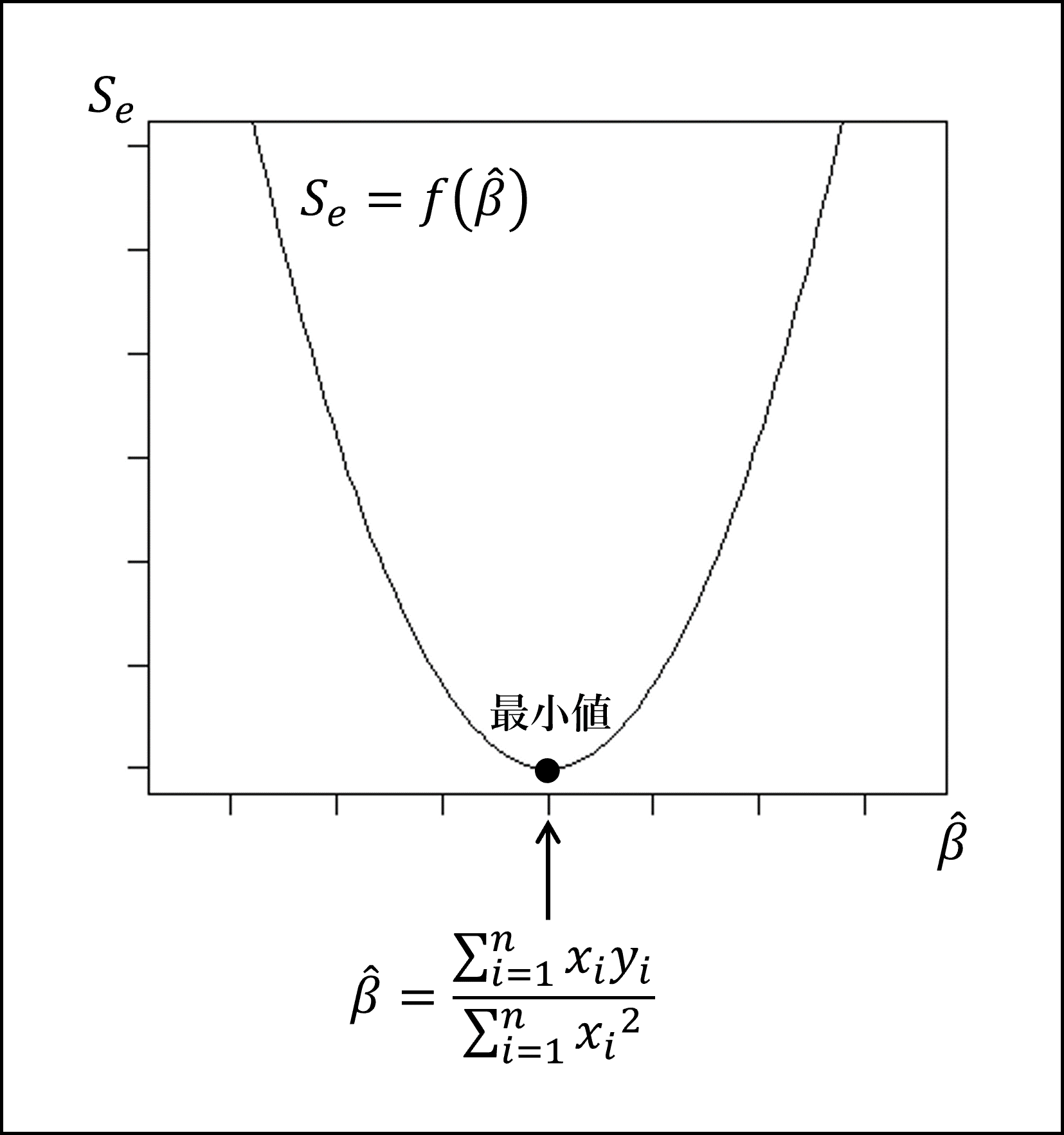
　定数項を含まない単回帰モデルということに注意が必要です。

　パラメータβの最小二乗推定量、つまり、最小二乗法によって残差平方和が最小になるときのパラメータβの推定量は以下のように整理できます。

補足

• 「定数項を含まない」という点がポイントです。
• モデルのパラメータを最小二乗法で推定する流れを理解しているかが問われます。
• 上記は微分した式を0とおいて解答しましたが、残差平方和の式をβについての二次方程式として整理し、頂点（最小値）となる点を求める方法でも解を導けます。

※参考図

（22番、以上）

問16 [23番]（2021年6月試験）

テーマ

• 定数項のない単回帰モデル
• 残差
• Σの計算

正答

選択肢②

解答例

　定数項を含まない単回帰モデルをまず図でイメージしておきましょう。

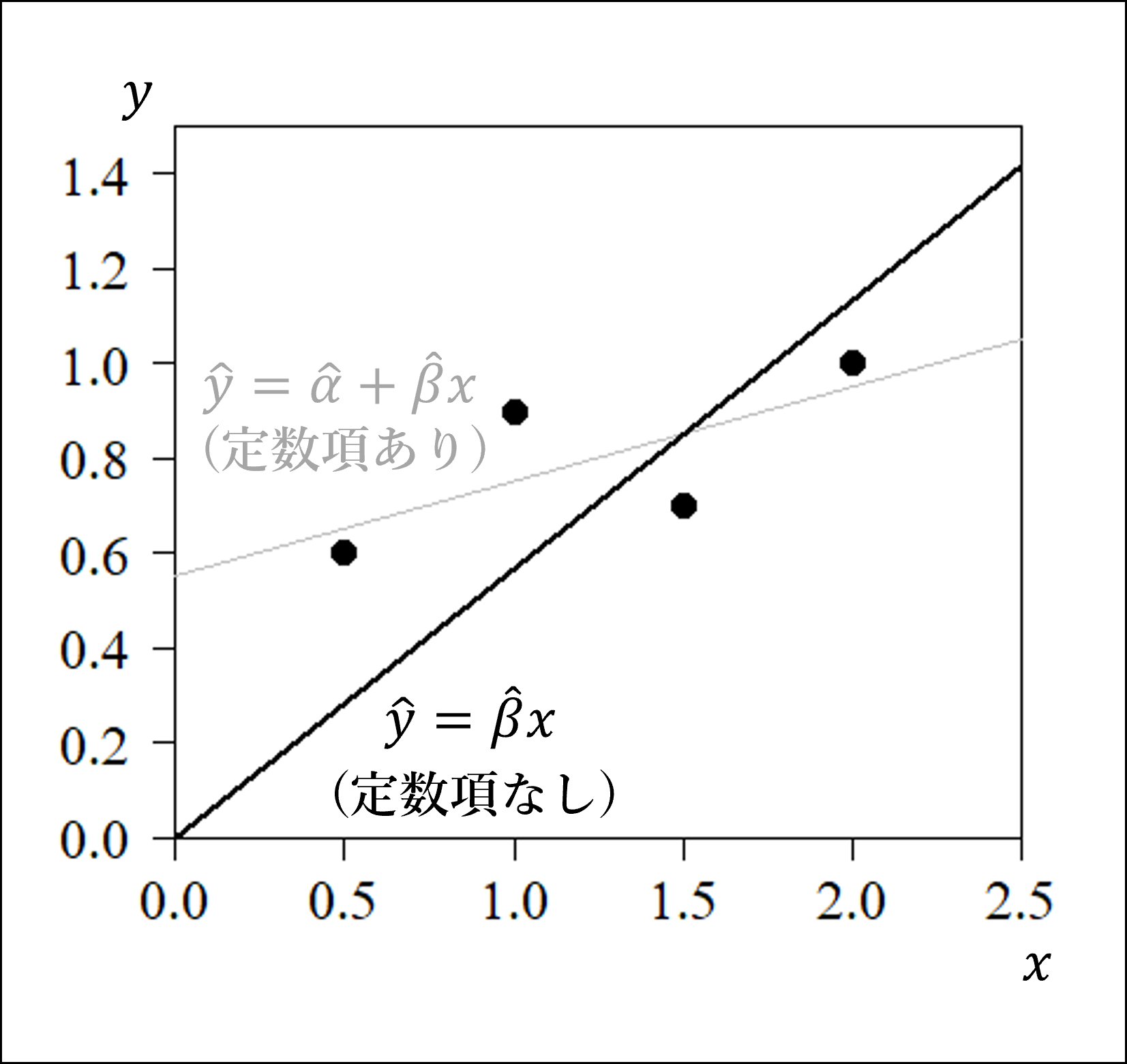
　よく見慣れた「定数項を含む単回帰モデル」は灰色の線で、今回のテーマである「定数項を含まない単回帰モデル」は黒色の線で描画しています。

　図からわかるように、定数項を含まない単回帰モデルは必ず原点(0,0)を通り、各プロット（観測値）との距離に偏りが生じる（x＝0に近いほど直線と観測値との距離が大きい傾向など）という性質があります。

　これを踏まえて問題文の各記述の内容を確認していきましょう。

＜記述Ⅰについて＞

※参考：前問[22]で求めたパラメータβの推定量は以下の通りです

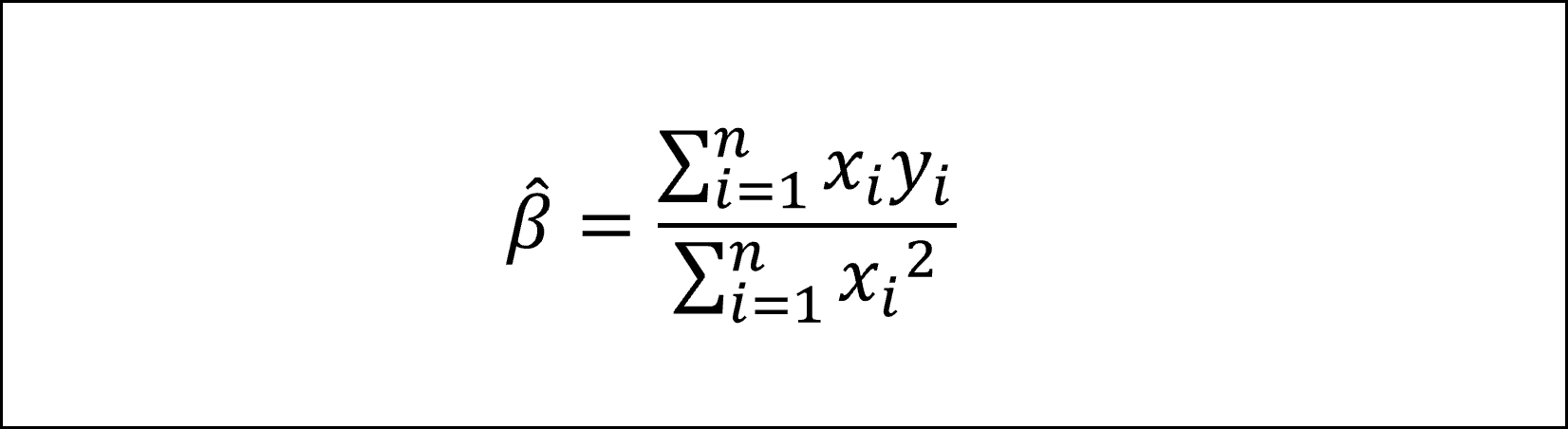
（上記の導出は前問[22]の解答例をご覧ください）

＜記述Ⅱについて＞

＜記述Ⅲについて＞

＜記述Ⅳについて＞

補足

• 本問はモデルの仮定からパラメータの推定までの流れの理解を総合的に問う良問であり難問です。
• とはいえ、各記述の式をシンプルに整理していくと、回帰係数βの式に整理できることに気づけるかと思います。あとは前問[22番]で導いたβの式と矛盾がないかを確認すれば正答できそうです。
• 逆に言うと[22番]の問題が解答できていないと、本問で正答することは難しそうです。
• なお、記述Ⅰ～Ⅳはいずれも定数項を含む単回帰モデルでは常に成り立ちます。

（23番、以上）

問17 [24番]（2021年6月試験）

テーマ

• 母比率の区間推定
• 二項分布
• 中心極限定理
• 標準正規分布の付表

正答

選択肢②

解答例

　表が出る回数を𝑥とおくと、𝑥は試行回数𝑛、成功確率（表が出る確率）𝑝の二項分布𝐵(𝑛, 𝑝)にしたがい、期待値は𝑛𝑝、分散は𝑛𝑝(1−𝑝)となります。また、𝑛=500と試行回数𝑛が十分大きいことから中心極限定理により𝑥は正規分布にしたがいますので、

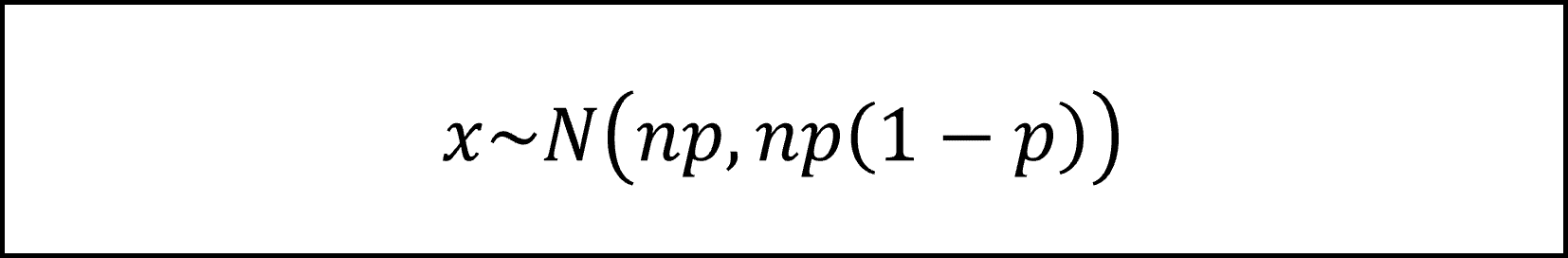
となります。ここで、上記の𝑥を𝑛で割った値、つまり、標本比率のかたちに整理すると

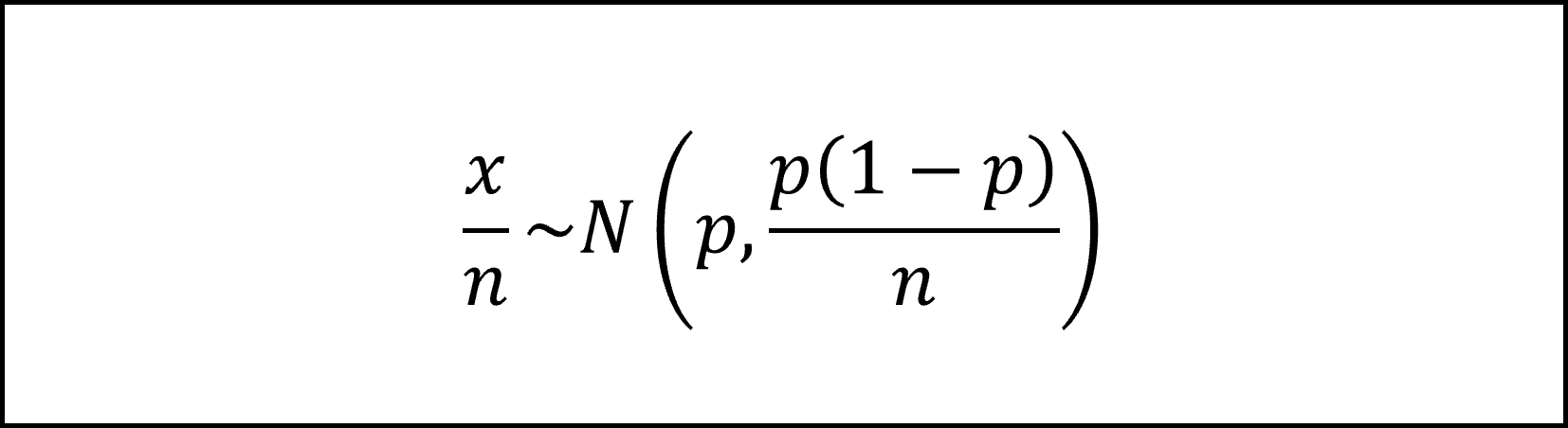
となります。これを標準化した（平均を引いて標準偏差で割った）値は標準正規分布𝑁(0,1)にしたがいますので、

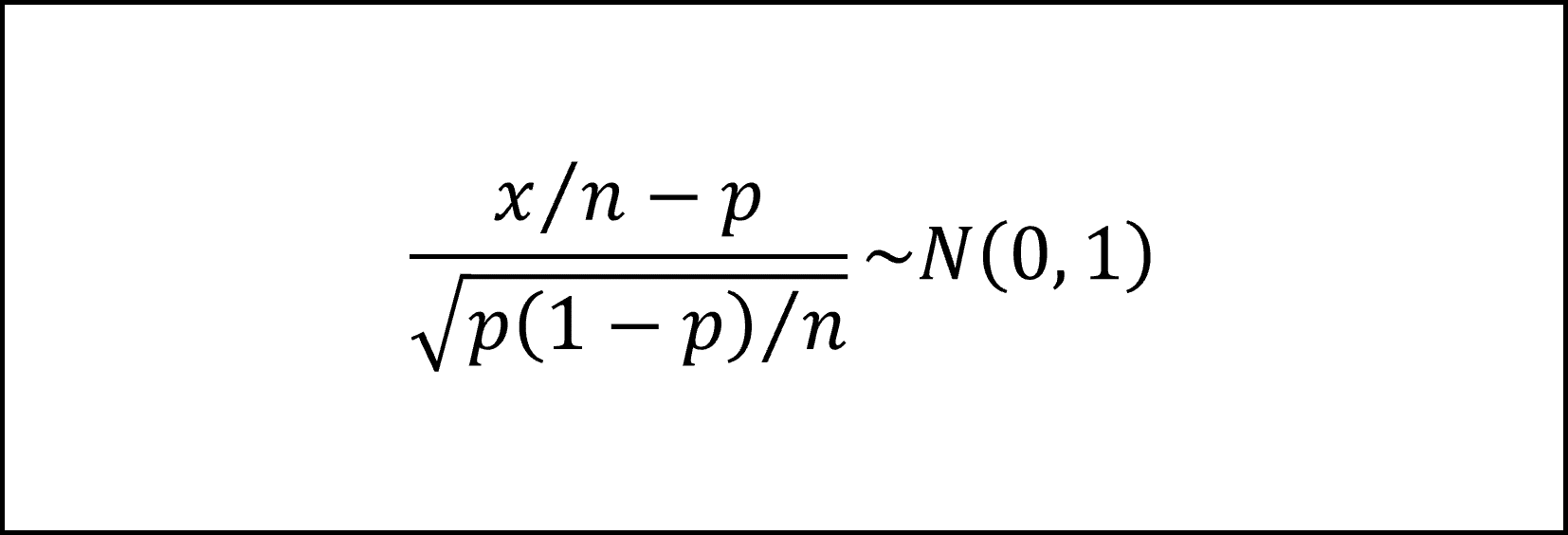
となります。

　付表1から標準正規分布の下側2.5%点が−1.96で、上側2.5%点が1.96ですので、以下のように整理できます。

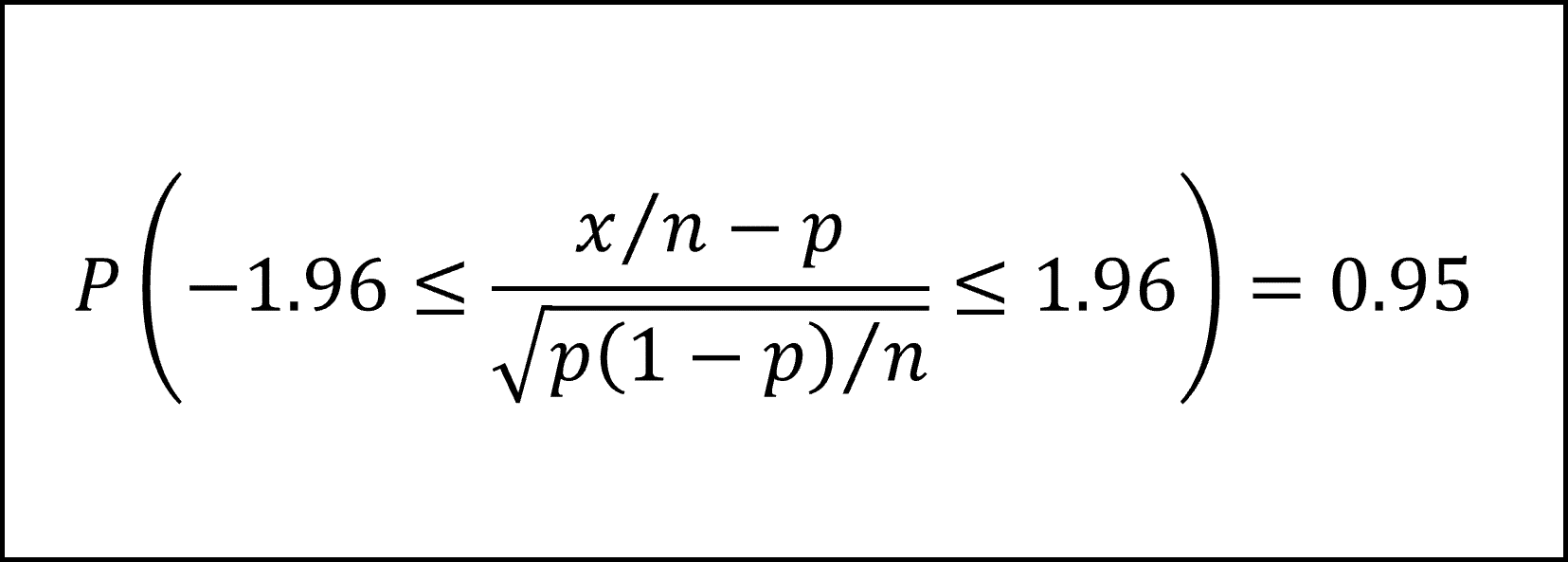
　最後に、試行回数𝑛=500、成功回数𝑥=284を代入し、表が出る確率𝑝の95%信頼区間を以下のように整理できます。

　ここで不等式の左辺と右辺において、近似計算法により表が出る確率𝑝に標本比率𝑥/𝑛＝284/500＝0.568を代入して、

補足

　母比率の区間推定は少数点以下の計算や平方根の計算のために計算が煩雑になりがちです。したがって、式をしっかりと整理してから電卓での計算を行うことをおすすめします。

（24番、以上）

問17 [25番]（2021年6月試験）

テーマ

• 二項分布
• 棄却域
• P-値（≠有意水準α）
• 離散変数の仮説検定

正答

選択肢①

解答例

　空欄(ア)には表が出た回数Xが4回となる確率が入ります。Xは𝑛＝8、𝑝＝1/2の二項分布B(8,1/2)にしたがいますので、二項分布の確率関数を用いて以下のように計算できます。

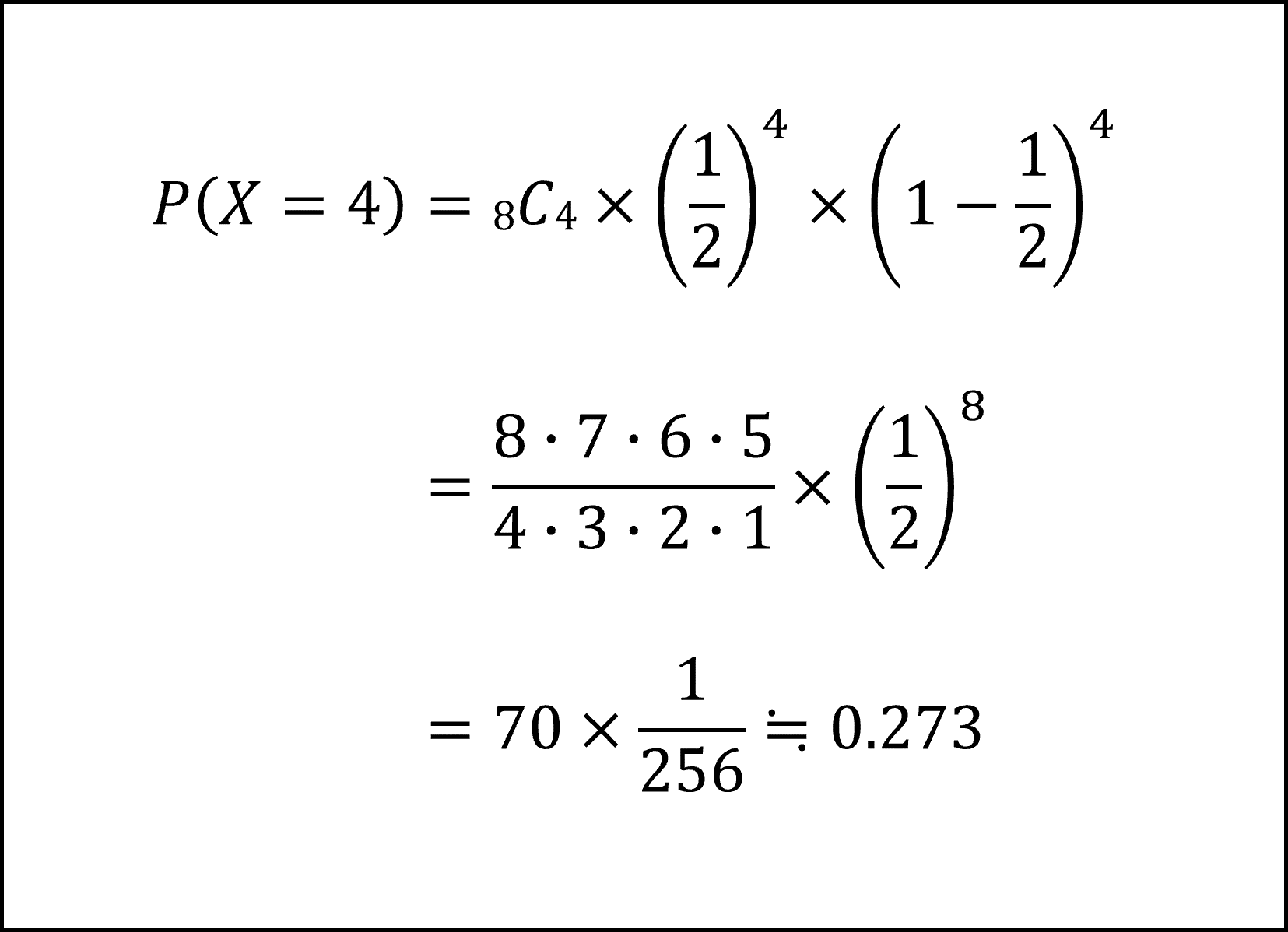
　空欄(イ)は「X＝7のときのP-値」、すなわち、「X＝7以上となる確率」が入りますので、問題文に与えられた確率分布の表より

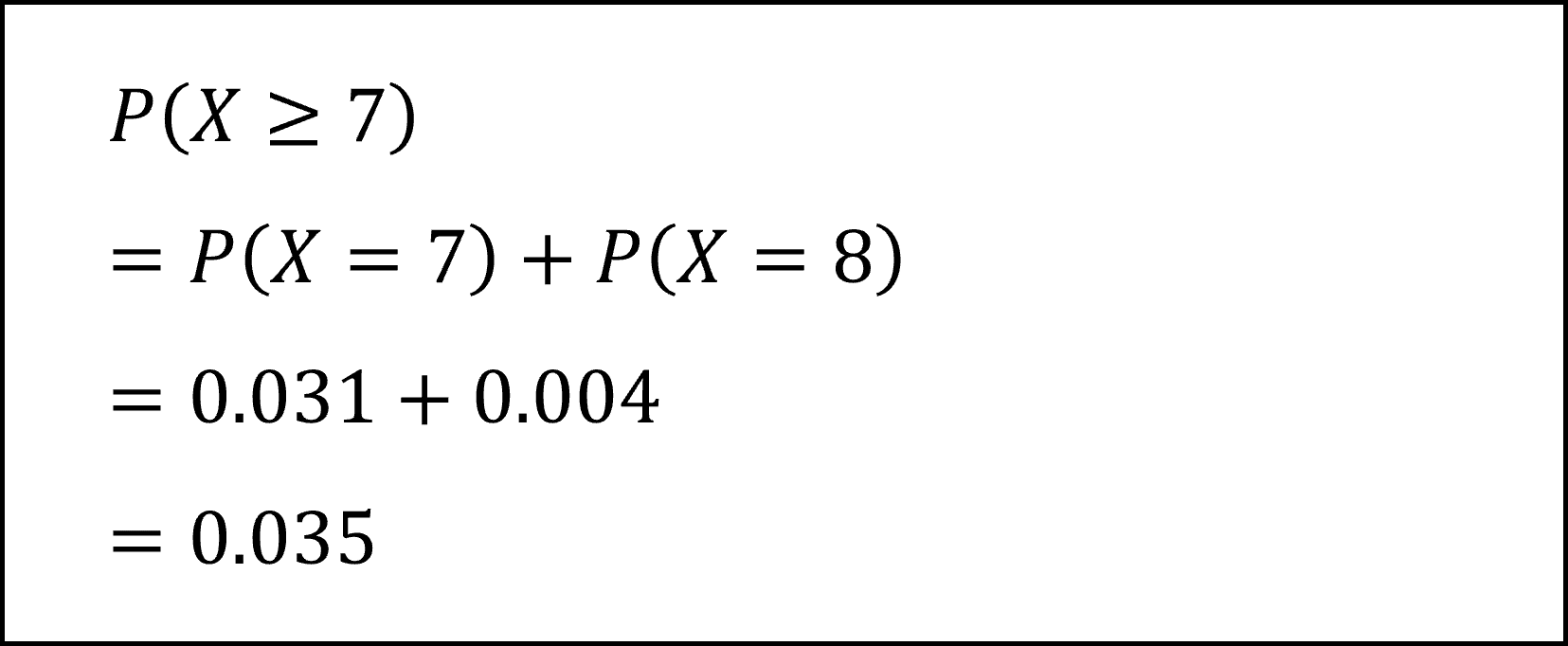
となります（対立仮説が上側のみに設定された片側検定ですので、Xが7以上の確率のみを計算している点に注意しましょう）。

　次に、後半の文章については、「Xと4との差が定数c以上となるときに帰無仮説を棄却する両側検定」を前提としています（例えばc=3であれば「Xと4との差が3以上となるX=0,1,7,8のときに帰無仮説を棄却する」ということになります）。

　この前提のもと、空欄(ウ)には「X=7のときのP-値」、すなわち、「Xと4との差が3のときのP-値」が入ります。これは言い換えると「Xと4との差が3以上となる確率」ですので、問題文に与えられた確率分布の表より

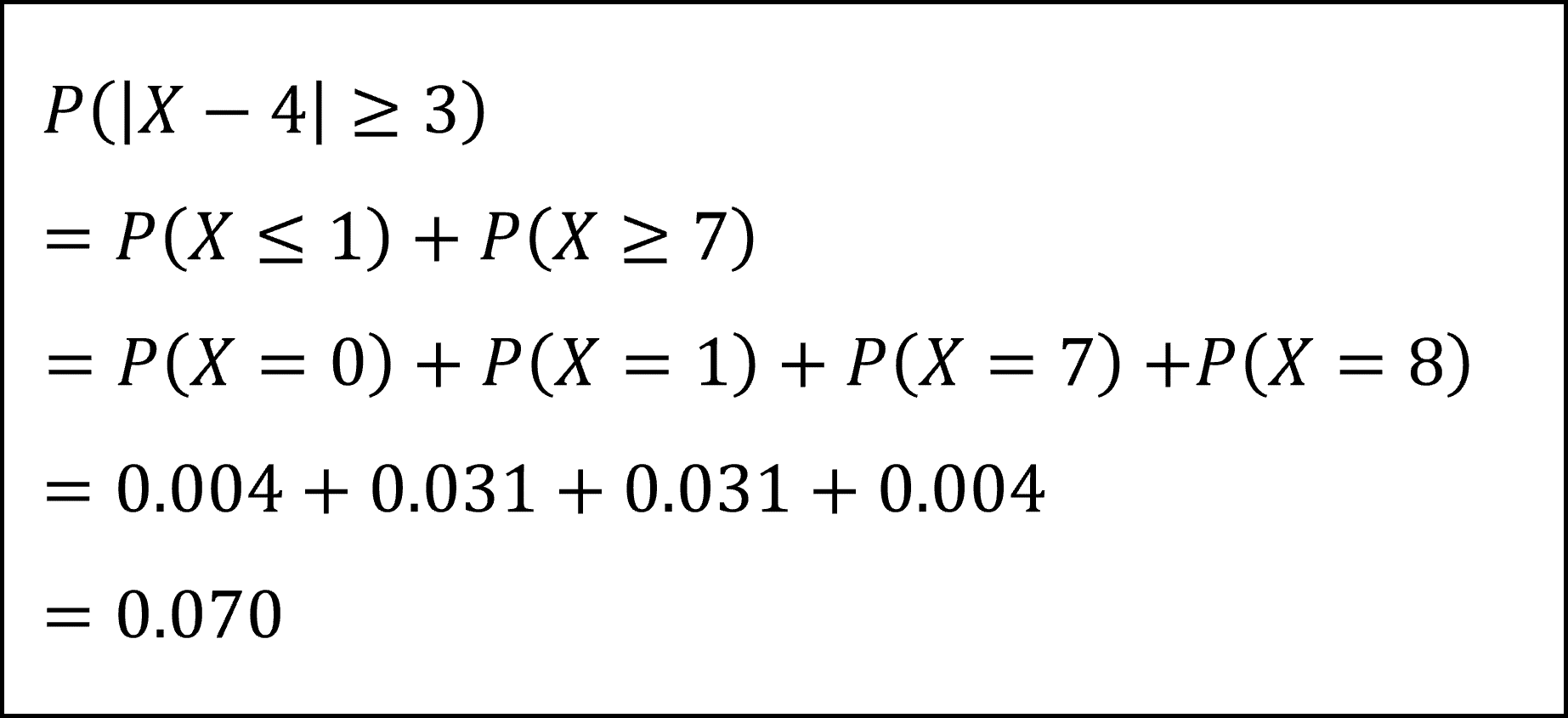
となります（対立仮説が上側と下側に設定された両側検定ですので、X≧7 だけでなく、X≤1 の確率も計算している点に注意しましょう。

補足

• 空欄(ウ)の絶対値の不等式が混乱を招きそうですが、言葉で表現すると「Xと4との差が一定以上となれば帰無仮説を棄却する」というだけの話で実はシンプルな問題になります。
• なお、定数cは棄却域のスタート地点を表し、定数c以上となる確率が有意水準になります。

（25番、以上）

問18 [26番]（2021年6月試験）

テーマ

• 標準正規分布
• カイ二乗分布
• t分布

正答

選択肢②

解答例

　2つの正規母集団が前提となっていますので、標本平均および標本平均の差がしたがう分布は以下のように整理できます。

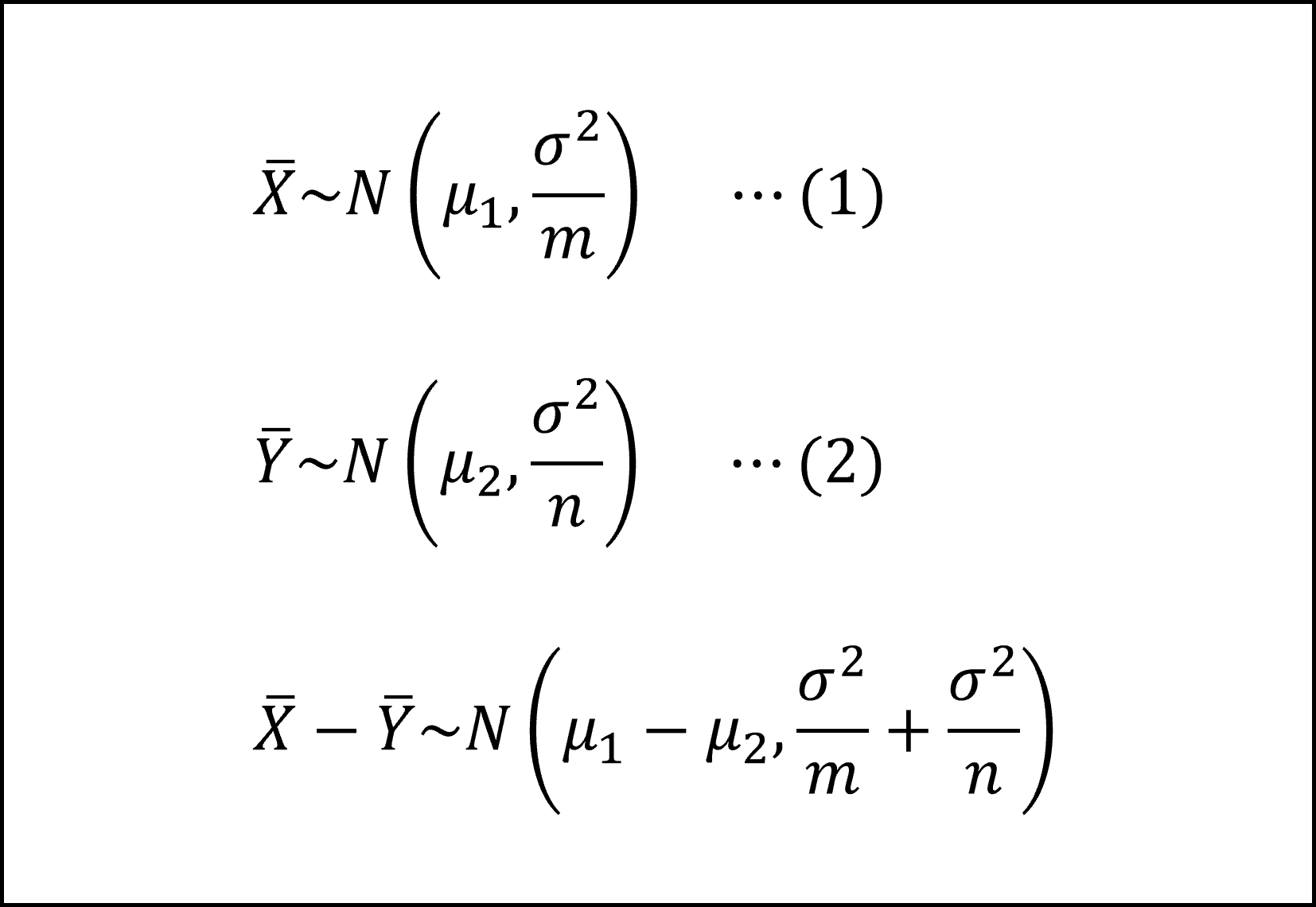
　したがって、標本平均の差を標準化した（平均を引いて標準偏差で割った）以下の【A】は標準正規分布N(0,1)にしたがいます。

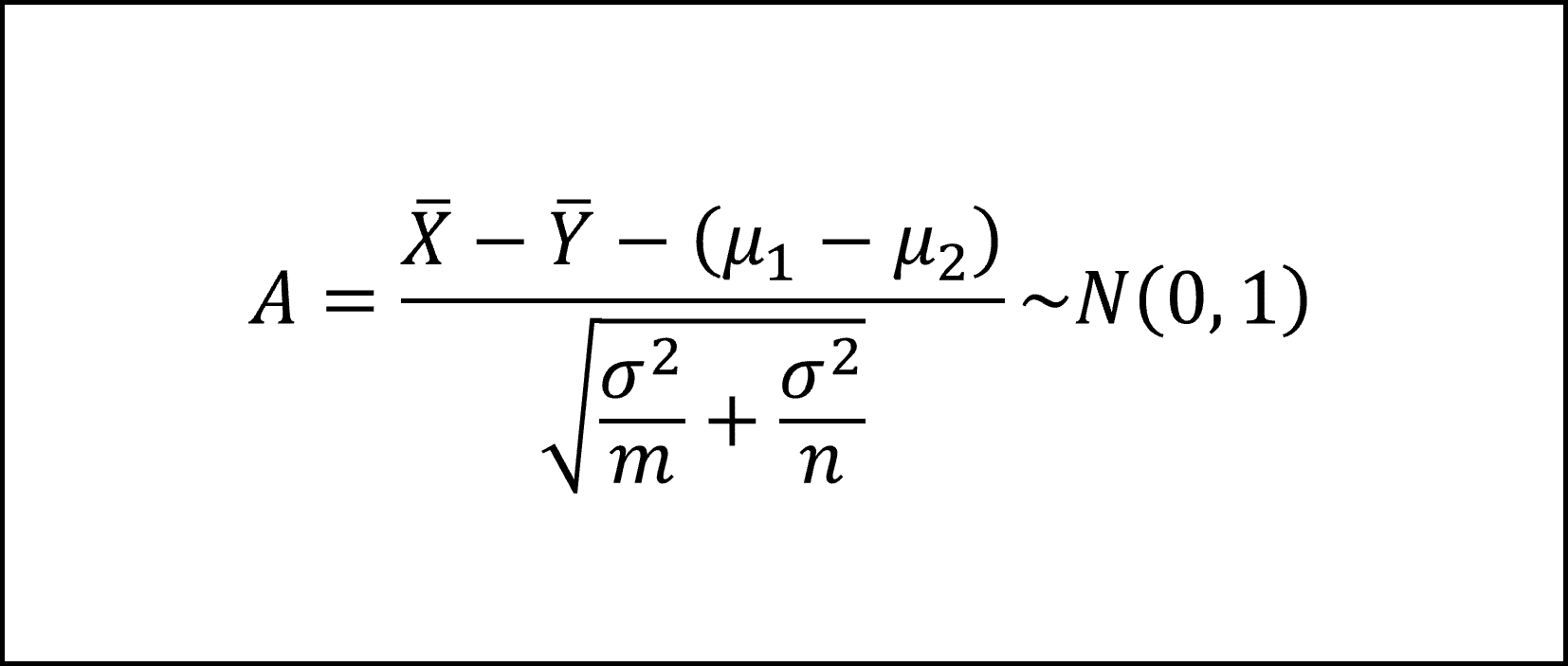
　また、2つの正規母集団が前提となっていますので、以下のように標本の各観測値は正規分布にしたがい、これを標準化すると（平均を引いて標準偏差で割ると）標準正規分布にしたがいます。

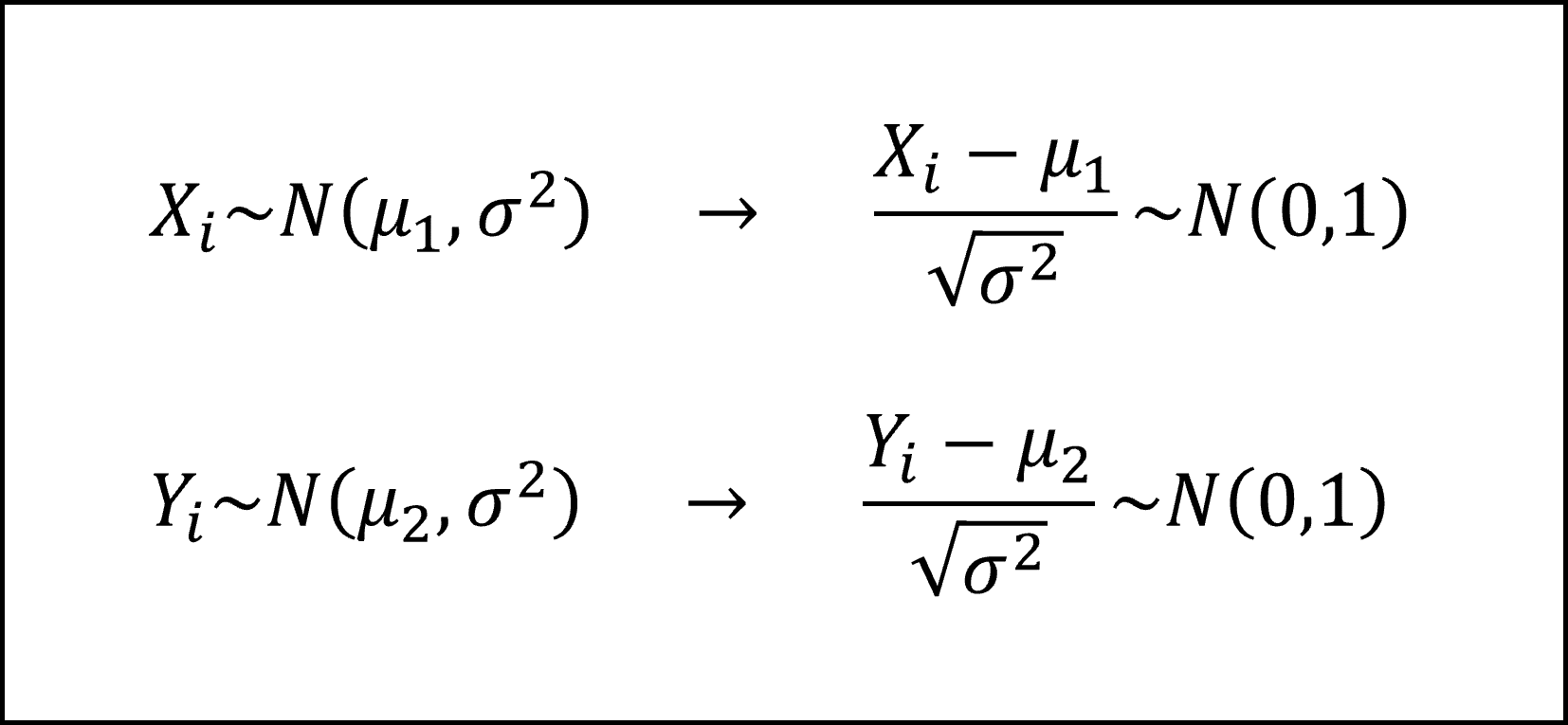
　標準正規分布にしたがう確率変数の二乗和（平方和）は、サンプルサイズを自由度とするカイ二乗分布にしたがいますので、以下のように整理できます。

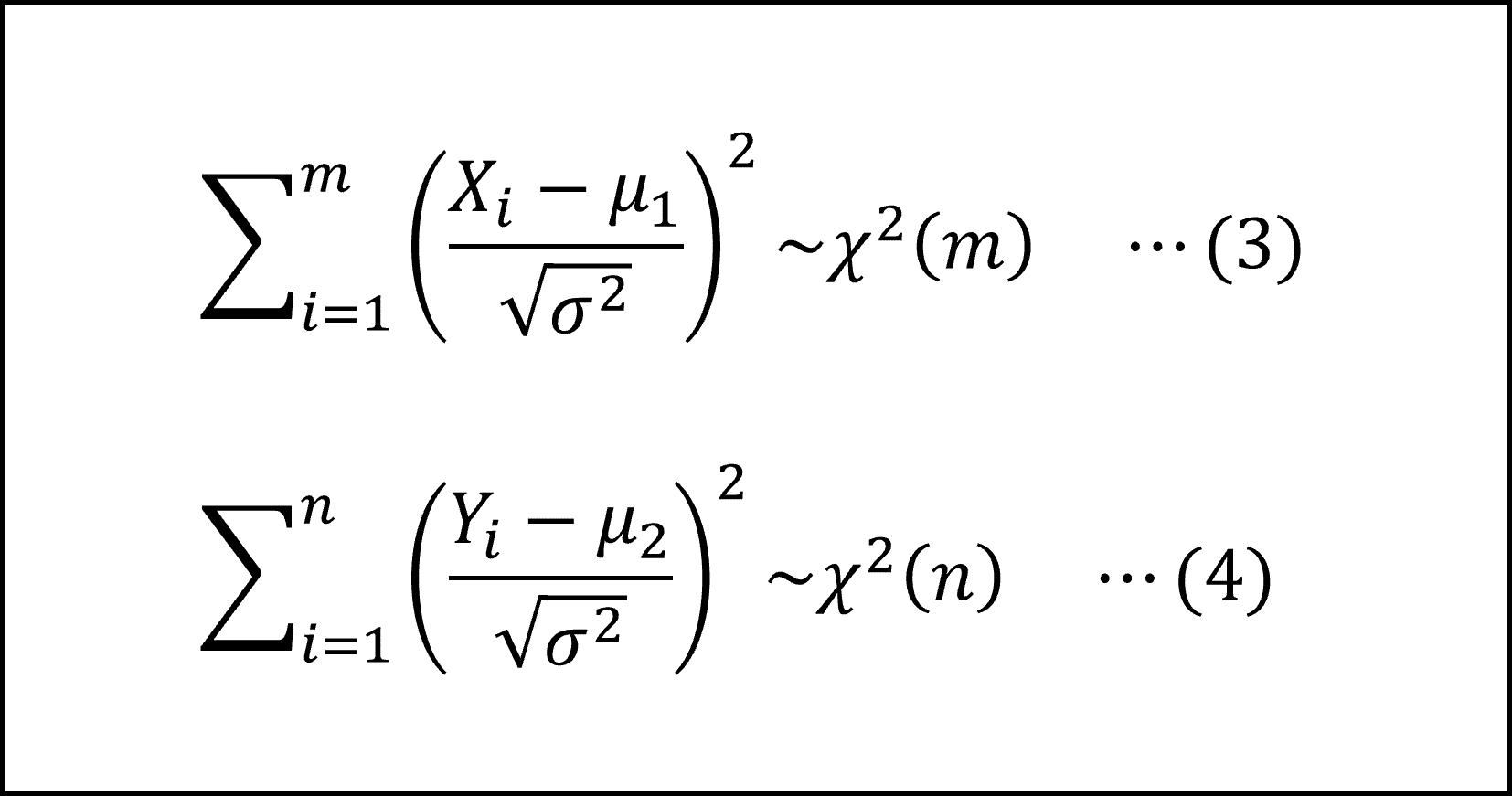
　ここで、上記の(3)式、(4)式を不偏分散を用いて整理した以下の式は、サンプルサイズから1を引いた値を自由度とするカイ二乗分布にしたがいますので、以下のように整理できます。

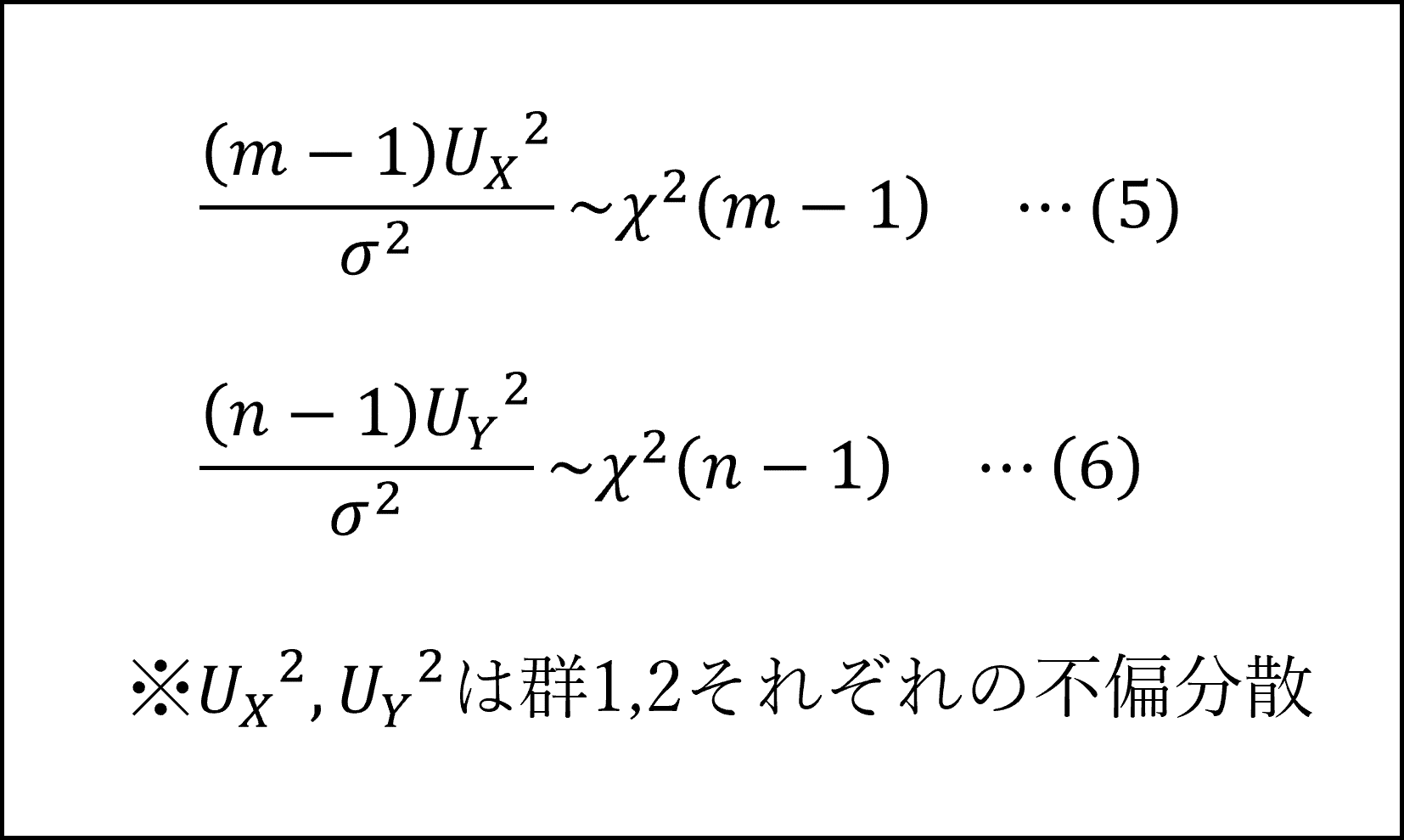
（※こちらの式の導出は別の記事にてご紹介します：）

となります。そして(5)式、(6)式、および、カイ二乗分布の再生性より、【B】は以下のように整理されます。

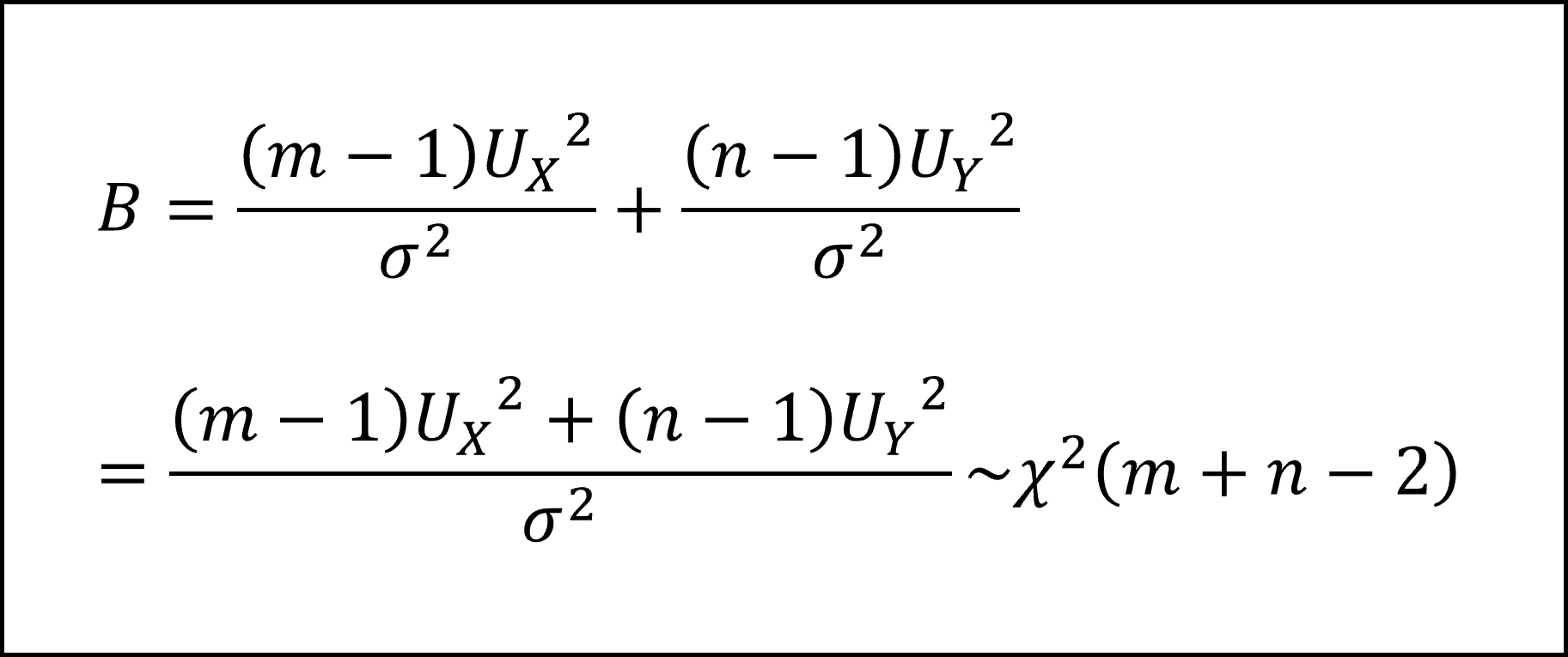
　また、t分布は「標準正規分布にしたがう確率変数Z」を「カイ二乗分布にしたがう確率変数を自由度で割った値の平方根」で割って計算される確率変数がしたがう分布ですので、自由度m＋n－2のt分布にしたがう検定統計量【T】は以下のように整理できます。

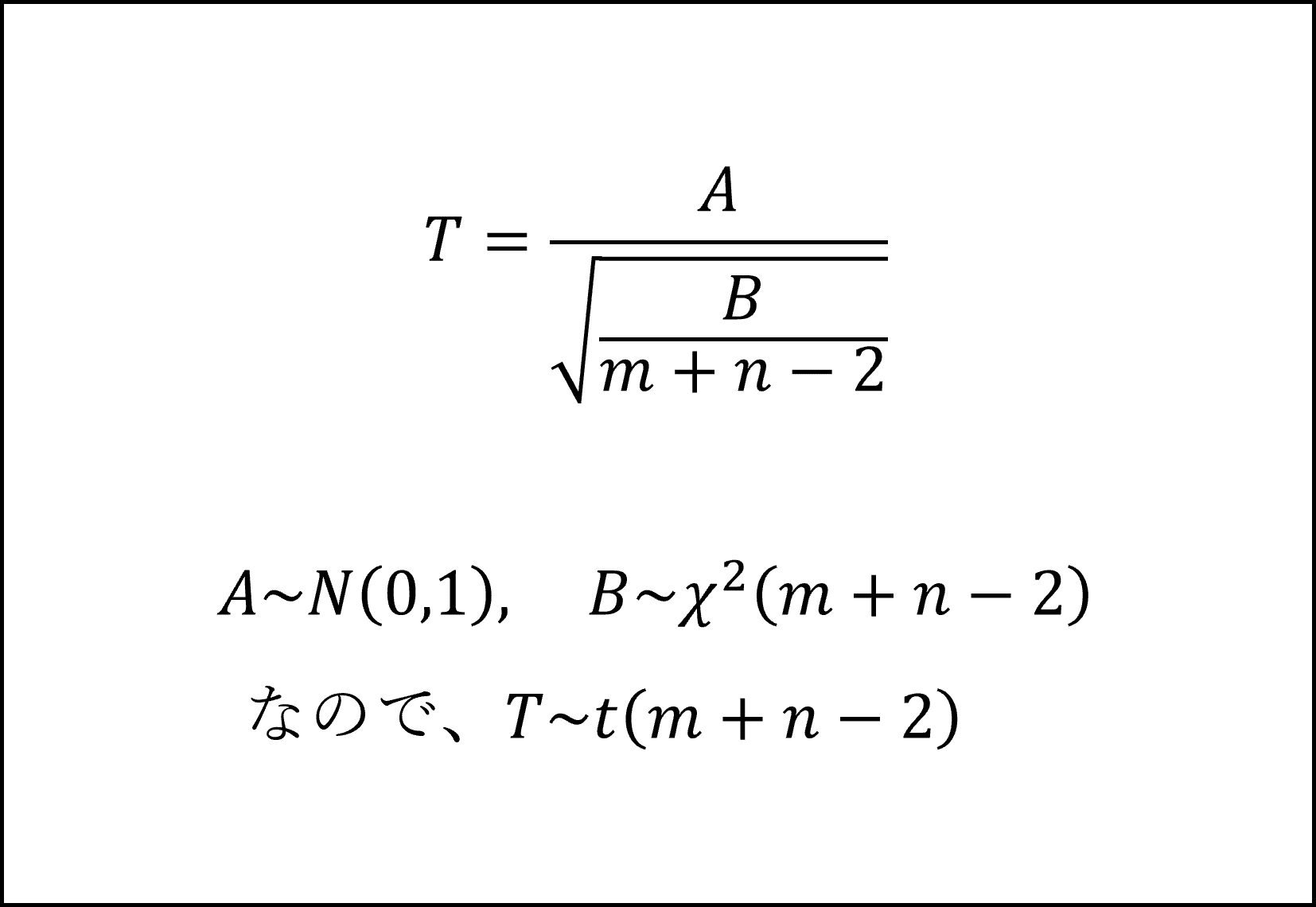
補足

• 標本分布の関係性、つながりを理解しているかが問われる問題です。
• 母平均の差の検定と聞くと、標準正規分布やt分布が想起されますが、その背後にはカイ二乗分布があることを意識させる良問です。
• 標準正規分布、カイ二乗分布、t分布、あるいは、本問では扱われていませんがF分布という4つの標本分布について、しっかりと理解を固めておきましょう。

（26番、以上）

問19 [27番]（2021年6月試験）

テーマ

• 独立性の検定
• 期待度数、観測度数
• カイ二乗分布、標準正規分布
• P-値

正答

選択肢③

解答例

（ア）与えられた観測度数から、期待度数を以下のように整理できます。

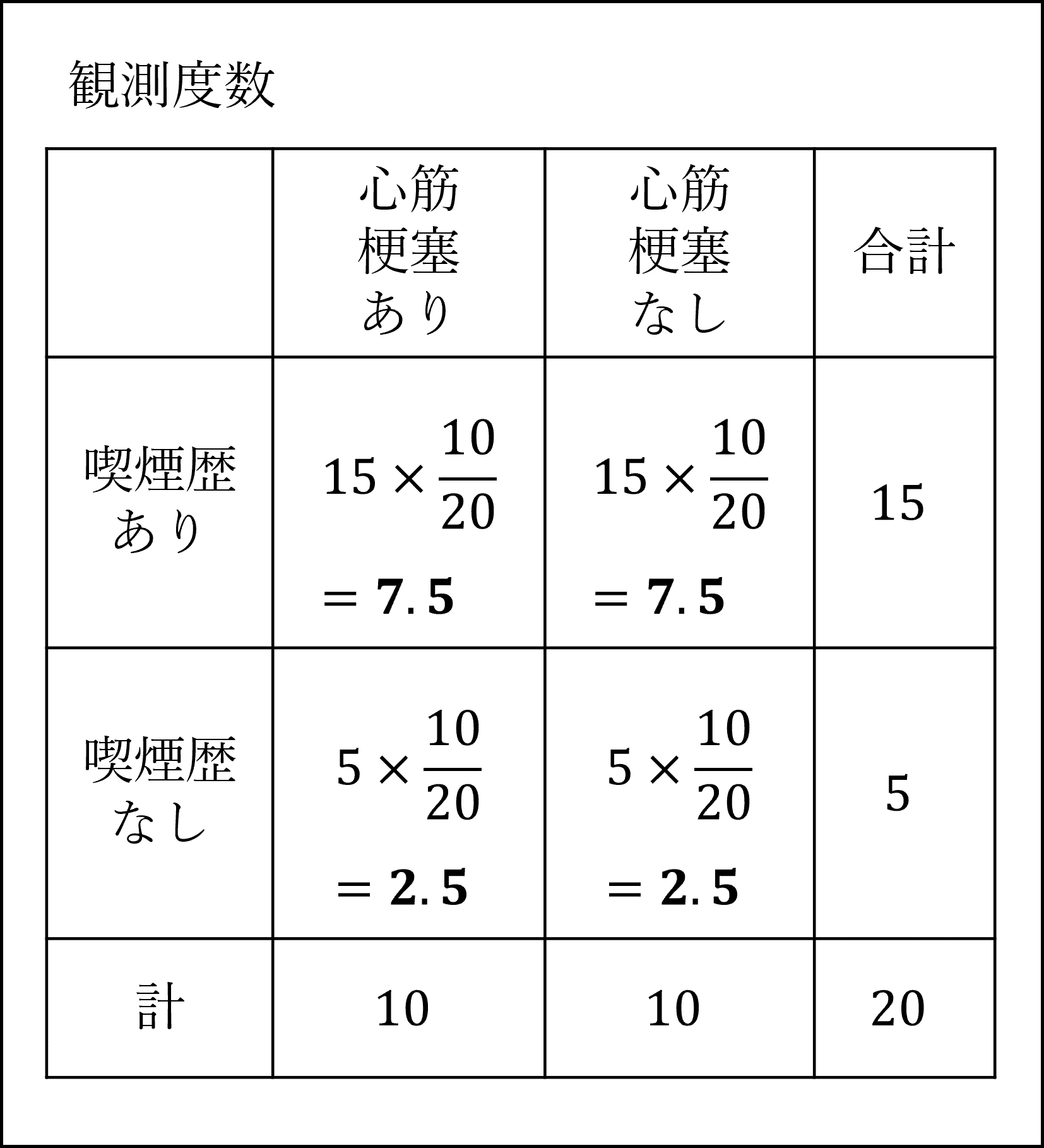
したがって、カイ二乗統計量は

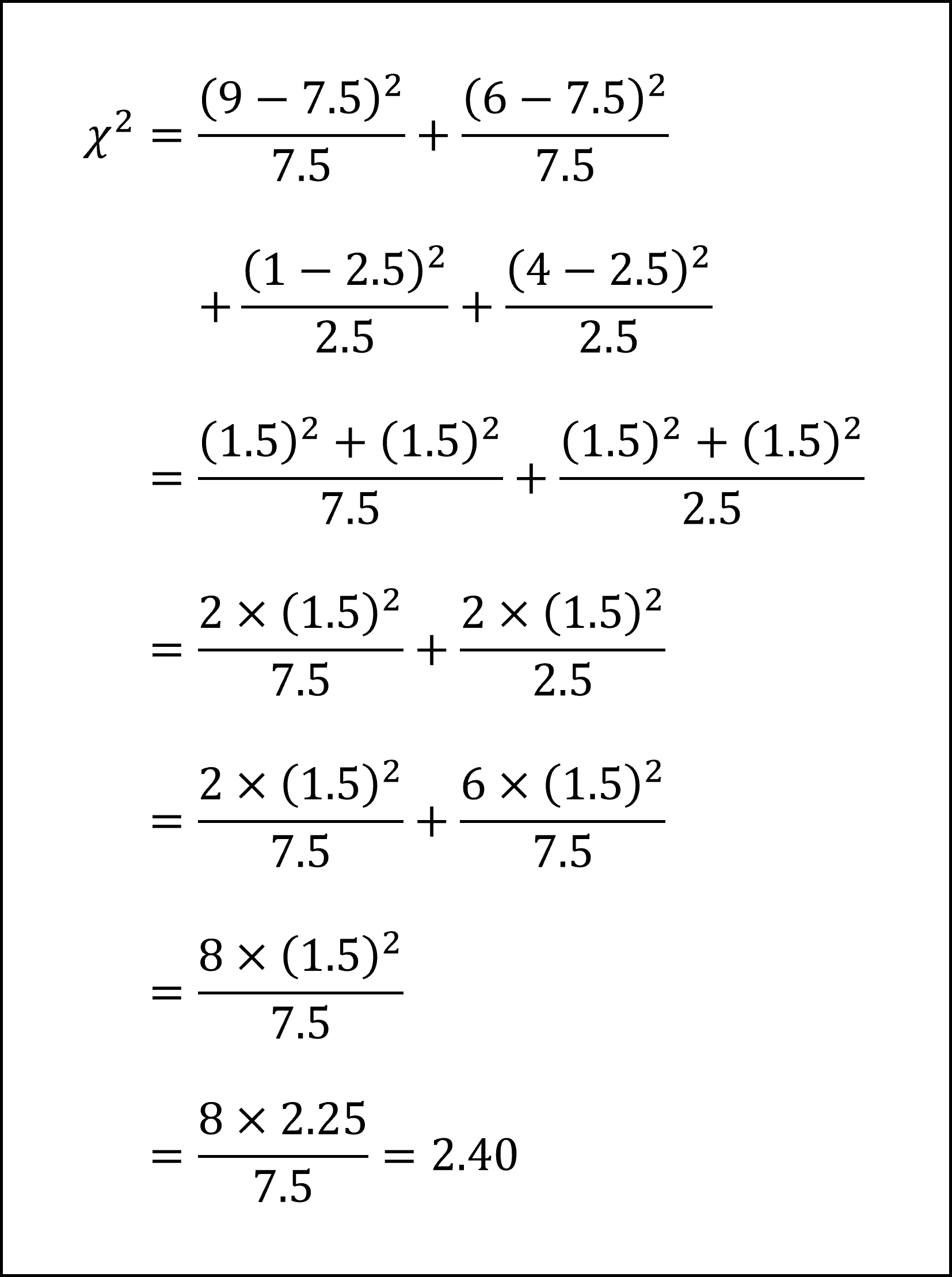
となります。

（イ）上記のカイ二乗統計量がしたがうカイ二乗分布の自由度はクロス集計表の行数と列数を用いて、(行数－1)×(列数－1)＝(2－1)×(2－1)＝1と導かれます。

（ウ）したがって、自由度1のカイ二乗分布におけるカイ二乗統計量の実現値2.40のP-値を調べたいのですが、カイ二乗分布の付表ではP-値が0.10となる点が2.71となるというところまでしか確認できません。

　そこで、自由度1のカイ二乗分布にしたがう確率変数は、標準正規分布にしたがう確率変数の2乗であることを用いて、以下のようにP-値を導きます。

補足

• （ウ）が曲者です。厳密なP-値の値はカイ二乗分布の付表では確認できず、自由度1のカイ二乗分布は標準正規分布にしたがう確率変数の二乗であることを用いて、より詳細に確率を確認できる標準正規分布へと落とし込む必要があります。
• ですが、カイ二乗分布の付表より、自由度1のカイ二乗分布のα＝0.10となる点（上側10%点）、α＝0.05となる点（上側5%点）、α＝0.01となる点（上側1%点）の間隔から、選択肢の消去表で正答を導くこともできそうです。
  例）上側5%点が3.84で、上側10%点が2.70なので、上側15%点はおよそ1.5~2.0くらいだろう…。であればカイ二乗統計量の実現値2.40に対応するP-値は10%（=0.1）と15%（=0.15）の間となるだろうから選択肢③が正答となりそう…。

（27番、以上）

問20 [28番,29番]（2021年6月試験）

テーマ

• 正規分布、標準正規分布
• 第1種の過誤の確率
• 多重検定

正答

[28]選択肢③　[29]選択肢④

解答例

[28番] 第1種の過誤の確率は「帰無仮説が正しいときに、誤って帰無仮説を棄却してしまう確率」です。したがって、問題文中に与えられた以下の「帰無仮説を棄却する条件」が成立する確率を導いていきます。

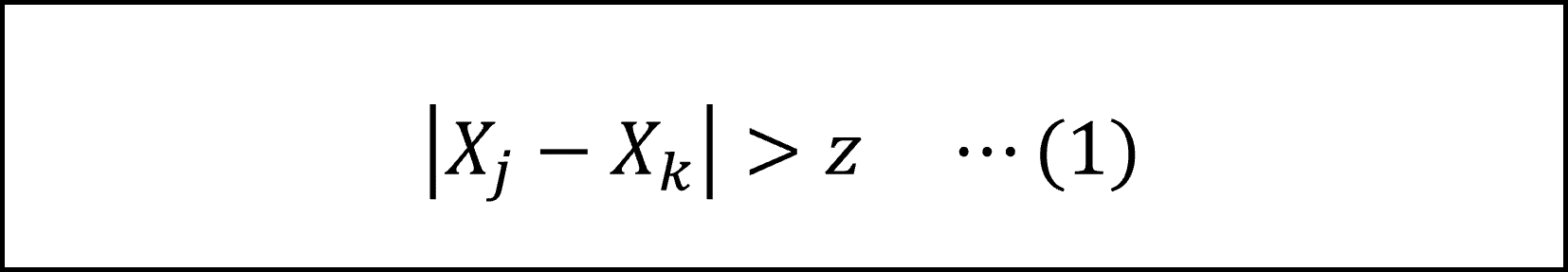
ここで、与えられた条件より

と標準正規分布にしたがう確率変数のかたちに整理できます。

これを念頭に(1)式を整理すると、

となります。以上より、z＝1.96√2のとき、「帰無仮説を棄却する条件…(1)式」が成立する確率（第1種の過誤の確率）は0.05となります。

[29番] (1)式（すなわち、左辺を標準正規分布にしたがうように変形した(3)式）が成立する確率が(5/3)%となればよいので、以下のようにzの値を導くことができます。

補足

• ある確率分布にしたがう確率変数についての、具体的な確率を求める問題は、付表のある標準正規分布などの標本分布にしたがうかたちへと整理することが基本になります。
• [29番]は多重検定（仮説検定を繰り返し実行すること）によって、第1種の過誤の確率（有意水準）を厳しく見積もっておく必要があることを示唆する問題でもあります。

（28番29番、以上）

問21 [30番]（2021年6月試験）

テーマ

• 実験研究におけるバイアス

正答

選択肢③

解答例

選択肢➀：購入時期の順序によるバイアス、対策の順序によるバイアスが生じるため「誤り」です。

選択肢②：購入時期によるバイアス、対策の順序によるバイアスが生じるため「誤り」です。

選択肢③：「正しい」選択肢です。

選択肢④：パソコンによるバイアス、対策の順序によるバイアスが生じるため「誤り」です。

選択肢⑤：パソコンによるバイアス、対策の順序（および作業時間）によるバイアスが生じるため「誤り」です。

補足

• 実験研究においては余計なバイアス、意図しないバイアスを極力排除することが重要です。

（30番、以上）

問21 [31番,32番]（2021年6月試験）

テーマ

• 水準間平方和
• 残差平方和（水準内平方和）
• 自由度
• F分布（F検定）
• t分布（t検定）

正答

[31番]選択肢②　[32番]選択肢⑤

解答例

[31番] 一元配置分散分析において、水準数をa、観測数（サンプルサイズ）をnとすると、水準間平方和の自由度はa-1、残差平方和（水準内平方和）の自由度はn-aになります。
　また、検定統計量Fは分子に水準間平方和の平均、分母に残差平方和の平均をとり、これが自由度(a-1, n-a)のF分布にしたがいます。本問では水準数a=3、観測数n=12ですので、F分布の自由度は(2,9)となります。

[32番] 対策3の効果の点推定値（これは対策3の効果の標本平均になります）をXバー（Xの上側にバーをつけた記号）、対策3の効果の真値をμとおくと、対策3の効果の観測数が4で、誤差項が正規分布N(0,σ^2)にしたがうことを用いて、以下のように整理できます。

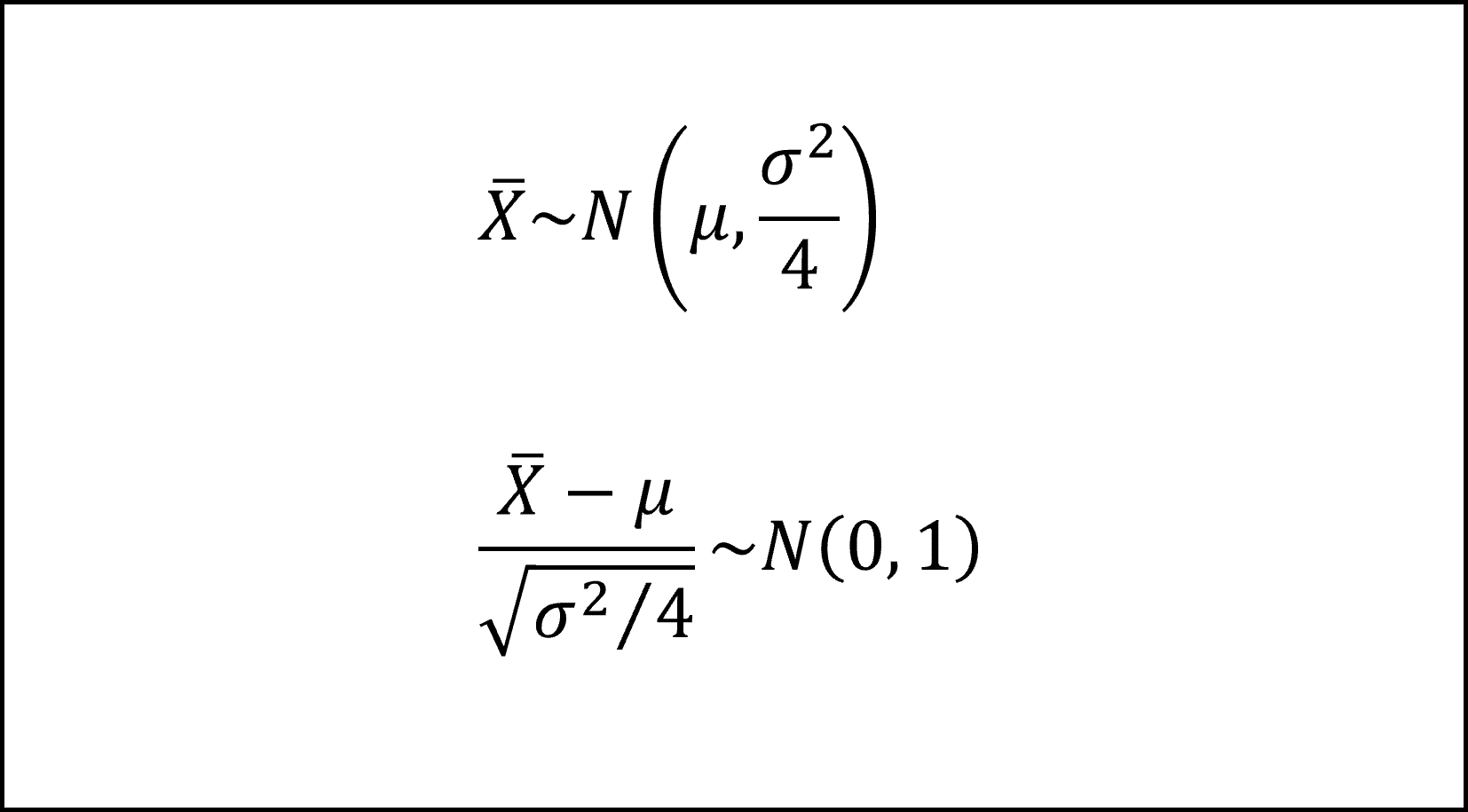
　ここで、誤差項の分散σ^2は未知ですので、これを残差平方和1890.1を自由度n－a＝9で割った値で代用して、以下のようにt分布にしたがうかたちに整理できます。

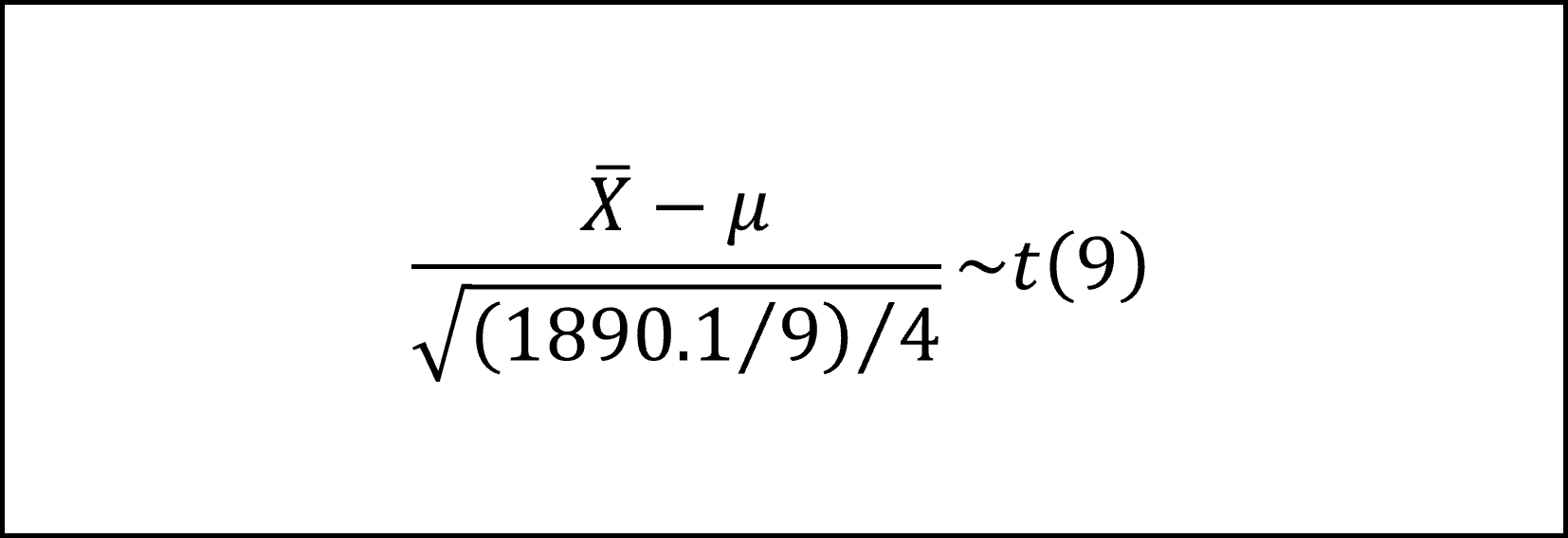
　上記の左辺が自由度9のt分布にしたがいますので、t分布の付表を用いて以下のように対策3の効果の95%信頼区間を導けます。

補足

• [32番]は複雑に見えますが、対策3（の効果）の4つの観測値を用いて、対策3の効果の95%信頼区間を導くというシンプルな区間推定の問題です。
• 対策3の4つの各観測値は誤差項の分布（正規分布）に依存し、その分散も誤差項の分散に等しくなることに注意しましょう。

（31番32番、以上）

問22 [33番,34番,35番]（2021年6月試験）

テーマ

• 偏回帰係数
• t検定、F検定
• 対数モデル
• 決定係数
• 自由度調整済み決定係数

正答

[33番]選択肢⑤　[34番]選択肢②　[35番]選択肢④

解答例

[33番] (ア)には定数項および偏回帰係数の推定量に関して、帰無仮説「推定量の値は0である」のもとで計算される検定統計量tの値が入ります。

　検定統計量tは推定された値（Estimate）を、標準誤差（Std. Error）で割って、以下のように計算できます。

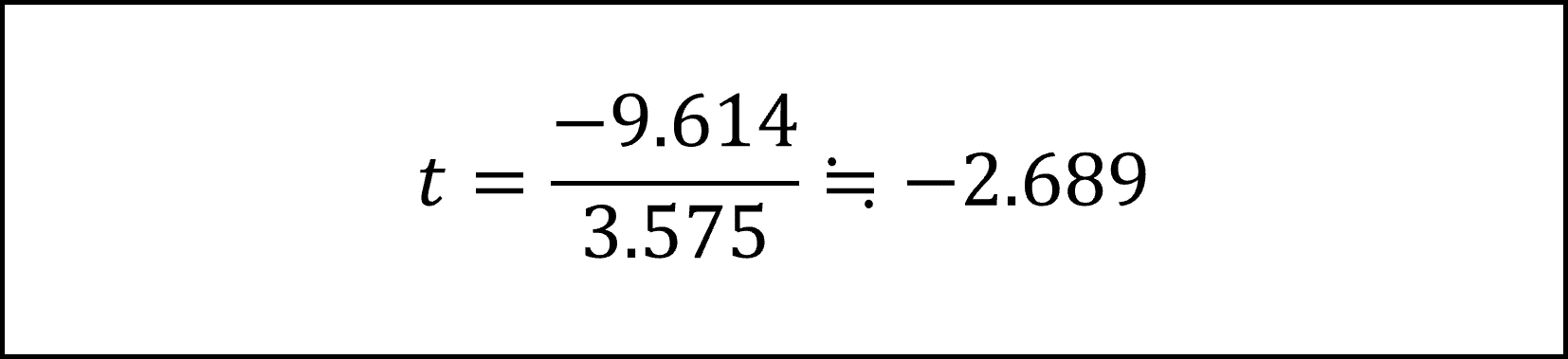
[34番] 【選択肢➀】：説明変数”log(人口密度)”のP-値は9.48e-0.8＝9.48/(10^8)と、定数項のP-値0.010よりも小さいので、定数項のP-値が最も小さいとするこの選択肢は「誤り」です。

【選択肢②】：「正しい」選択肢です。モデルAは以下のように整理できます。

　したがって、「政令指定都市ダミー」以外の変数が同じ値である場合、「政令指定都市をもつ都道府県」であることで「1人当たり社会体育施設数の対数値」が－0.198だけ変動する傾向があると言えます。これを記号を用いて整理すると以下のようになります。

　したがって、政令指定都市をもつ都道府県の「1人当たり社会体育施設数」は、政令指定都市をもたない都道府県のおよそ0.82倍となります（つまり、約2割少なくなる傾向にあります）。

【選択肢③】：15歳未満人口の割合に係る偏回帰係数のP-値は0.333で、有意水準10%で帰無仮説は棄却されませんので「誤り」です。

【選択肢④】：1人当たり所得（の対数）の偏回帰係数は0.519と正の値になっていますので、1人当たり所得が低い都道府県では、1人当たり社会体育施設数が少なくなる傾向にあります。したがって「誤り」です。

【選択肢⑤】：重回帰分析における説明変数の有意性があったとしても、被説明変数への因果関係を裏づけとはなりません。あくまで説明変数と被説明変数の間の相関関係を示唆するもので、因果関係の考察のためには種々の背景事情を考慮した慎重な分析が必要になります。したがって「誤り」です。

[35番] 【選択肢Ⅰ】：「1人当たり所得（の対数値）」はモデルAにおいて有意水準5%で有意でない説明変数ですが、モデルBで除かれていません。したがって「誤り」です。

【選択肢Ⅱ】：モデルAの自由度調整済み決定係数0.8362よりも、モデルBの自由度調整済み決定係数0.8394の方が高いので、「正しい」選択肢です。

【選択肢Ⅲ】：「説明変数にかかるすべての係数が0である」という帰無仮説はF分布を用いたF検定により検定を行います。F検定の結果をみると、モデルA、BともにP-値が極めて小さい値となっていますので、帰無仮説は棄却されます。したがって「正しい」選択肢です。

補足

• 比較的やさしい重回帰モデルの問題ですが、被説明変数や一部の説明変数について対数をとっていることに注意しましょう。
• 特に[34番]の選択肢②については、なぜ正しい選択肢と言えるのか正確に理解しておきたいです。

（番、以上）