カイ二乗分布
正規分布にしたがう標本を X とします。
この X を標準正規分布にしたがうように標準化(平均を引いて標準偏差で割る)した確率変数を z とします。
そして、この z の n 個の二乗の和(平方和)がしたがう標本分布がカイ二乗分布になります。したがって、記号で表記すると以下のように整理できます。
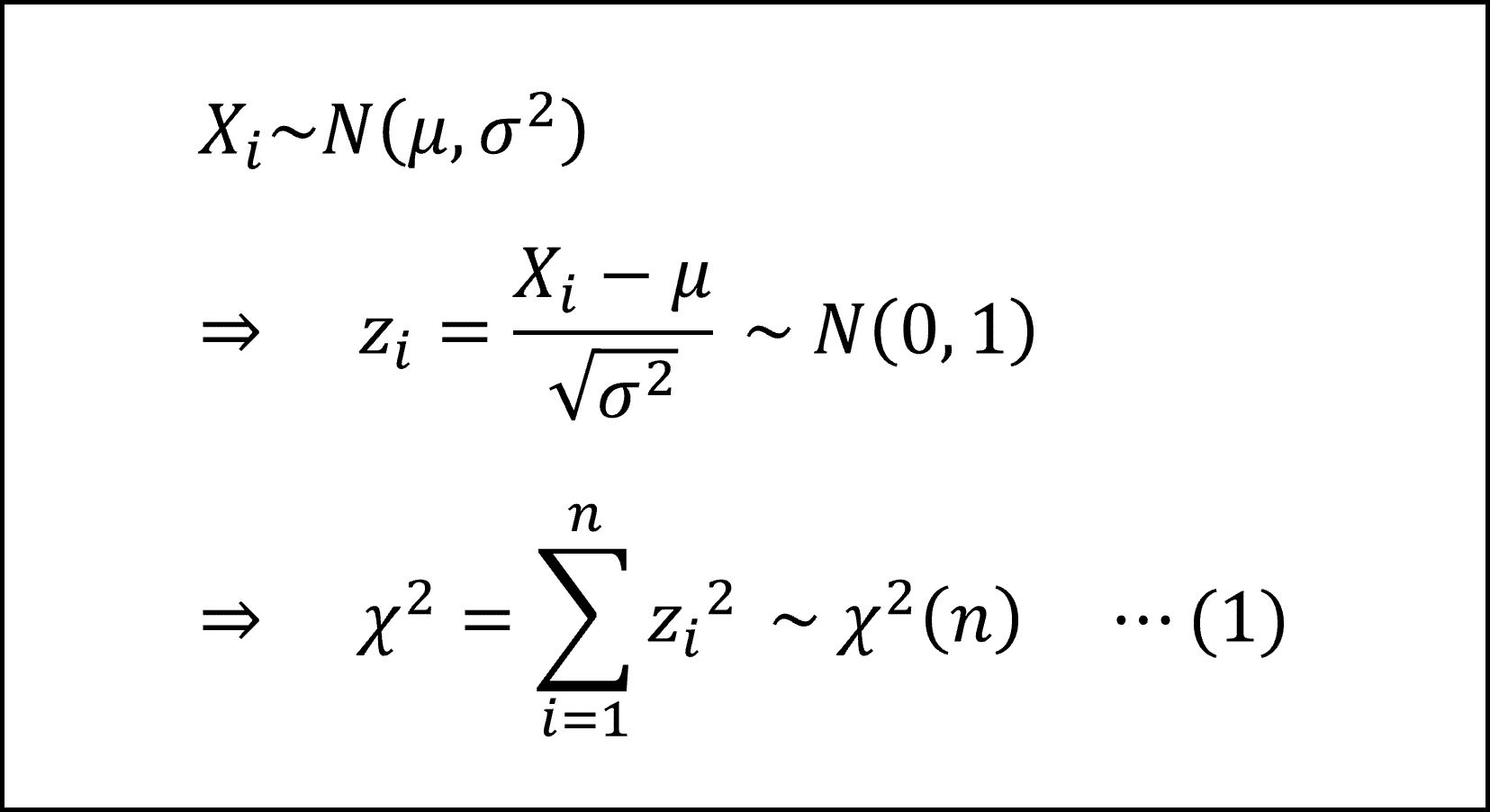
(1)式のカッコ内の n がカイ二乗分布のパラメータである自由度になります。
カイ二乗統計量その1(母分散の区間推定など)
上記の(1)式の z を得るためには母平均 μ が必要になりますが、母平均 μ は基本的には未知です。そこで母平均 μ に標本平均を代用して整理していきます。
まず(1)式の z に標本 X を標準化した分数式を代入して以下のように整理します。
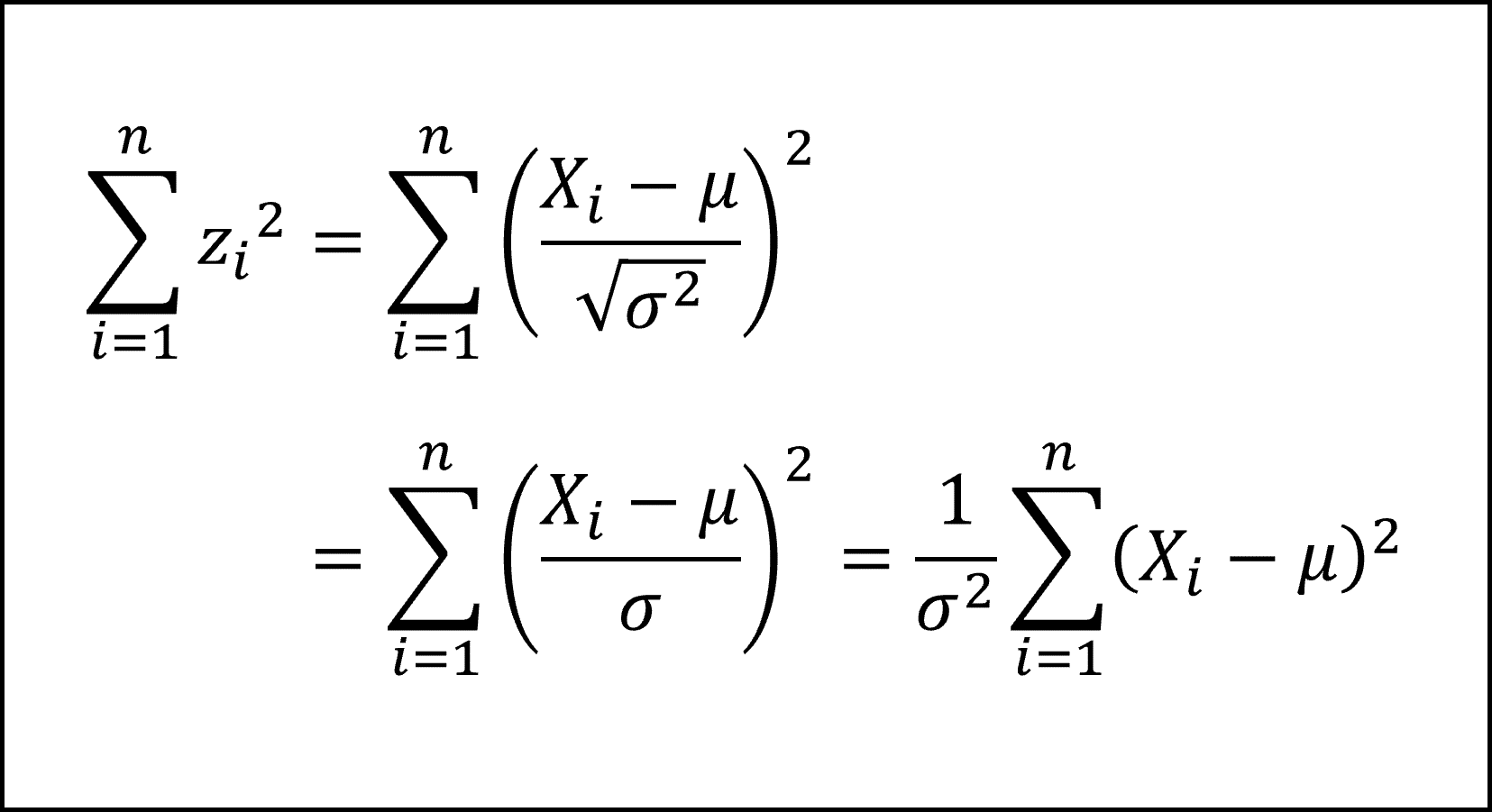
ここで、母平均 μ を標本平均 Xバー でおきかえて、不偏分散をσハット^2とすると、以下のように整理できます。

したがって、(1)式について、不偏分散を用いて以下のように整理しなおすことができます。
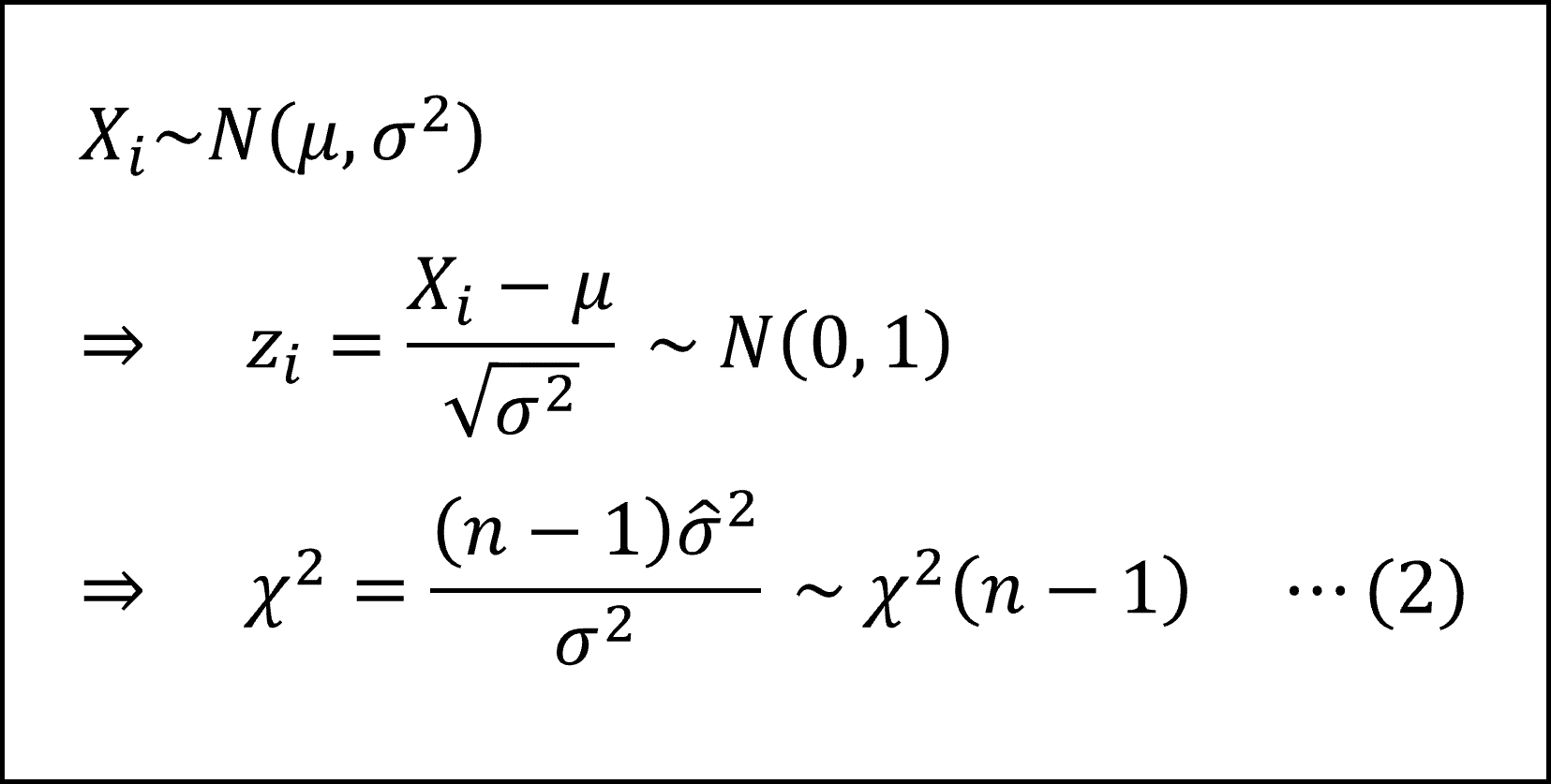
(2)式の分数式がカイ二乗分布にしたがう統計量(カイ二乗統計量)になります。
ポイントは、母平均 μ を標本平均でおきかえたことで、(2)式のカッコ内の自由度は n ではなく n-1 となる点です。
補足
(2)式は母分散の区間推定などに用いられる大切な式で、丸暗記してしまっている方も多いかと思います。
丸暗記でも問題ありませんが、上記のような標準正規分布とカイ二乗分布の関係性を理解しておくことで問題を解きやすくなることもあります(※)。
※例題:2021年06月 問18 [26] ← 標準正規分布・カイ二乗分布・t分布の関係性を問う良問ですのでぜひ取り組んでみてください。
カイ二乗統計量その2(適合度検定)
適合度検定のカイ二乗統計量は以下の式になります。
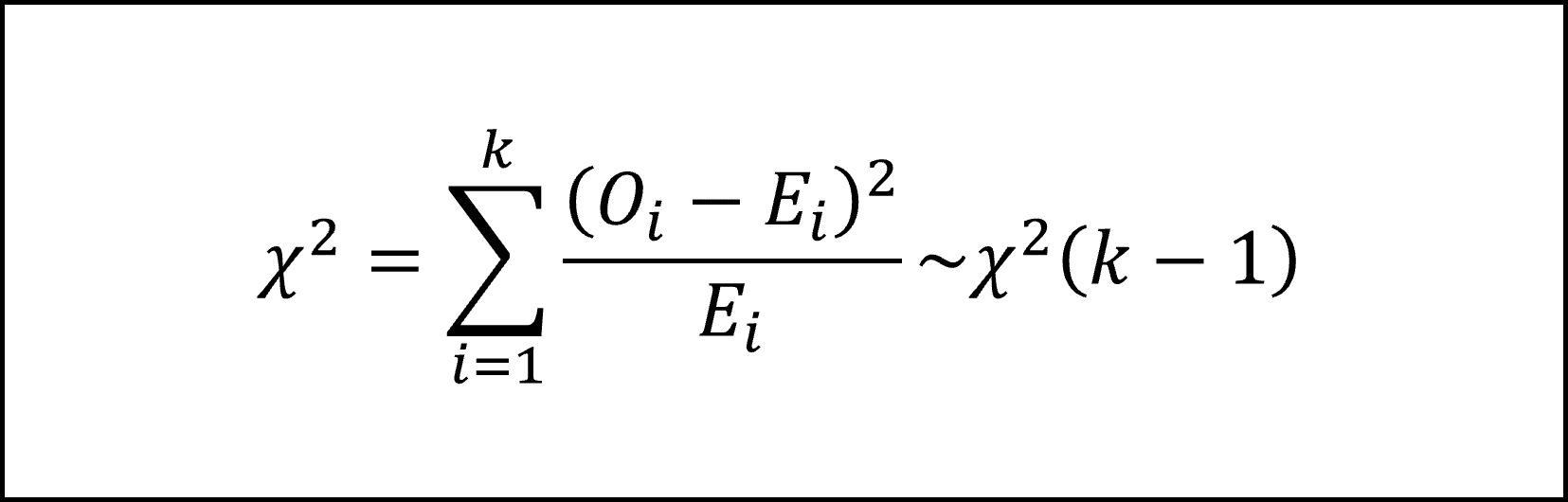
導出(カテゴリ数が2のとき)
以下のような分割表(カテゴリ数 k=2)を考えます。
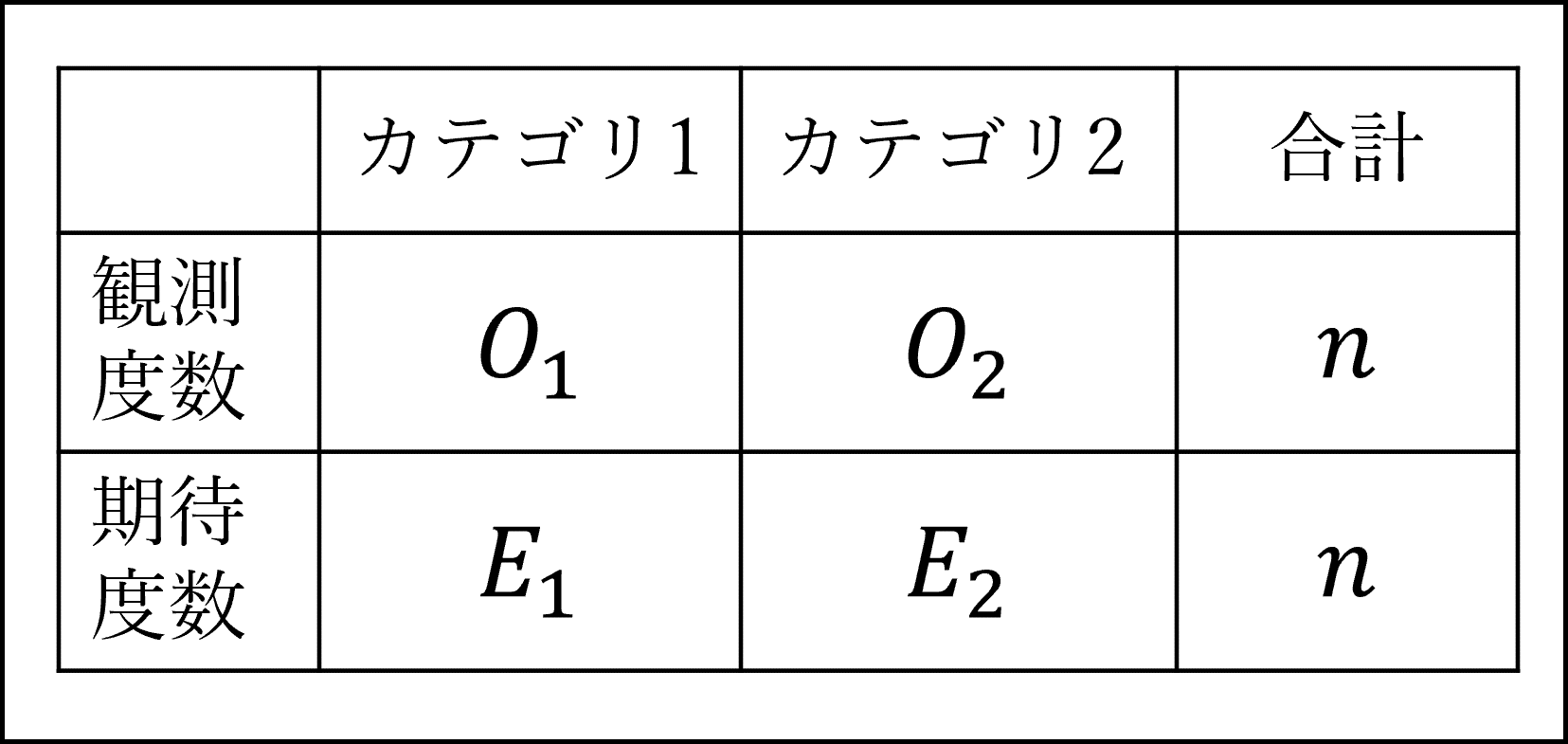
このとき、適合度検定のカイ二乗統計量は以下のような式になります。
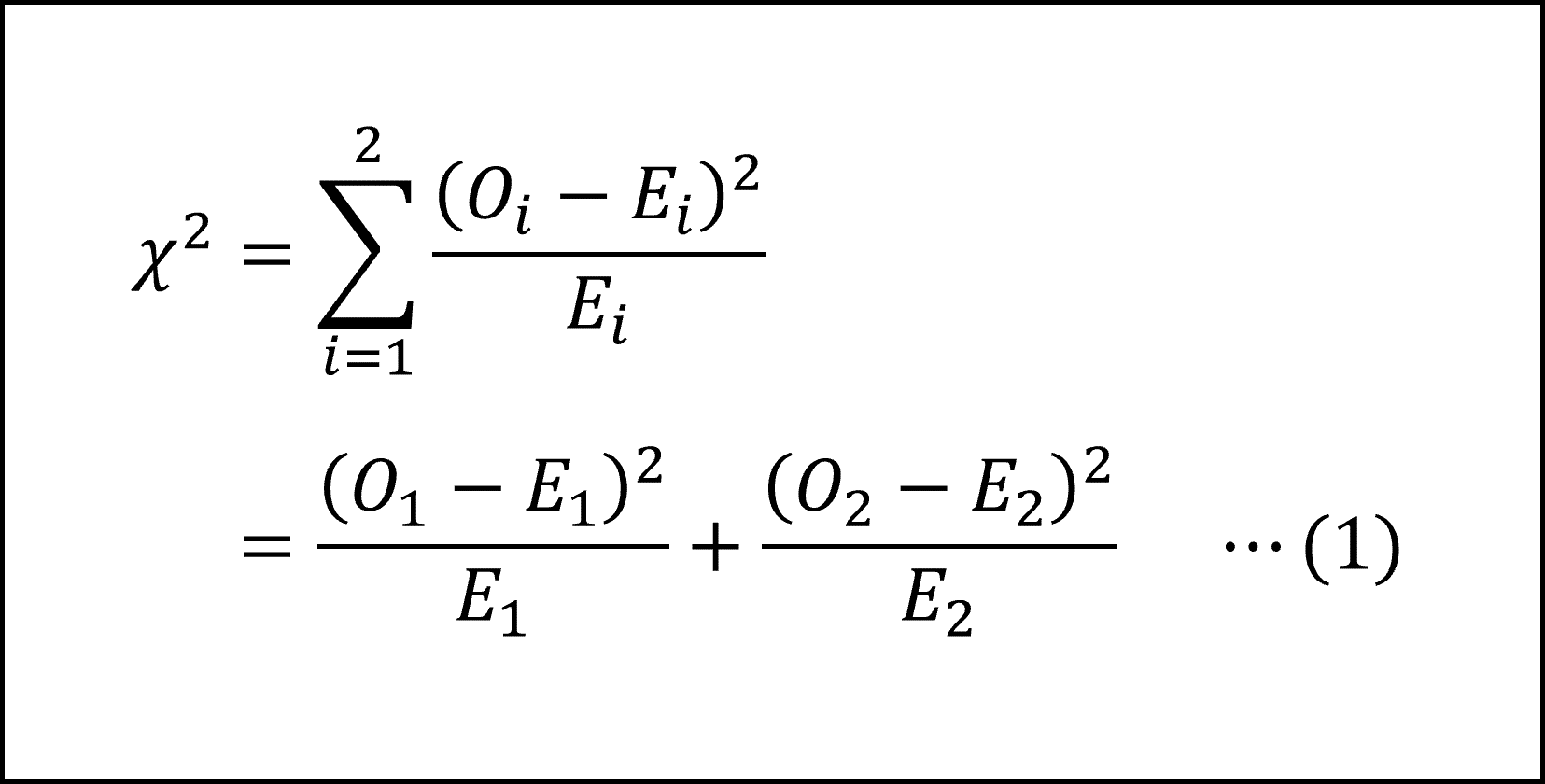
ここで、観測度数の合計、および、期待度数の合計が n であることから
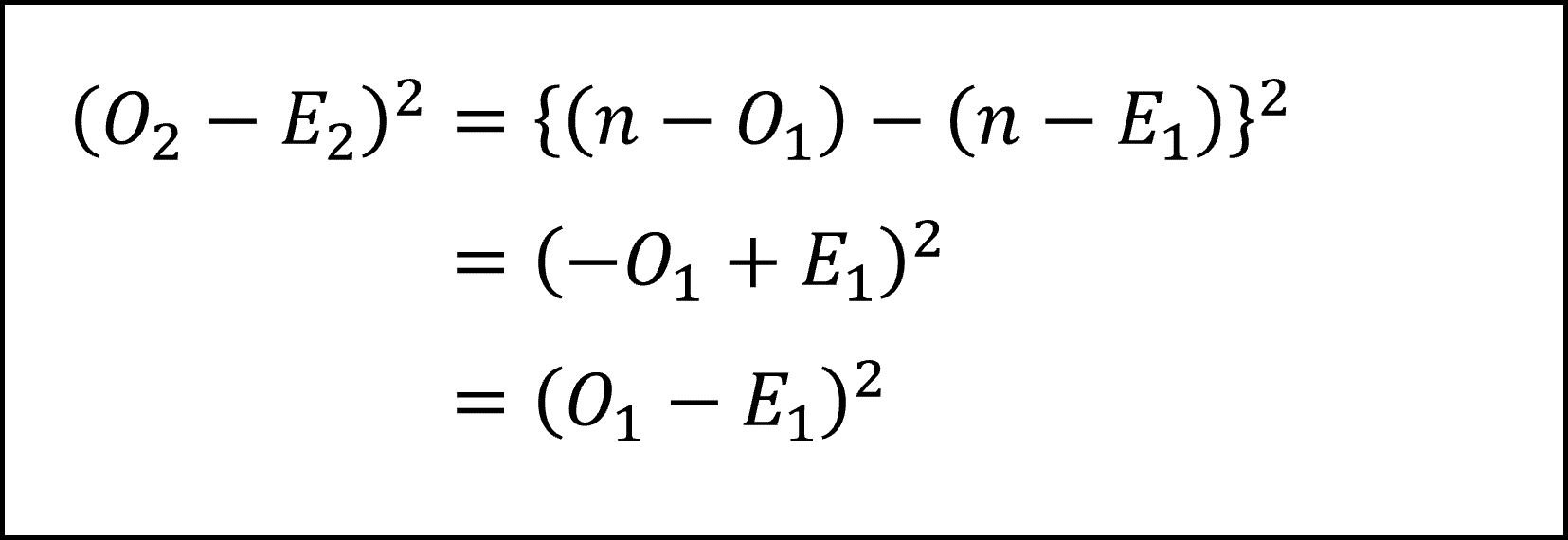
となりますので、これを(1)式に代入して
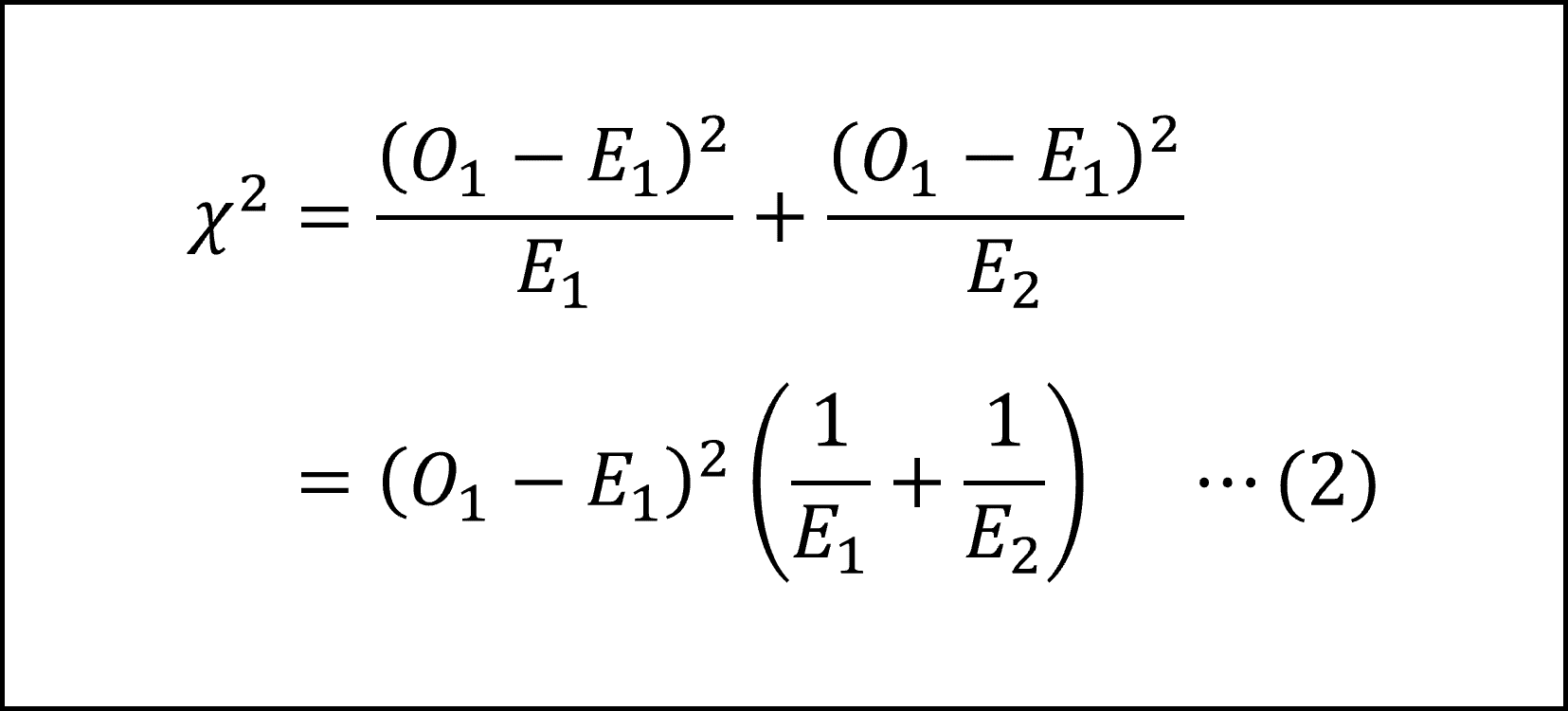
ここで、カテゴリ1となる確率をp1、カテゴリ2となる確率をp2とすると

なので、これを(2)式に代入して
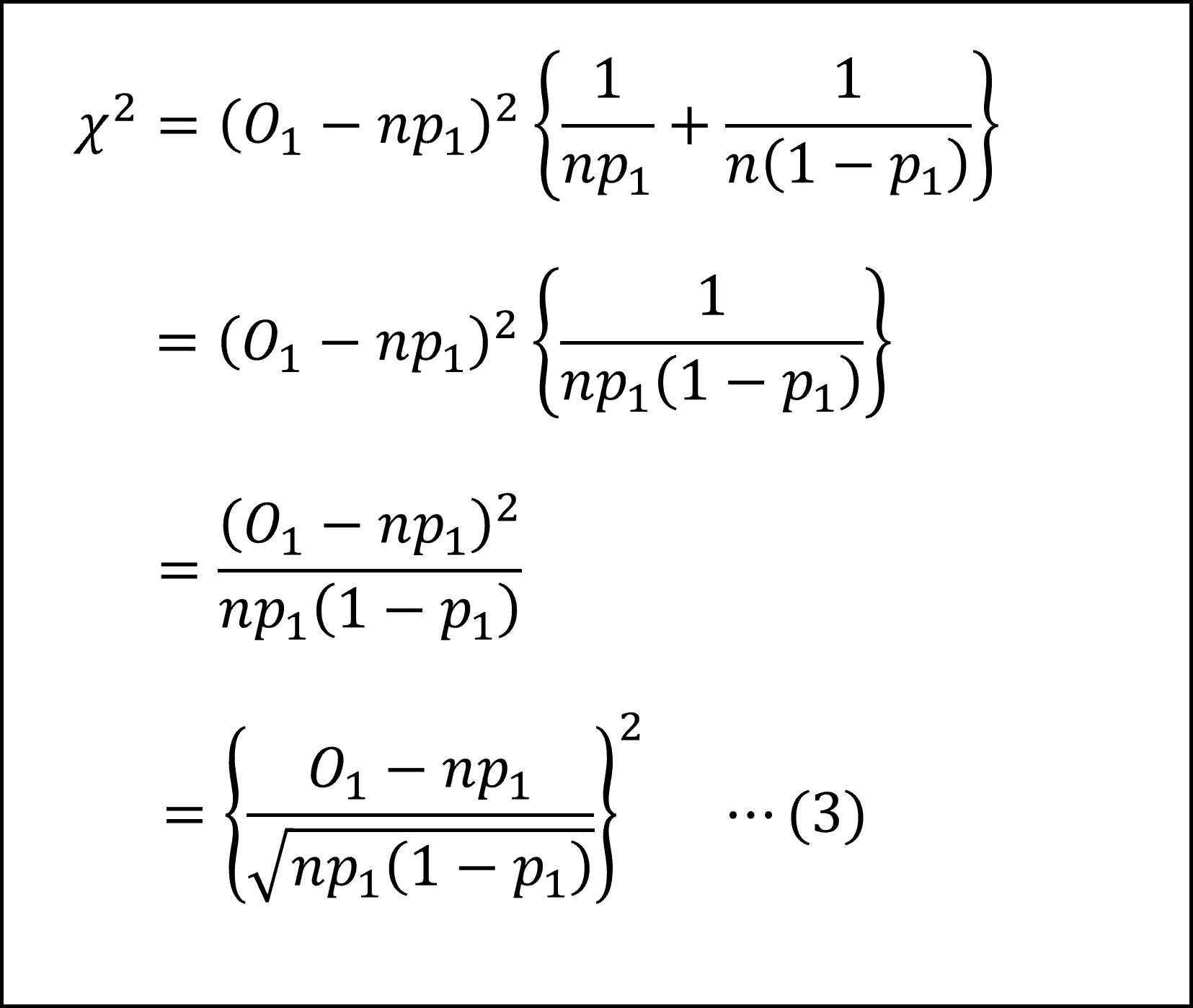
となります。
上記の(3)式がどんな分布にしたがうかを考えます。
まず、カテゴリ1の観測数O1は、試行回数をサンプルサイズ n、成功確率をカテゴリ1となる比率p1とする二項分布にしたがいます。
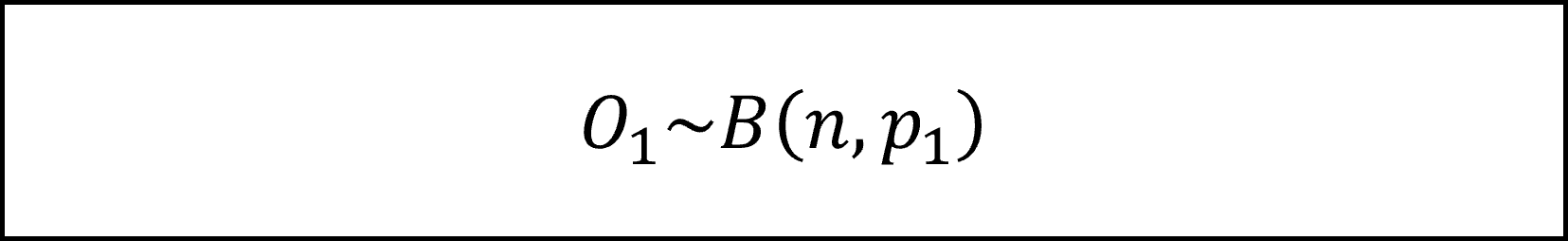
サンプルサイズ n が十分に大きいとき、中心極限定理より二項分布は正規分布に近似しますので
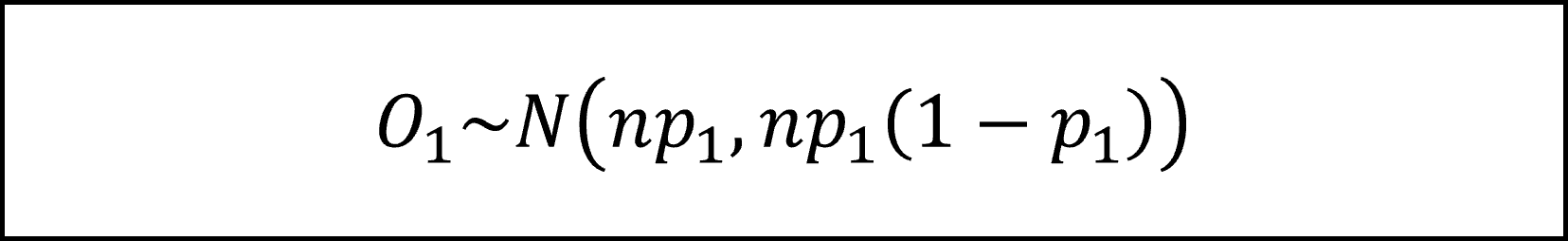
(※二項分布ですので期待値はnp1、分散はnp1 (1-p1 )です)
これを標準正規分布にしたがうかたちに整理(標準化)します。
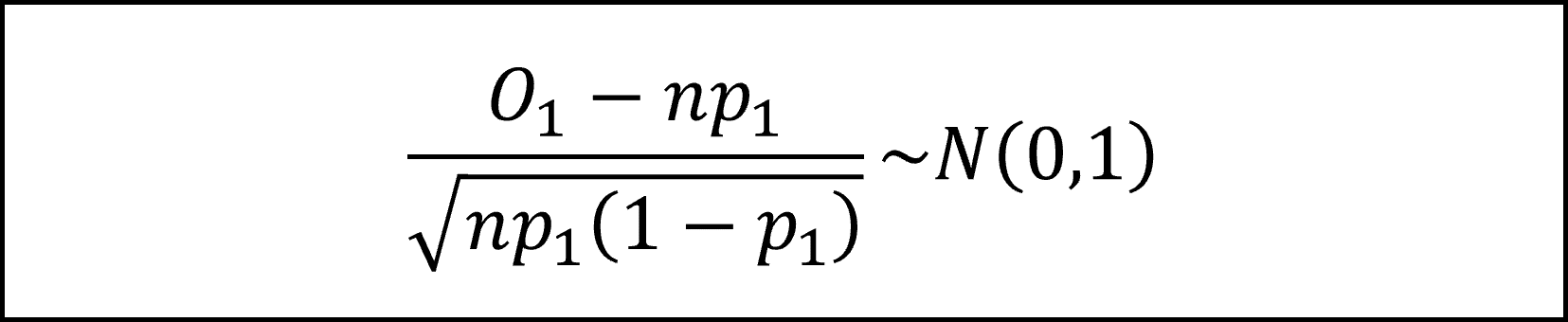
よって、(3)式は標準正規分布にしたがう確率変数の2乗(和)となりますので、以下のように自由度1のカイ二乗分布にしたがうことになります。
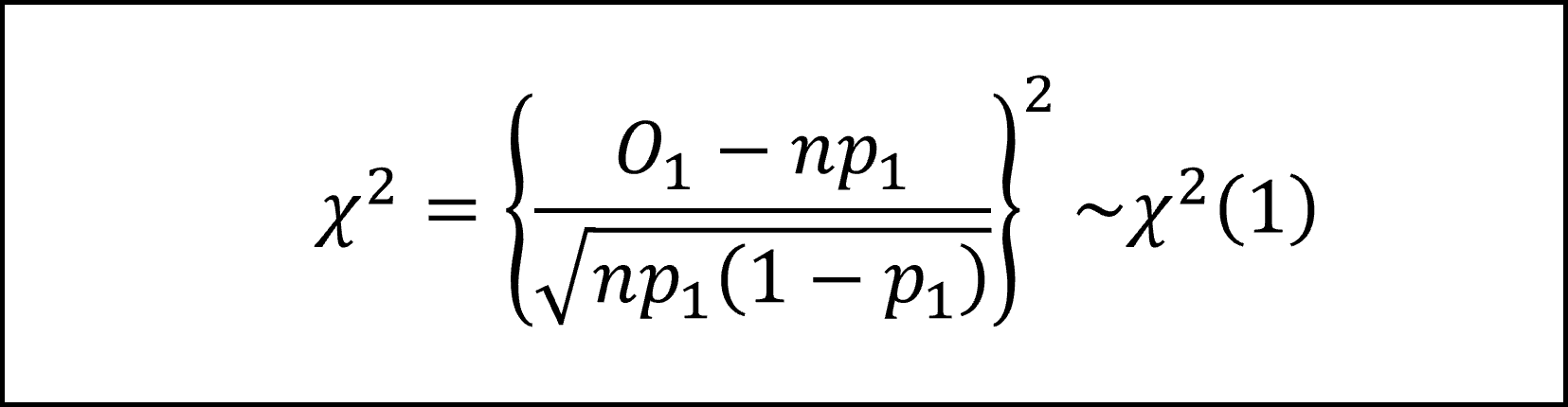
したがって、適合度検定のカイ二乗統計量χ^2が自由度1のカイ二乗分布にしたがうことになります。
(導出以上)
補足
- カテゴリ数が3以上の場合も、上記の考え方を拡張することにより検定統計量がカイ二乗分布にしたがうことを確認できます(詳細は割愛)。
- 二項分布が中心極限定理により正規分布に近似することが前提となっています。そのため、サンプルサイズ n が十分に大きい必要があります。
- カイ二乗分布「標準正規分布にしたがう確率変数Zの二乗の和(平方和)がしたがう分布」であることがポイントです。
(以上)

