
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問01 [01,02番](2019年11月試験)
テーマ
- 箱ひげ図
- 四分位数
- 度数分布表
正答
[1番]選択肢➀ [2番]選択肢③
解答例
[1番]東京の箱ひげ図をみると「16℃以上18℃未満」に2つのプロット(サンプル)が確認できます。度数分布表をみると「16℃以上18℃未満」の度数が2となっているのは(A)のみですので、(A)が東京であることがわかります。
[2番]《選択肢➀》:広島よりも名古屋や大阪、福岡の方が範囲が大きいので「誤り」です。
範囲(=最大値-最小値)と四分位範囲(=第3四分位数-第1四分位数)を混同しないように気をつけましょう。
《選択肢②》:四分位範囲は名古屋よりも東京の方が小さいので「誤り」です。
《選択肢③》:「正しい」選択肢です。
《選択肢④》:中央値(=箱の中の線)は大阪よりも福岡の方が大きいので「誤り」です。
《選択肢⑤》:最大値は東京よりも福岡や大阪の方が大きいので「誤り」です。
補足
- 箱ひげ図は一つの図で複数のカテゴリ別の分布を概観するのに便利な図です。
- 本問の注釈にある「ひげの引き方」や「外れ値の定義」は一般的なものになりますので、この機会に覚えておきましょう。
(01,02番、以上)
問02 [03番](2019年11月試験)
テーマ
- 散布図
正答
選択肢④
解答例
《選択肢➀》:1990年において女性の50歳時未婚率が8%を超えている都道府県は1つしかないので「誤り」です。
《選択肢②》:1990年において男性の50歳時未婚率が10%以上である都道府県が2つありますので「誤り」です。
《選択肢③》:男性の50歳時未婚率は、1990年における最大値が10~11%程度で、2015年における最小値が18%程度ですので、2015年よりも1990年の方が低い都道府県はありません。よって「誤り」です。
《選択肢④》:「正しい」選択肢です。2015年の散布図から明らかです。また、女性の50歳時未婚率(y)=男性の50歳時未婚率(x)となる直線を引いたとき、すべてのプロットが直線よりも下側(y<x)にあることからも確認できます。
《選択肢⑤》:女性の50歳時未婚率が最も低い都道府県の男性の50歳時未婚率は19%程度ですが、男性の50歳時未婚率が18%程度の都道府県が2つありますので「誤り」です。
補足
- 散布図は横軸と縦軸を見失わないことが大切です。
(03番、以上)
問02 [04,05番](2019年11月試験)
テーマ
- 散布図
- 相関係数
- ヒストグラム
正答
[4番]選択肢④ [5番]選択肢③
解答例
[4番]散布図のプロットが直線上にあるほど相関係数(の絶対値)は大きくなります。1990年の散布図の方が2015年の散布図よりも「直線上」にデータが分布していますので、「1990年の相関係数 > 2015年の相関係数」であることがわかります。
「1990年の相関係数 > 2015年の相関係数」となっている選択肢は①と④ですが、①は散布図と見比べて相関係数が小さすぎますので、④が正答となります。
[5番]散布図から18%以上である都道府県は1つ、16~18%である都道府県は5つです。18%以上の階級の度数が1で、16~18%の階級の度数が5となっているヒストグラムは選択肢③になります。
補足
- この機会に本問の1990年の散布図が相関係数0.7くらい、2015年の散布図が相関係数0.4くらいと脳裏に焼き付けておきましょう。
- 散布図は鳥の目(俯瞰)と虫の目(詳細)の双方の目で見ることを意識しましょう。
(04,05番、以上)
問03 [06,07番](2019年11月試験)
テーマ
- 指数化
- 指数の実数変換
- 平均変化率
- 幾何平均
正答
[6番]選択肢① [7番]選択肢④
解答例
[6番]平成31年1月の賃金指数をXとすると、Xの平成30年12月からの変化率は以下の式になります。
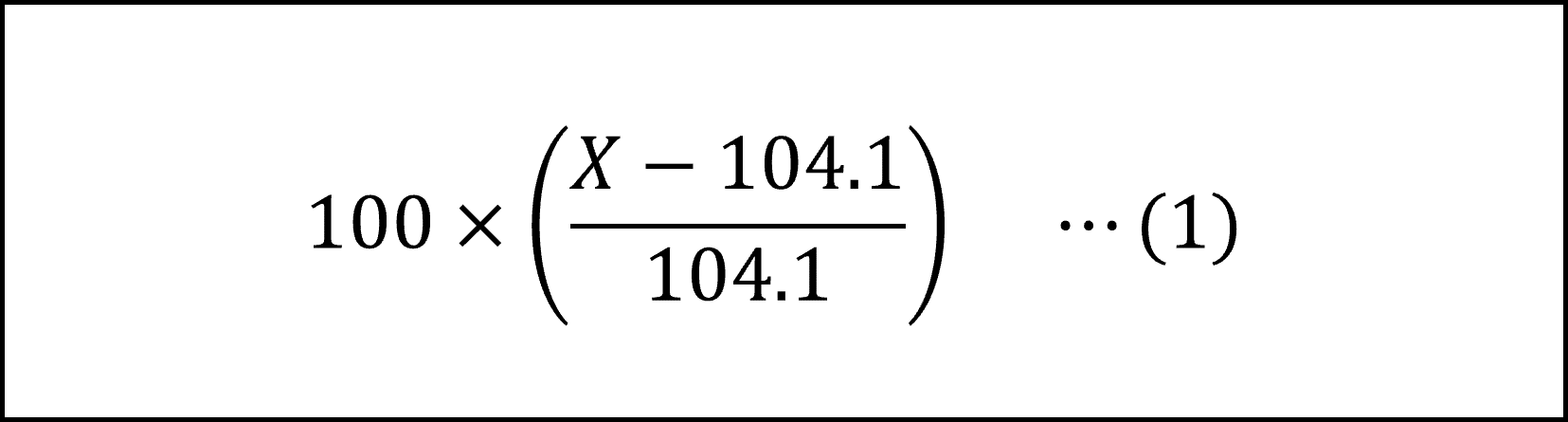
ここで、問題文より Xは平成30年1月の賃金指数102.6からの変化率が-0.97%(=-0.0097)ですので、X=102.6+102.6×(-0.0097)=102.6×(1-0.0097)となります。これを(1)式に代入して整理すると以下のようになります。
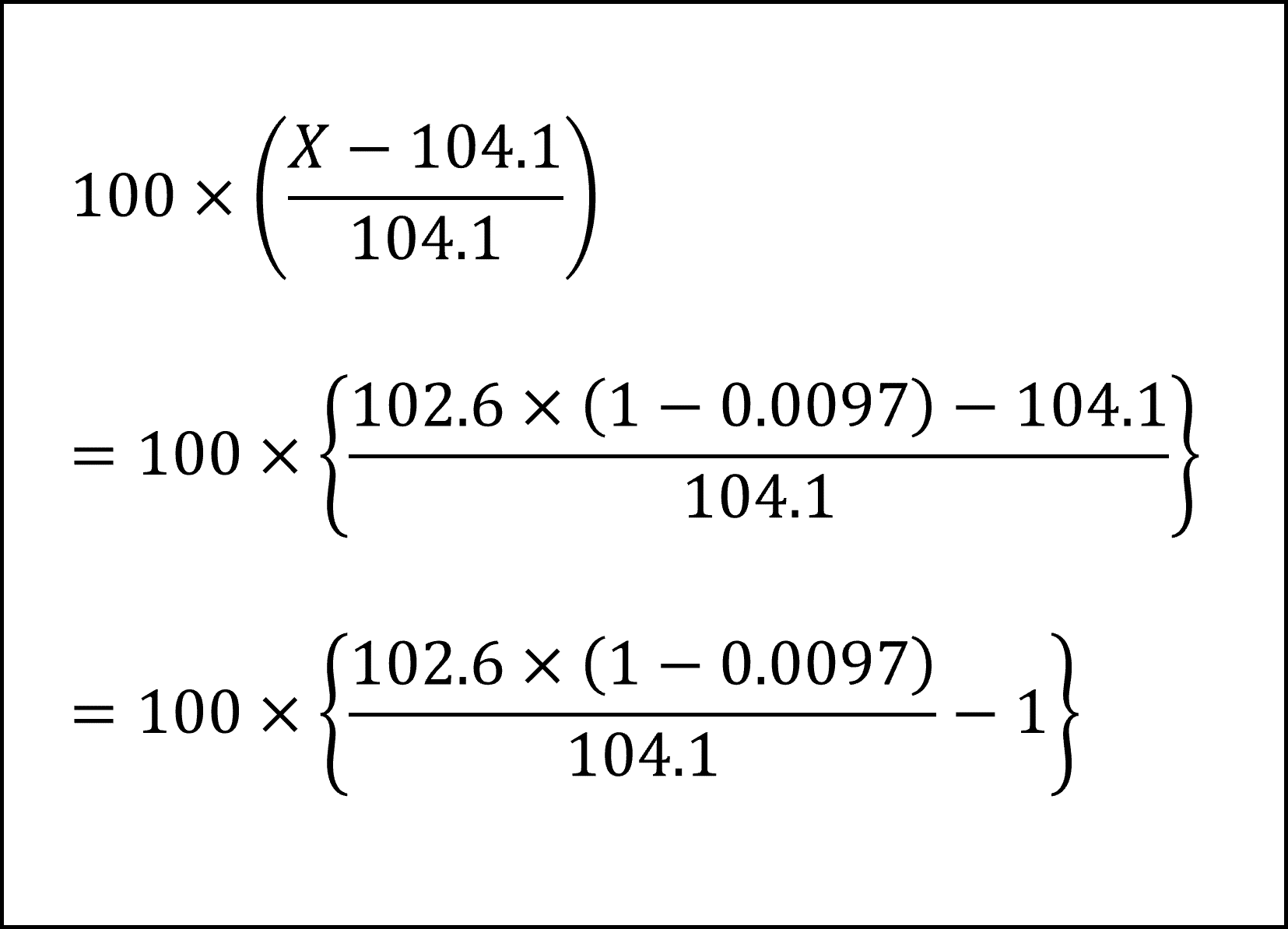
[7番]平成30年1月から同年4月までの3ヶ月における1カ月あたりの平均変化率 r %(= r /100) を、単純平均ではなく「幾何平均」により計算する問題です。期間が3ヶ月ですので、以下のように計算します。

補足
- 幾何平均のポイントは「期間」です。基準時点から比較時点までの期間に注目しましょう。
- 本問では平均変化率 r の単位が%となっていることにも注意しましょう。
(06,07番、以上)
問04 [08番](2019年11月試験)
テーマ
- 時系列データの変動
- 傾向変動
- 季節変動
- 不規則変動
正答
選択肢②
解答例
時系列データは時間の経過によって変動するデータです。その変動は「傾向変動」「季節変動」「不規則変動」に分けられます。
[記述Ⅰ]:傾向変動は常に直線的なものとは限らないので「誤り」です。
[記述Ⅱ]:季節変動は周期1年で循環する変動ですので「正しい」内容です。「1年」を周期とするという点がポイントです。
[記述Ⅲ]:不規則変動には予測困難な偶然変動が含まれますので「誤り」です。
補足
- 時系列データの変動分解は見落としがちですが試験範囲に含まれていますので忘れずに理解しておきましょう。
(08番、以上)
問05 [09番](2019年11月試験)
テーマ
- コレログラム
- 時系列データ
- 自己相関係数(ACF)
正答
選択肢②
解答例
コレログラムは横軸にラグ(Lag)、縦軸に自己相関係数(ACF)をとったグラフです。ラグというのは元のデータからずらした期間を表します。
例えばコレログラムの横軸が12のときに縦軸が0.7であれば、元のデータと12ヶ月後のデータとの(自己)相関係数が0.7である…と読み取れます。
元の折れ線グラフの時系列データを見ると、ガス販売量が12ヶ月周期で似たような推移をしており、ラグ12、24、36前後の自己相関係数が高くなっている(正の相関がある)と推察されます。
また、ガス販売量は12~2月頃に増加、6~8月頃に減少するような、6か月ごとに逆の動きとなるような推移となっています。そのため、ラグ6前後の自己相関係数は低くなっている(負の相関がある)と推察されます。
以上より選択肢②のコレログラムが正答となります。
補足
- コレログラムだけでなくグラフは必ず横軸と縦軸を正しく理解することからスタートしましょう。
(09番、以上)
問06 [10番](2019年11月試験)
テーマ
- 単純無作為抽出法
- 層化抽出法
- 集落(クラスター)抽出法
正答
選択肢④
解答例
[記述Ⅰ]:母集団から単純無作為に(どの個体も等しい確率で)抽出されるので「単純無作為抽出法」になります。
[記述Ⅱ]:午前と午後のグループ(層)別に抽出するため「層化抽出法」になります。
[記述Ⅲ]:全体の搭乗客を「便(集落)」で分けて、そのなかの一部の便(集落)の搭乗客を全数調査していますので「集落抽出法」になります。
補足
- なお記述Ⅱの層化抽出法は、層(グループ)に分けることで層内の分散が小さくなり、推定精度が向上します。
- 集落抽出法はクラスター抽出法とも呼ばれ、一部の群を「全数」調査するという点がポイントになります。
(10番、以上)
問07 [11番](2019年11月試験)
テーマ
- 標本平均の分散
- 標準誤差
正答
選択肢③
解答例
標本平均の性質より、標本平均の分散は、母集団の分散σ^2を標本の大きさ n で割った以下の式になります。
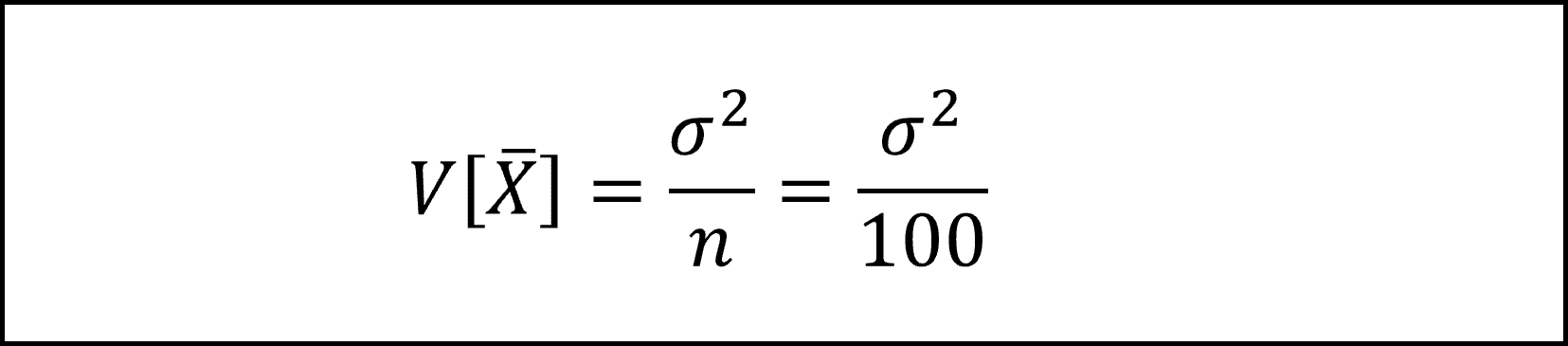
ここで、標本平均の標準誤差(=標本平均の標準偏差を推定した値)は、母集団の分散σ^2に不偏分散を代用し、以下のように導けます。
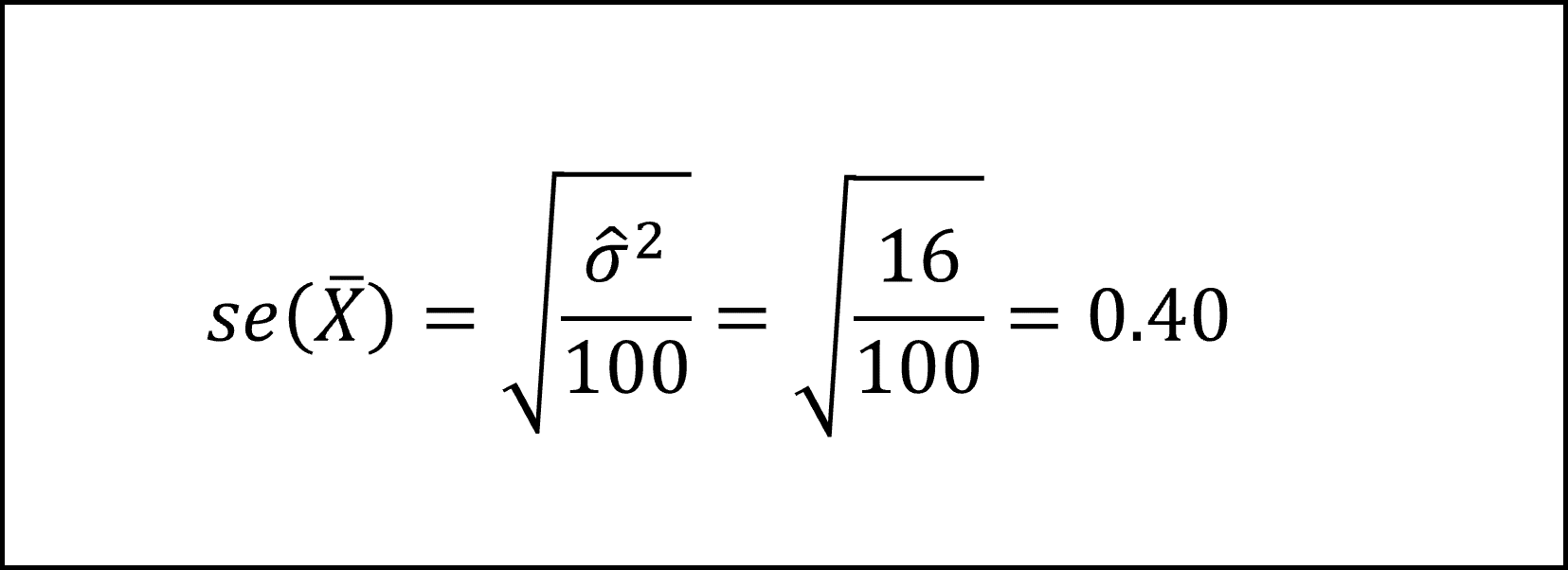
補足
- 標本平均の標準誤差は「標本平均の標準偏差を推定した値」になります。
- 母分散が未知ですので、標本平均の標準偏差も未知ですが、不偏分散で母分散を推定してあげることで標本平均の標準偏差を推定することができます。そうして標準偏差を推定した値が、まさに「標準誤差」となります。
(11番、以上)
問08 [12,13番](2019年11月試験)
テーマ
- 条件付き確率
正答
[12番]選択肢① [13番]選択肢③
解答例
はじめに問題文の条件から、全体を1(=100%)として確率分布の表を作成しておきます。
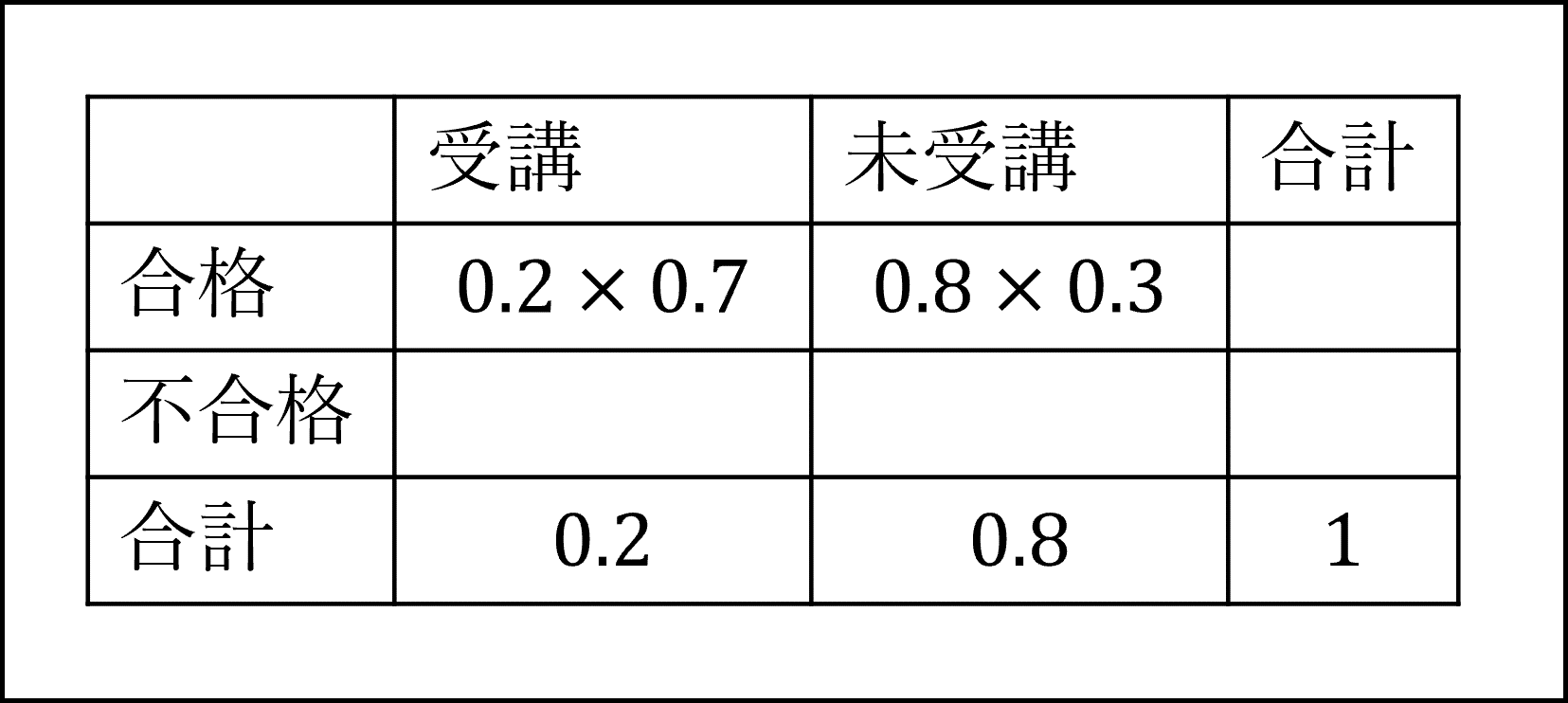
[12番]対策講座を受講していて、かつ、合格者である確率は、上記の確率分布の表の左上のセルの確率になります。よって、0.2×0.7=0.14になります。
[13番]全体をn=1000人として上記の確率分布の表に基づいて分布表を埋めると以下のようになります。
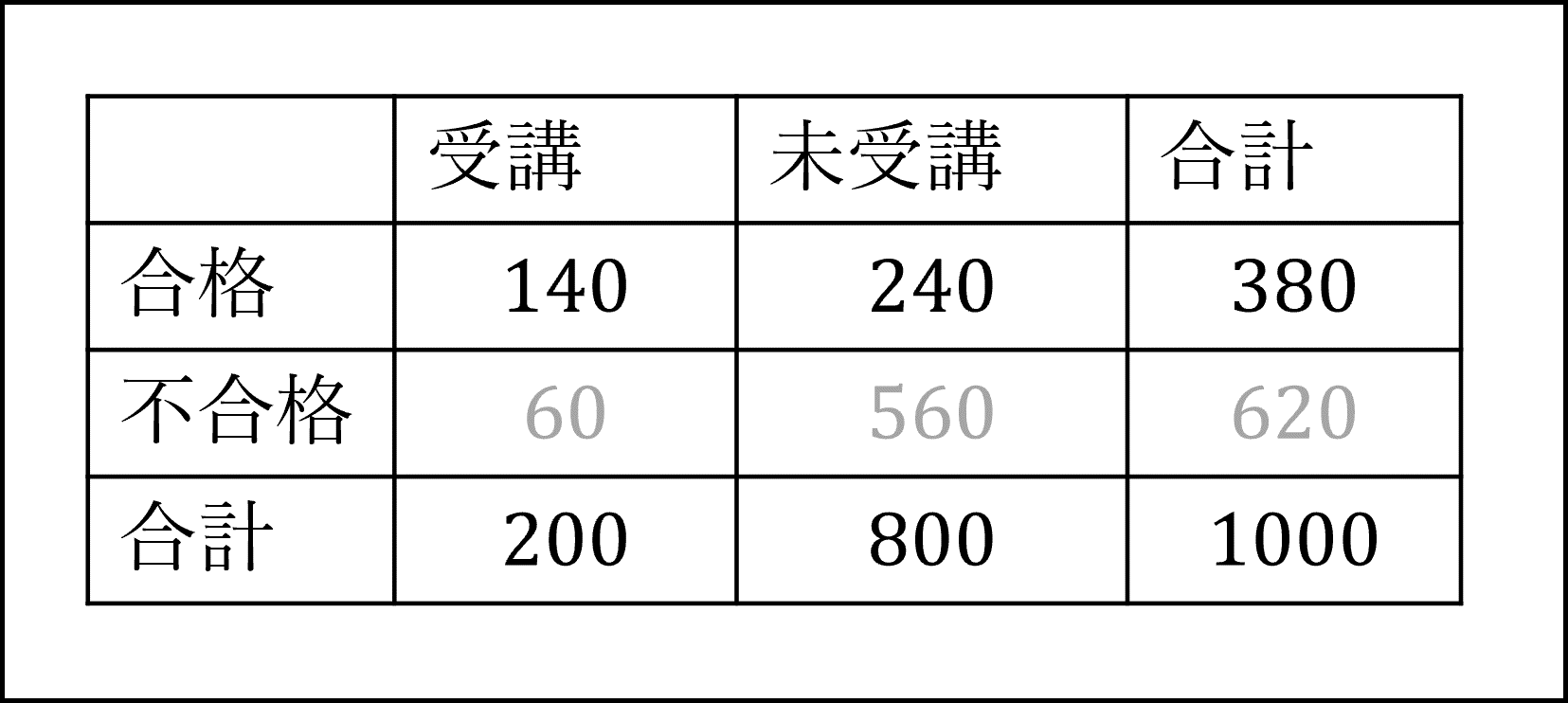
合格者のうちの、対策講座の受講生の確率を計算すればよいので、
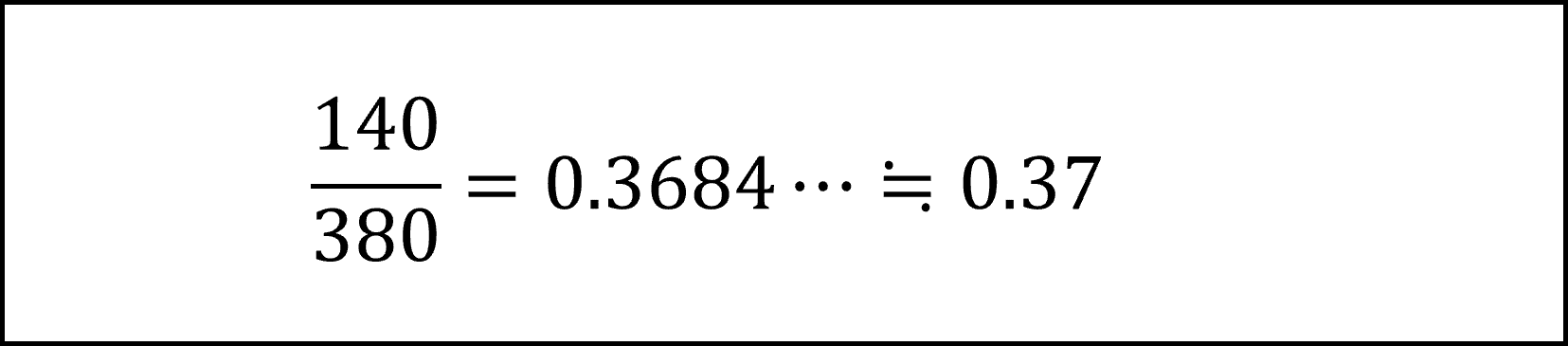
が正答となります。
補足
- 条件付き確率の問題は上記のような確率分布表を書くことをおすすめしております。
- 上記の140/380は、以下の式と同義で、これはまさにベイズの定理の公式になります。
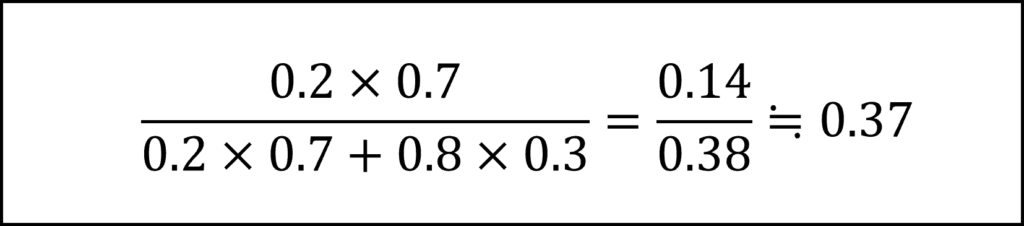
- n=1000など比較的大きな実数を仮定して実数で計算した方が混乱しにくいため、本サイトではベイズの定理の公式に頼らない上記の方法での条件付き確率の計算方法をご紹介しております(ただ、やっていることはベイズの公式と同じです)。
(12,13番、以上)
問09 [14,15,16番](2019年11月試験)
テーマ
- 確率密度関数
- (定)積分
- 確率変数の期待値
正答
[14番]選択肢④ [15番]選択肢④ [16番]選択肢②
解答例
[14番]与えられた確率密度関数を図にすると以下のようになります。
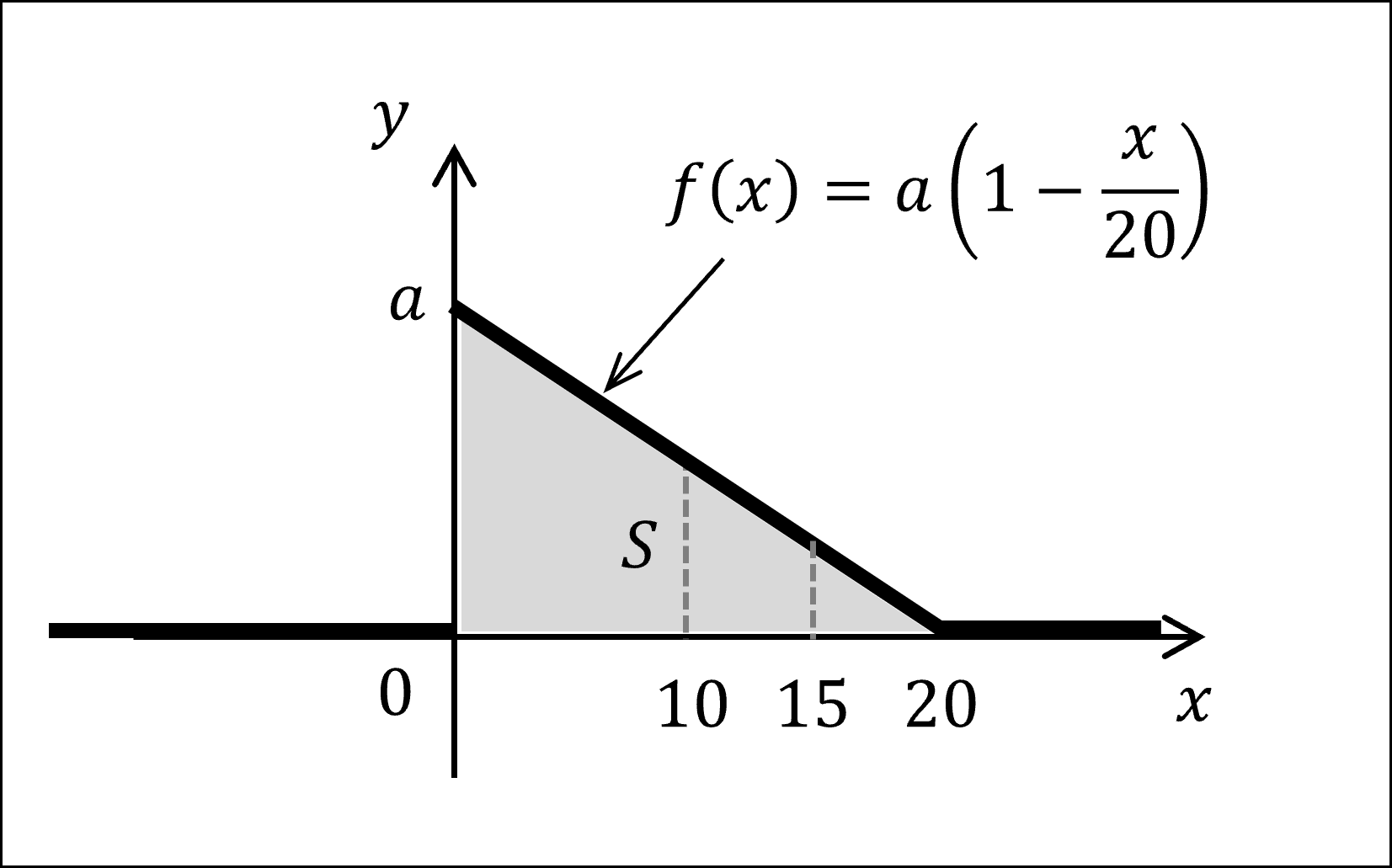
確率密度関数はその下側の面積(確率)が必ず1になります。本問における確率密度関数の下側の面積は上記図のグレーで塗られた部分ですので、この面積をSとおいて以下のようにaの値を導くことができます。
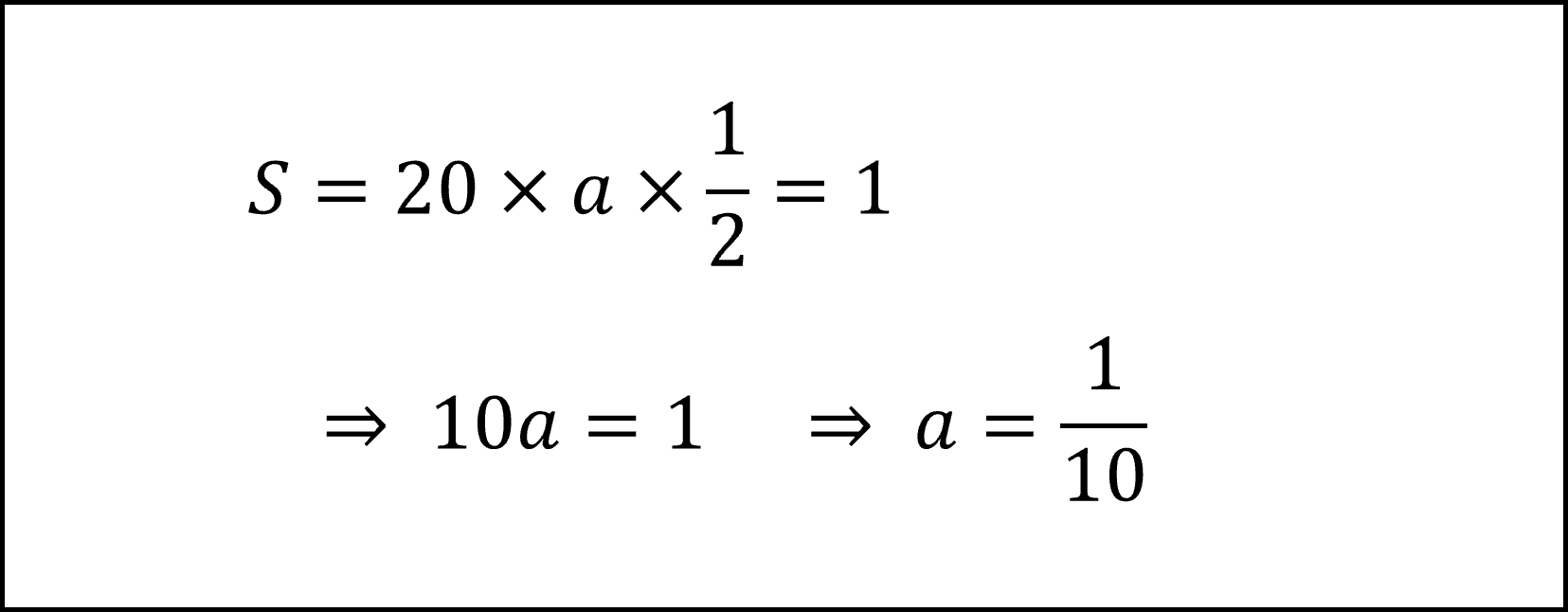
※積分に苦手意識がなければ以下のように積分して1となるように式をおいてaを導いても問題ありません。
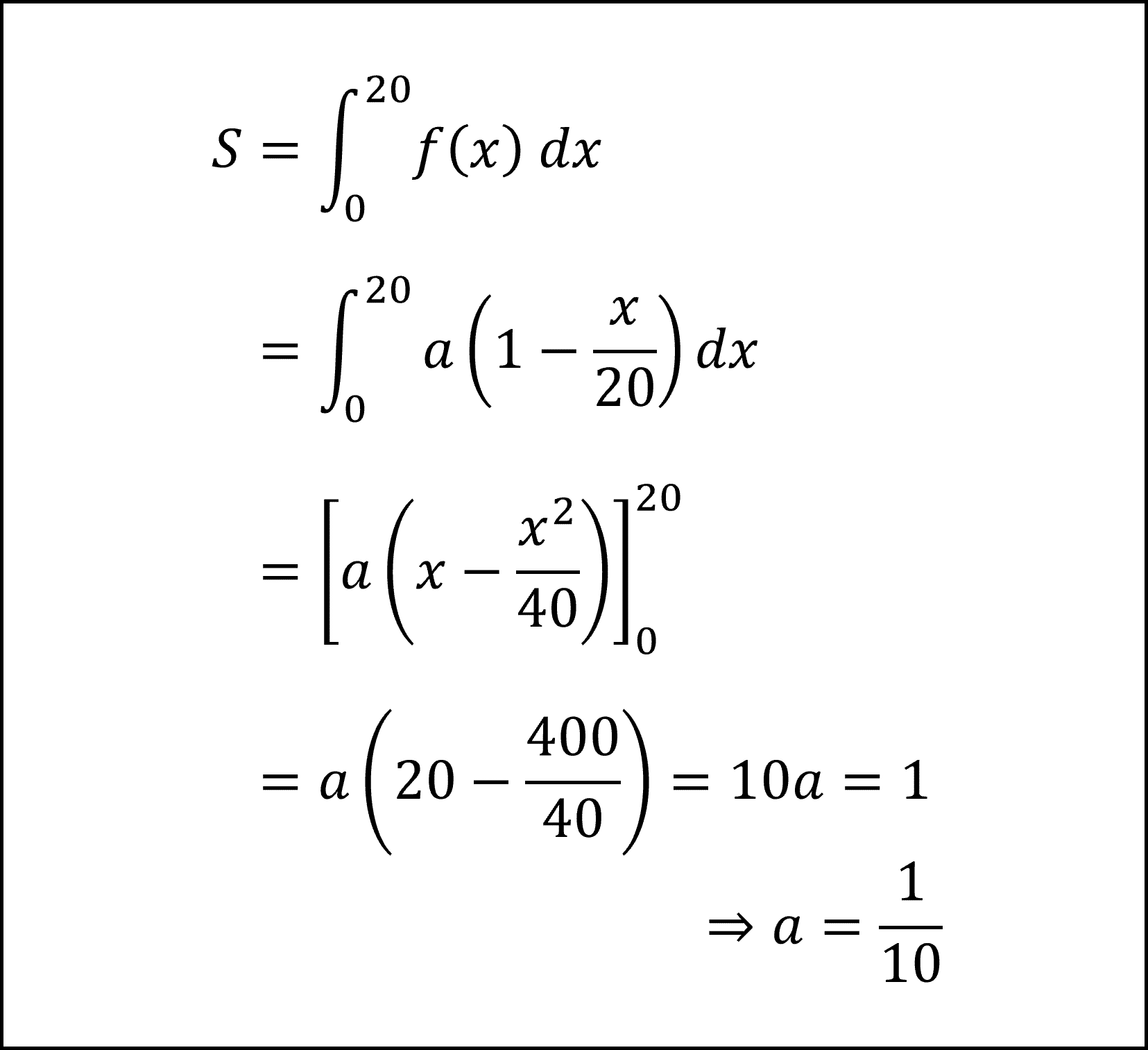
[15番]確率変数 X (水道使用量)の期待値 E[X] は、X を確率(密度関数)で重みづけして計算します。具体的には「x × f (x)」を積分することにより以下のように計算できます。
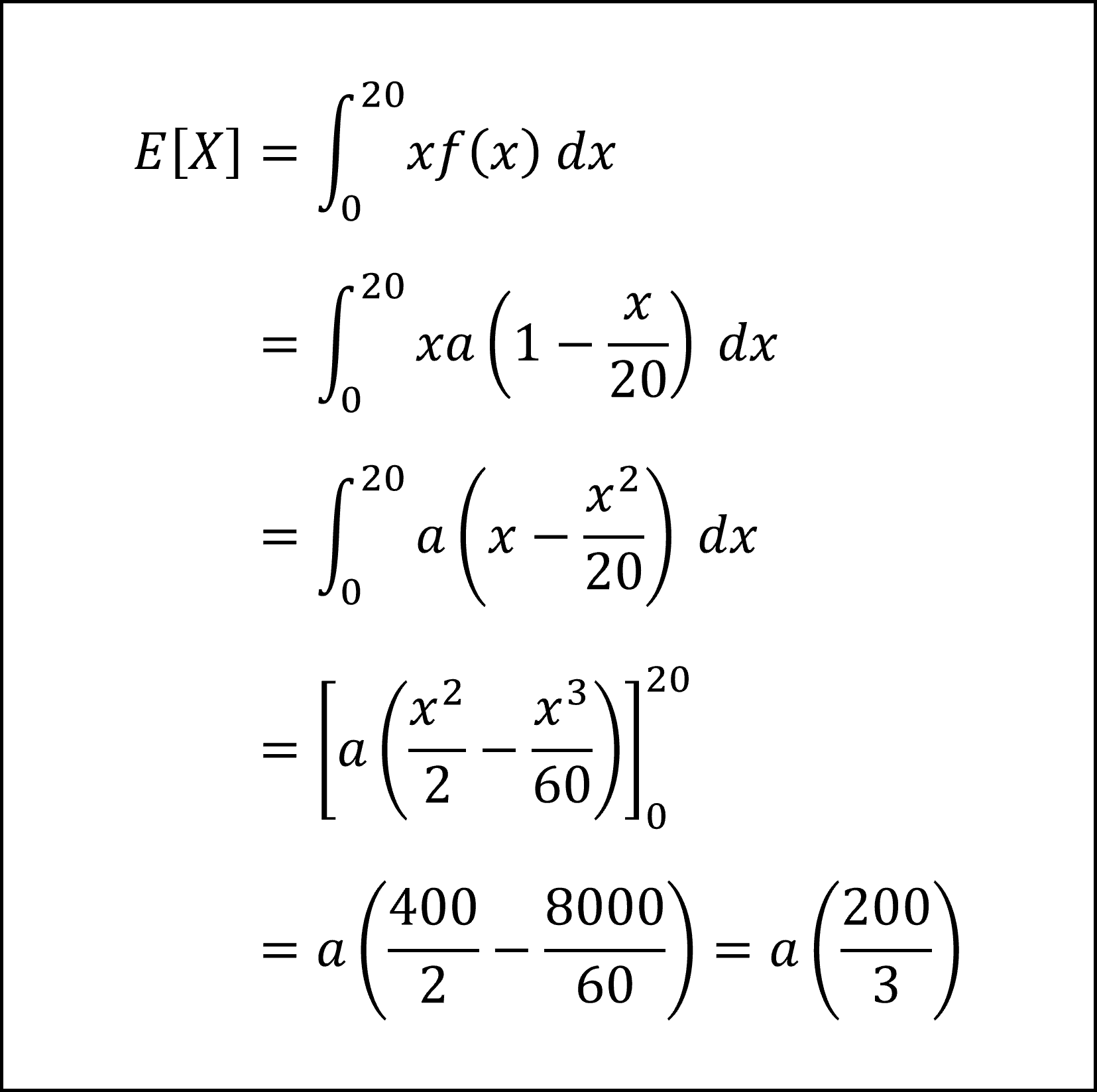
[16番]水道使用「料金」を Y とおいて、その期待値 E[Y] を導きます。
水道使用料金 Y は1,000円(0 ≤ x < 10)、1,120円(10 ≤ x < 15)、1,280円(15 ≤ x)の3つの値を取りうる確率変数です。
3つの値をとる各々の確率を重みとして期待値を計算しますので、3つの値をとる各々の確率をまず計算しましょう。
ア. Y = 1000 (円) となる確率は、0 ≤ x < 10 となる確率ですので、以下のグレーで塗られた面積を求めればよく、
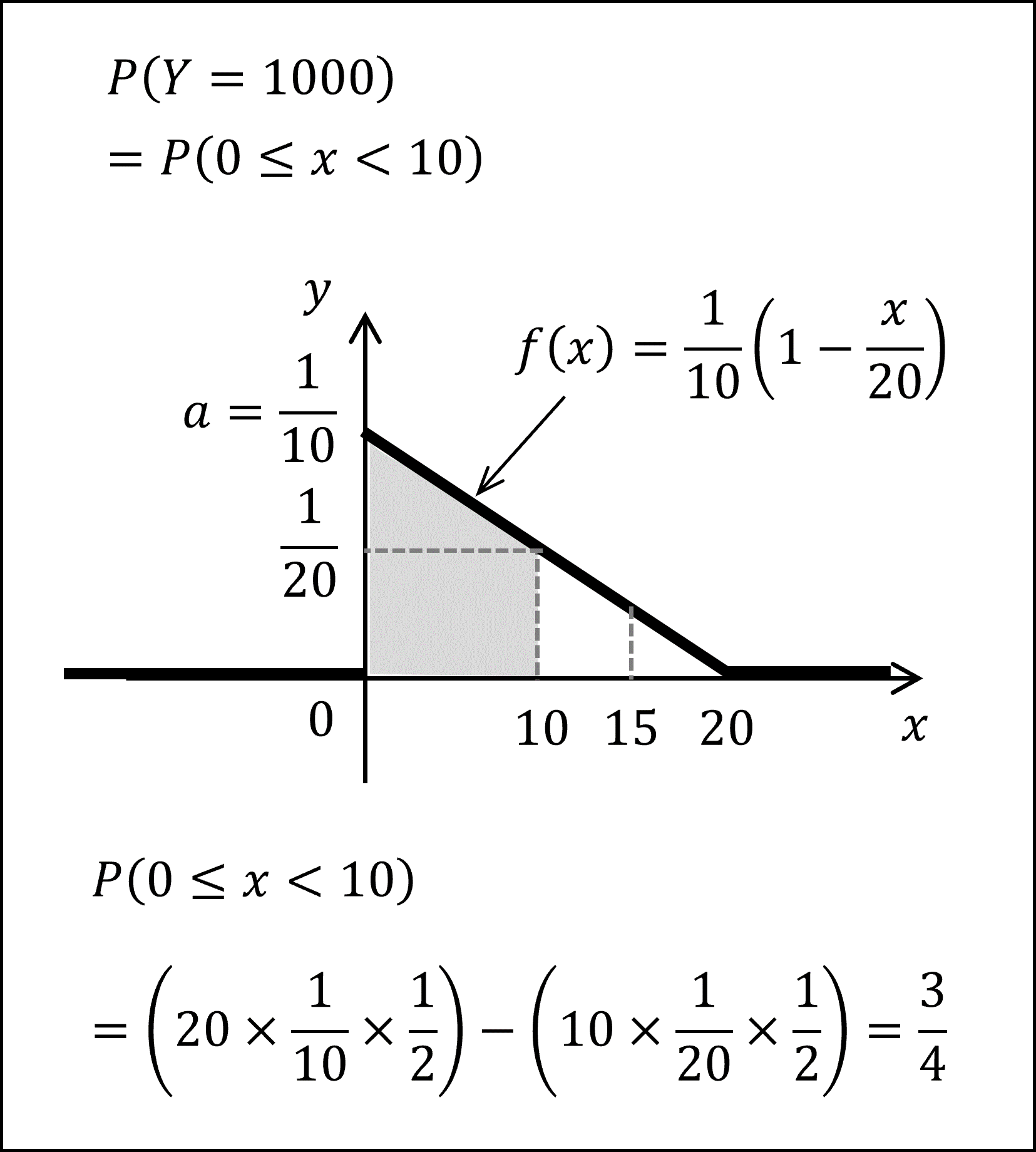
Y = 1000 (円) となる確率は、3/4となります。
イ. Y = 1120 (円) となる確率は、10 ≤ x < 15 となる確率ですので、以下のグレーで塗られた面積を求めればよく、
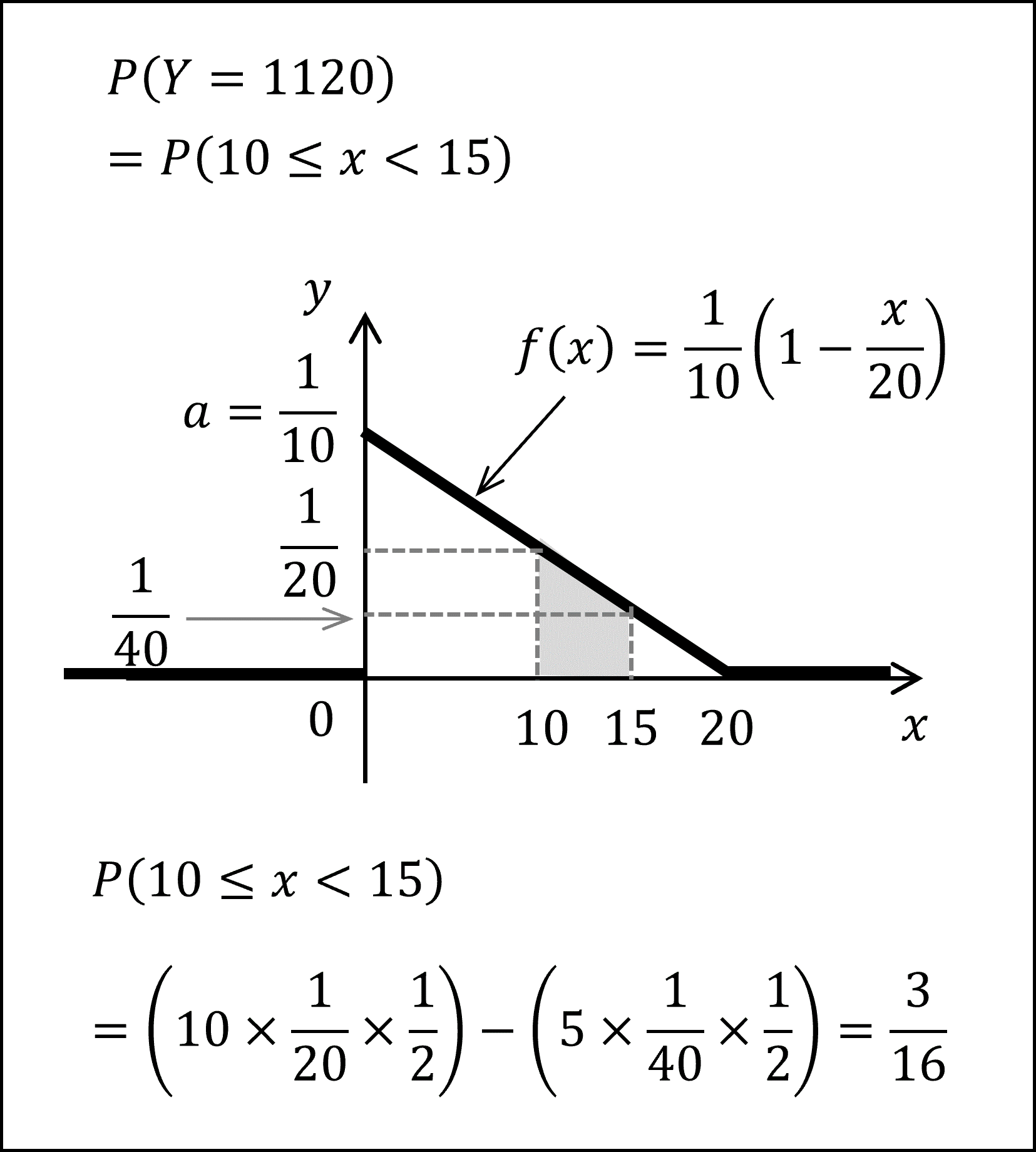
Y = 1120 (円) となる確率は、3/16となります。
ウ. Y = 1280 (円) となる確率は、15 ≤ x となる確率ですので、以下のグレーで塗られた面積を求めればよく、
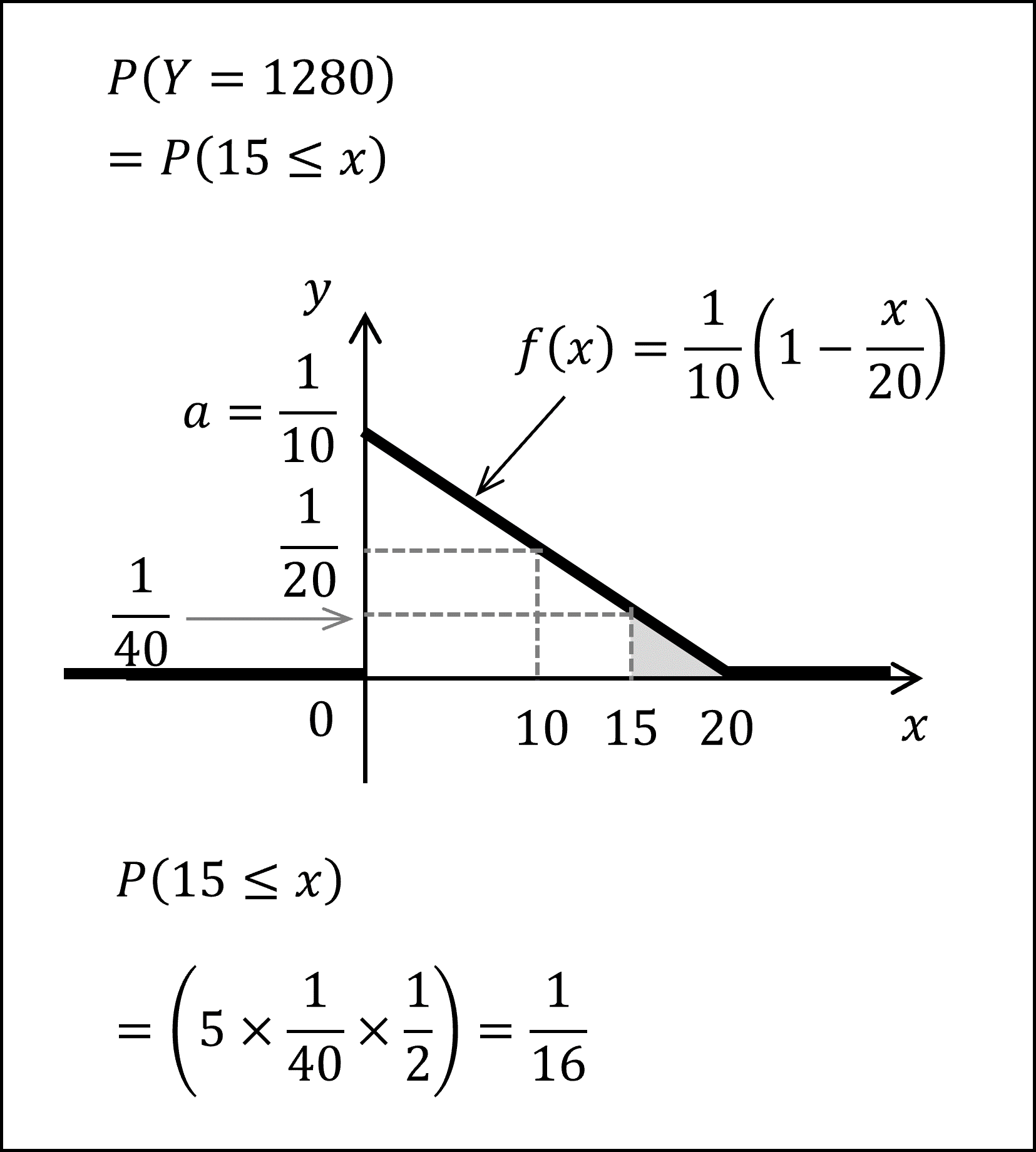
Y = 1280 (円) となる確率は、1/16となります。
以上より「ア. Y=1000(円) となる確率が3/4」「イ. Y=1120(円) となる確率が3/16」「ウ. Y=1280(円) となる確率が1/16」と導けました。
各々の確率を重みとして、以下のようにYの期待値を計算できます。
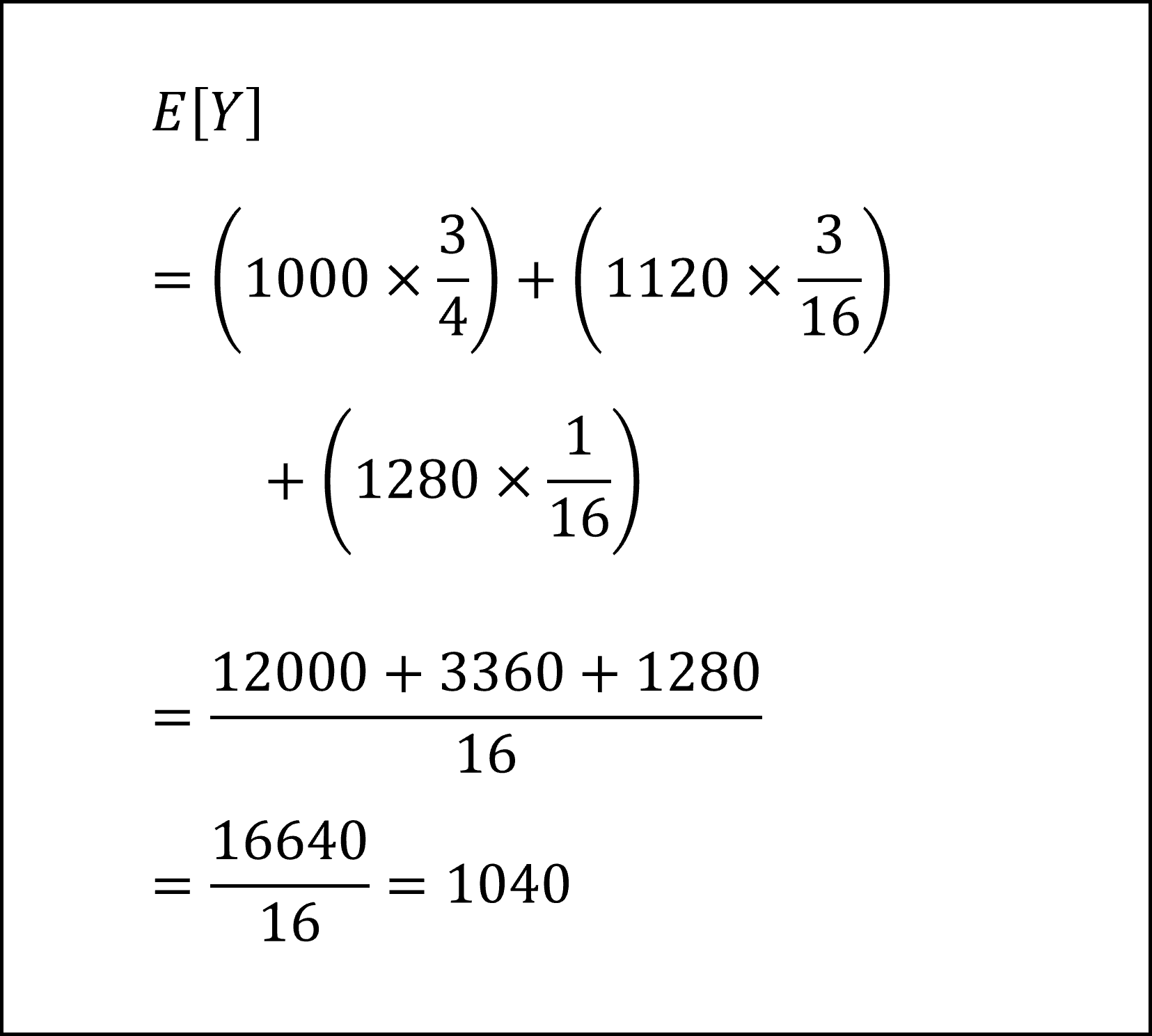
補足
[16番]は難問ですが以下の2つのポイントを理解できていれば正答できそうです。
- (連続型の)確率変数がある区間をとる確率は、確率密度関数の下側の面積である。
- 確率変数の期待値は、確率変数の値を確率で重みづけして計算する。
(例:サイコロの目の期待値は、1×(1/6)+2×(1/6)+…+6×(1/6)=3.5)
(14,15,16番、以上)
問10 [17,18,19番](2019年11月試験)
テーマ
- 分布関数(累積分布関数)
- 下側95%点
- 確率密度関数
- 期待値
正答
[17番]選択肢③ [18番]選択肢② [19番]選択肢②
解答例
[17番]0 ≤ x < 100なる実数 x に対する分布関数の式を導く問題です。分布関数は「確率変数Xが実数x以下となる確率」を表しますので、式で表現すると以下のようになります。
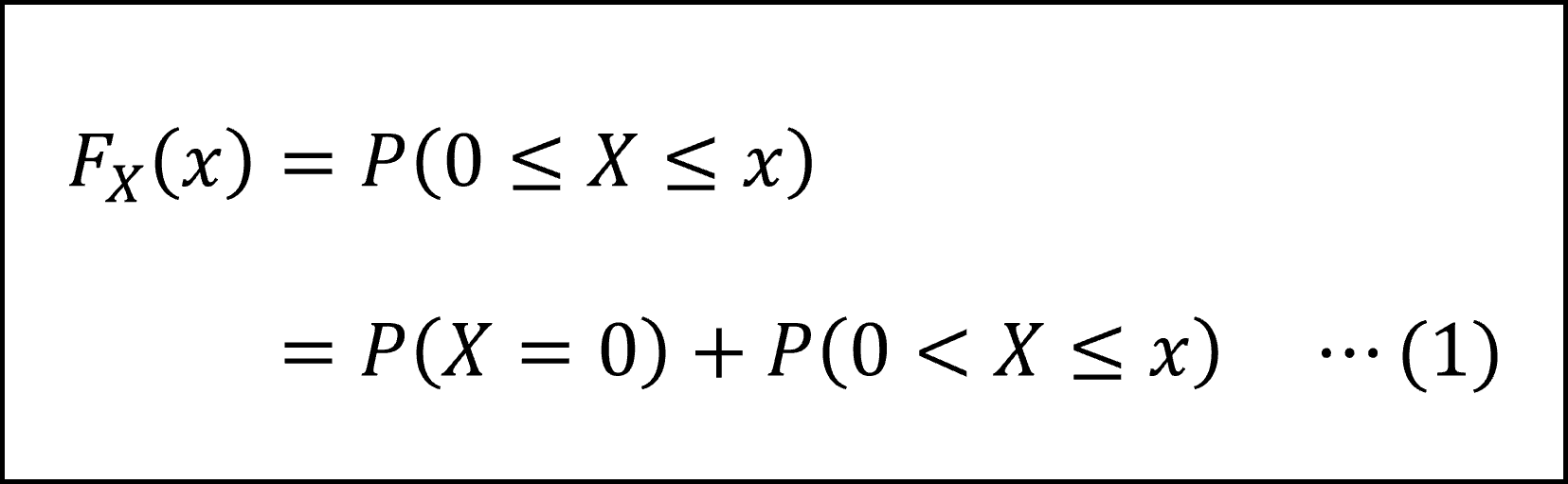
ここで、与えられた条件より、X=0となる確率は、Z > 100となる確率に等しい(※)ので
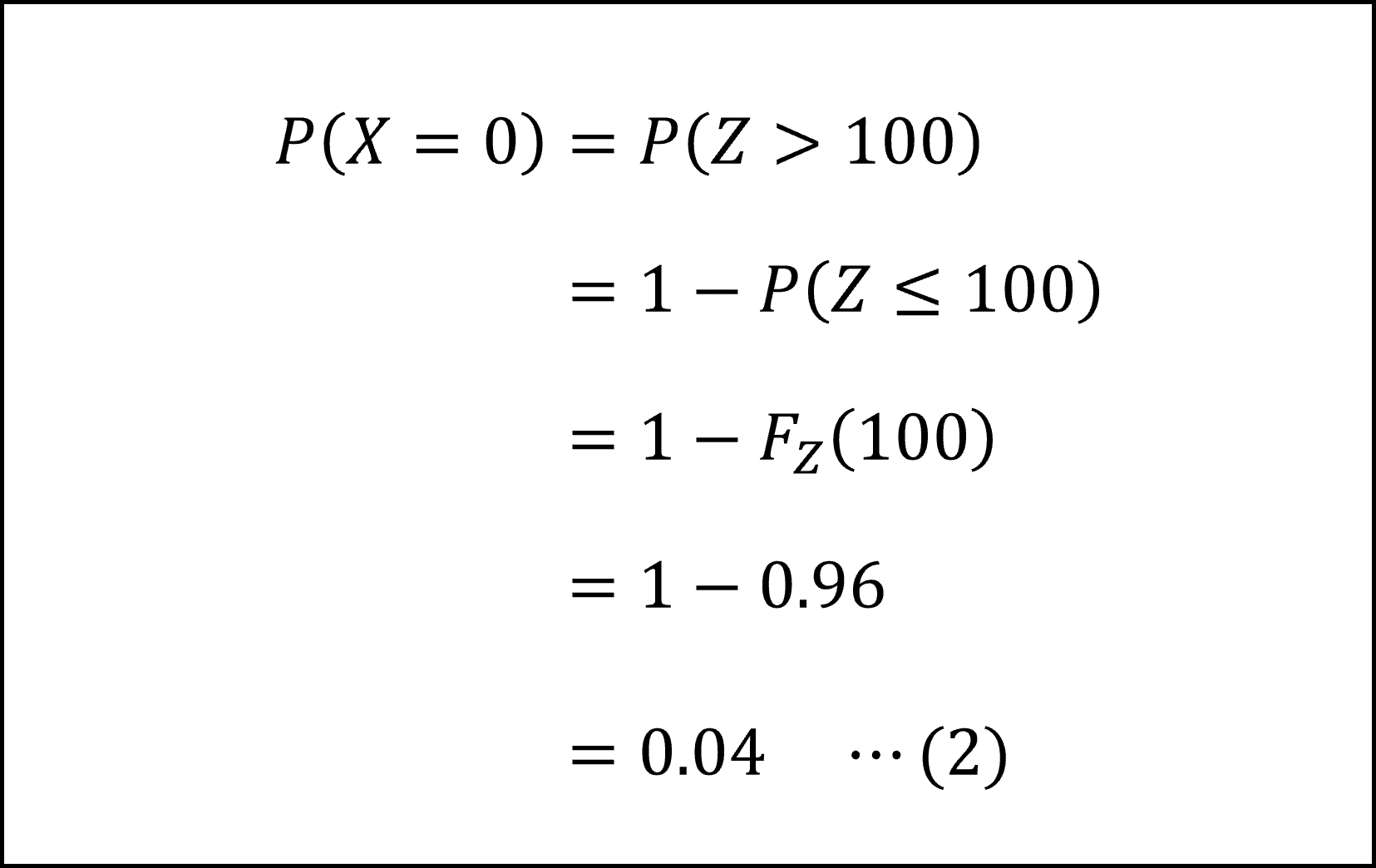
となります。(※:Zは正の値ですので、Z ≤ 100 のときに X(=Z)は0にはなりません。したがって、X=0となる確率は Z > 100 となる確率だけを考えてあげれば大丈夫です)
また、X≠0のときは X=Z(> 0)ですので( x は100より小さい実数という前提にも注意して)
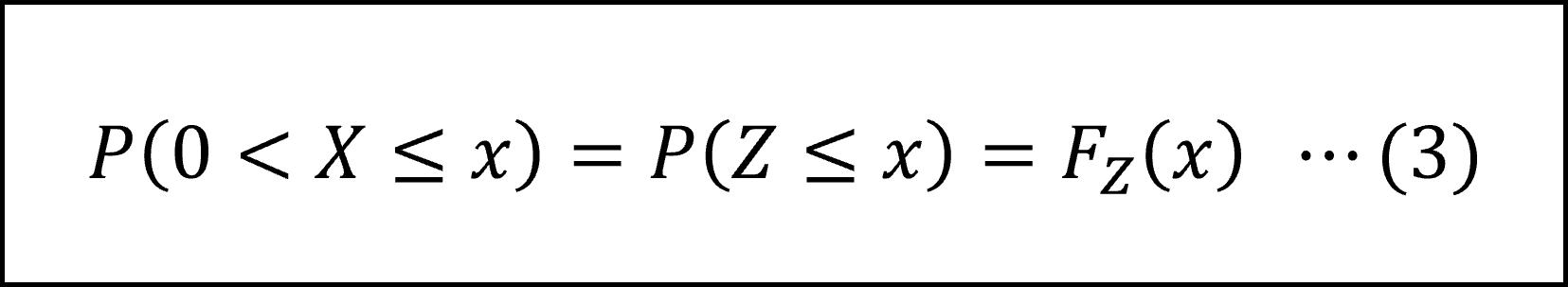
したがって、(1)式に(2)(3)式を代入して以下のように分布関数の式を整理できます。
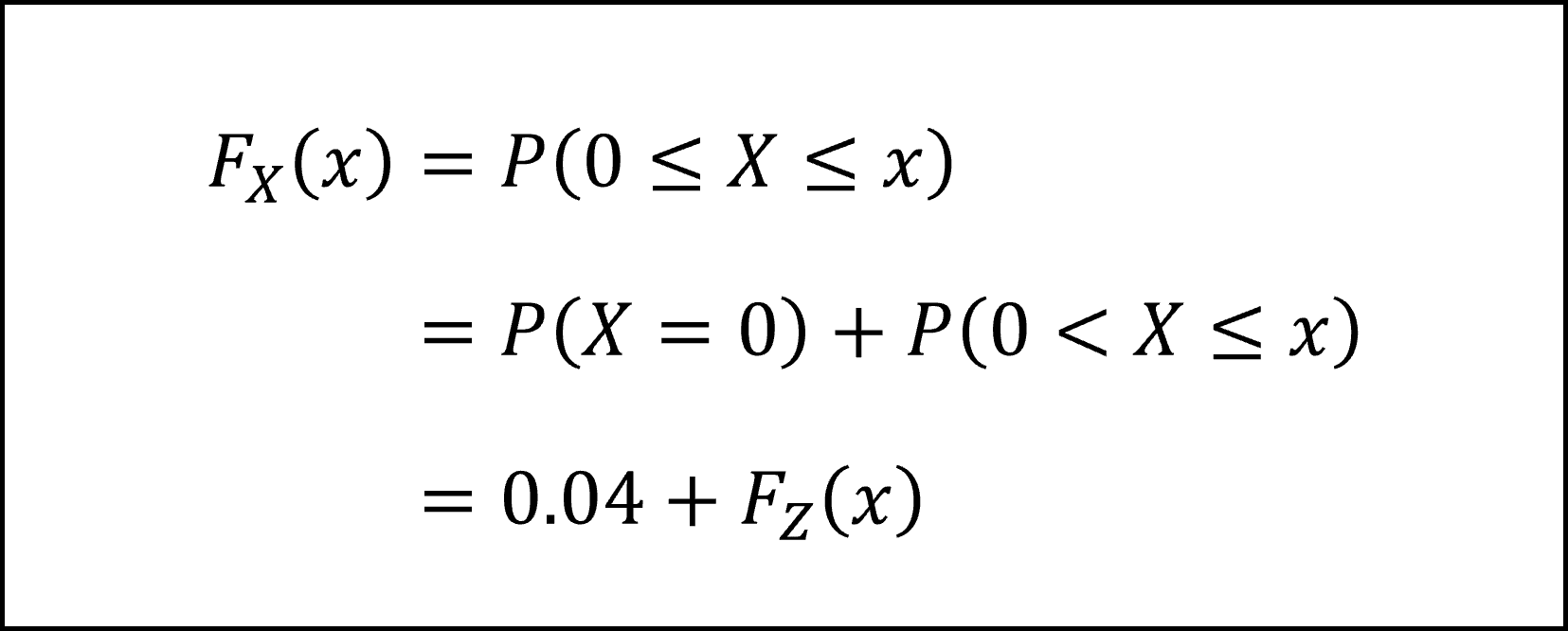
※これはつまり、[ X ≤ x となる確率]=[ Z ≤ x となる確率]+[ X=0となる確率0.04 ]となることを意味しています。
[18番]確率変数 X の下側95%点は「X ≤ x となる確率が95%となるxの値」になります。
「X ≤ x となる確率」というのはまさに[17]で求めた(累積)分布関数で表されるものですので、Xの下側95%点を以下のように導けます。
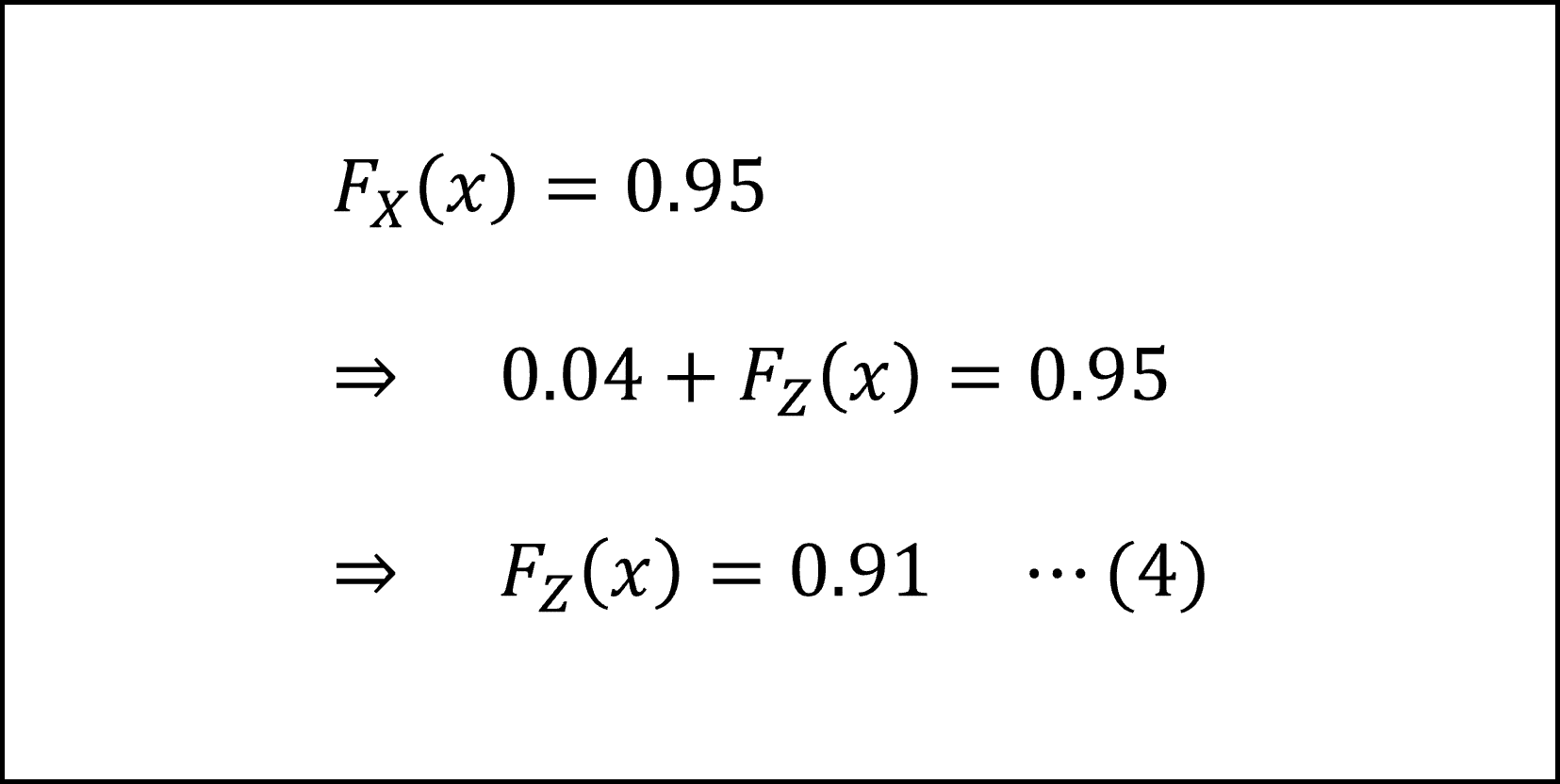
与えられた条件から x=5 のとき(4)式を満たすので、確率変数 X の下側95%点は x=5と導けます。
[19番]確率変数 X の期待値 E[X] は、X を確率(密度関数)で重みづけして計算しますので、以下のような式で表現できます。

ここで、X≠0のときはX=Zですので、
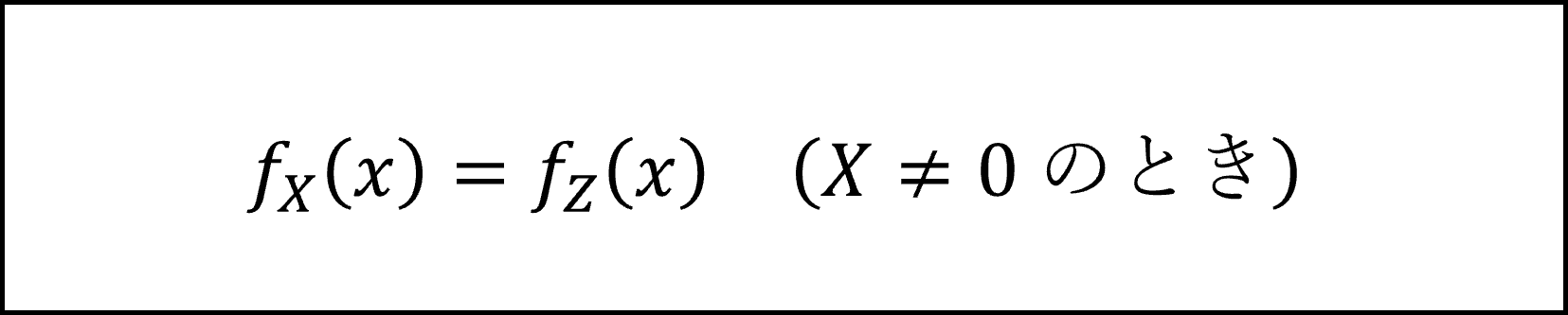
となります。X=0のときの期待値は確率の大きさに関係なく0ですので、期待値の計算においてX=0のときを考慮する必要はありません。
したがって、(5)式を確率変数 Z に関する式に整理しなおして
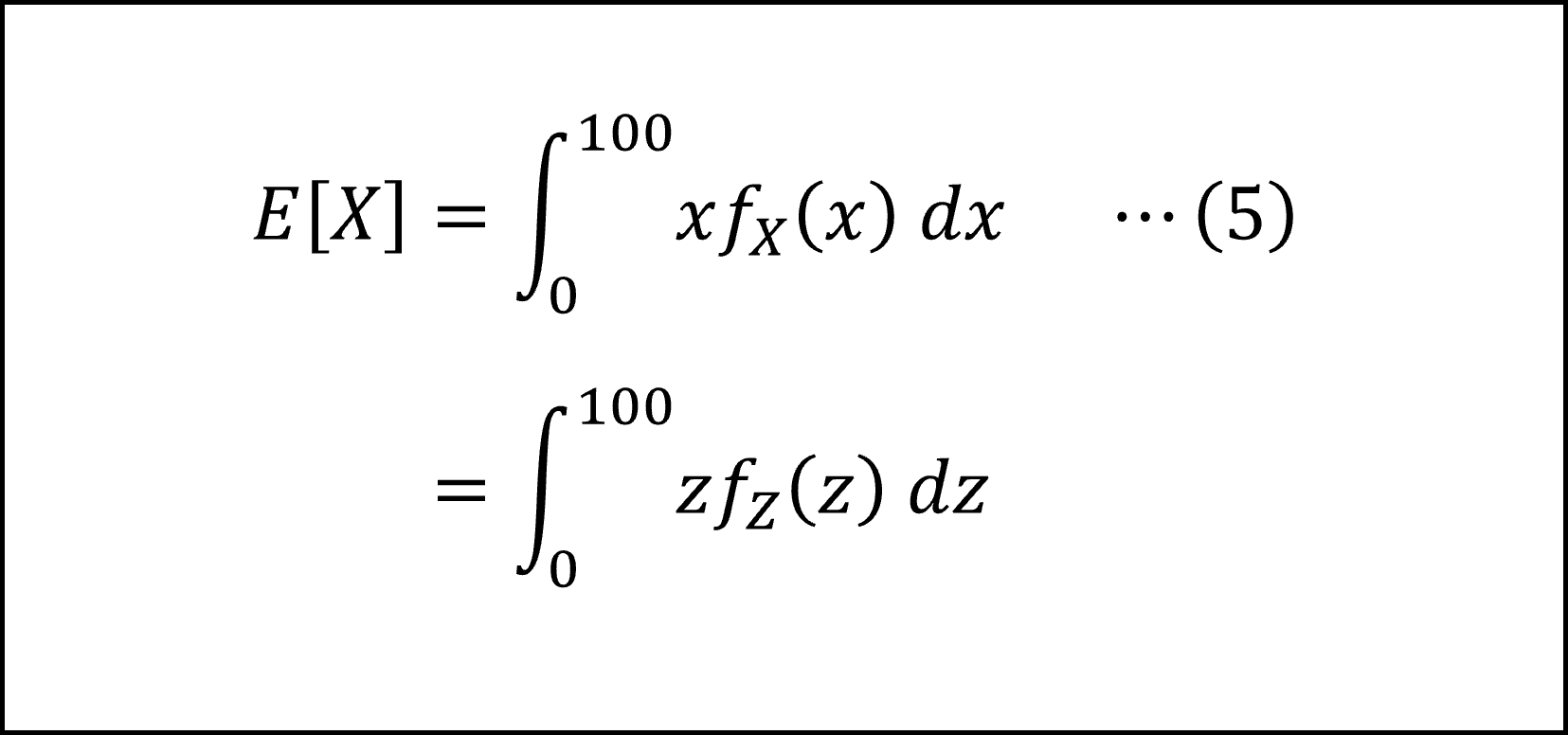
となります。
補足
- 分布関数は確率変数Xの値が実数x以下となる確率であることに注意しましょう。
- なお、問題文の「連続かつ任意の 0 < x < y に対して…」という部分は、分布関数が単調増加(zが増加すれば分布関数も増加)することを意味しており、分布関数の定義を満たしていることを確認する文章になります。
- [19番]については、期待値は「確率変数を確率(密度関数)で重みづけして計算する」という基本に立ち返ることが大切です。
(17,18,19番、以上)

