
※統計検定®は一般財団法人統計質保証推進協会の登録商標です(名称使用の許諾を受けています)。また、本記事は統計検定主催社側から公認されたものではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問01 [01,02,03番](2019年6月試験)
テーマ
- 相対度数分布表
- 平均、中央値
正答
[1番]選択肢③ [2番]選択肢① [3番]選択肢⑤
解答例
[1番] 2008年の貯蓄額「2,000万円以上」の世帯の割合が19.6%で、「2,000万円以上4,000万円未満」の割合が「5.3%+3.8%+4.7%=13.8%」ですので、「4,000万円以上」の割合は「19.6%-13.8%=5.8%」になります。
[2番] 中央値は累積の相対度数が50%となる階級に含まれます。
2015年における700万円未満までの累積の相対度数が「13.2%+7.2%+7.0%+6.1%+5.6%+5.5%+4.5%=49.1%」で、800万円未満までの累積の相対度数が「49.1%+4.2%=53.3%」ですので、「700万円以上800万円未満」の階級に中央値が含まれます。
[3番] 2015年における1309万円未満の世帯の割合を求めます。
2015年における1200万円未満までの累積の相対度数は、[2]で求めた800万円未満までの累積相対度数53.3%を用いて「53.3%+3.3%+3.2%+6.0%=65.8%」になります。また、1400万円未満までの累積相対度数は「65.8%+4.6%=70.4%」になります。
したがって1309万円未満の世帯の割合は「65.8%~70.4%」となりますので、四捨五入すると70%となります。
補足
- 「13.2+7.2+7.0+6.1+5.6+5.5+4.5」のような計算は、小数点もあって電卓を用いてもミスが生じやすい計算です。
- 電卓での計算の1つのコツとして、小数点のボタンを押さずに済むように「13.2+7.2+7.0+6.1+5.6+5.5+4.5=(132+72+70+61+56+55+45)×0.1」と考える方法があります(参考までに)。
問02 [04,05,06番](2019年6月試験)
テーマ
- 散布図
- 相関係数
- 共分散
- 変動係数
正答
[4番]選択肢④ [5番]選択肢② [6番]選択肢②
解答例
[4番] 国語の得点と数学の得点の相関係数は0.72で、比較的強い正の相関があります。国語の得点が高い(低い)ほど、数学の得点も高い(低い)ということなので、散布図は左下から右上にかけて分布します。
選択肢④と⑤が候補になりますが、⑤はほぼ直線上に分布していて相関が強すぎます(0.9くらいでしょうか)ので、正答は選択肢④になりそうです。
[5番] 「相関係数=共分散 / 標準偏差の積」で計算されますので、「共分散=相関係数×標準偏差の積」となります。具体的には以下のように計算できます。
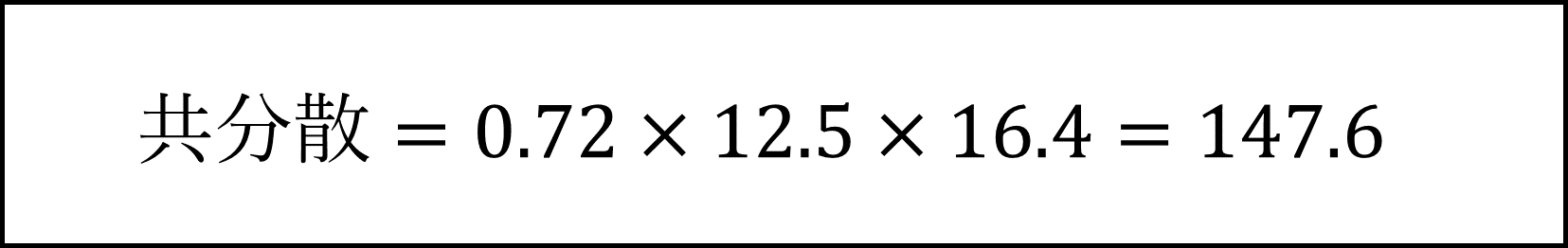
[6番] (A) 変動係数は「平均の値の大きさと比較して変動(標準偏差)がどの程度か」を表す指標で「変動係数= 標準偏差 / 平均」により計算されます。
得点を2倍にすると平均は2倍、標準偏差も2倍(分散は2^2=4倍)になりますので、得点を2倍にした後の変動係数は「(元の標準偏差×2) / (元の平均×2)=元の標準偏差 / 元の平均」となります。したがって、得点を2倍にしても変動係数は変わりません。
(B) 国語の得点を x とし、数学の得点を y 、サンプルサイズを n とすると、国語の得点と数学の得点の共分散(※)は以下の式となります。
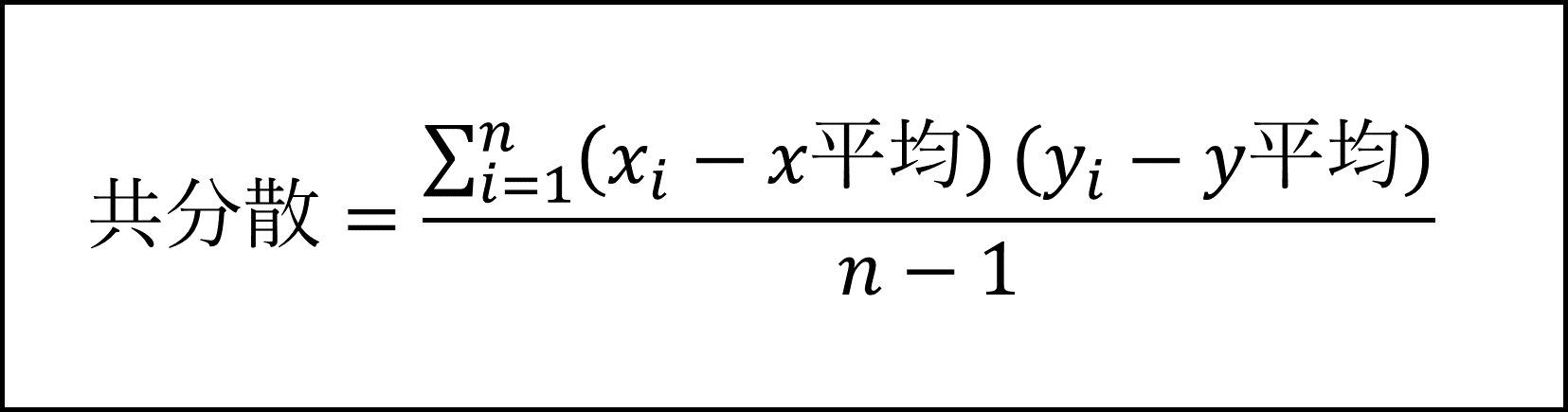
※ここではnではなくn-1で割る不偏共分散としています
ここで、数学の得点yを2倍にすると、

となり、元の共分散の2倍となります。
補足
例えば、身長(体長)について人間の方がアリ(蟻)よりも標準偏差が大きいからと言って、人間の方が身長(体長)のバラツキが大きいと言い切ることには違和感があります。そういったときに「平均の値の大きさと比較してバラツキがどの程度か」を測れる変動係数が用いられます。
問03 [07,08番](2019年6月試験)
テーマ
- 標準化
- 標準化得点
正答
[7番]選択肢④ [8番]選択肢④
解答例
[7番] 《記述Ⅰ》問題文に与えられた以下の式
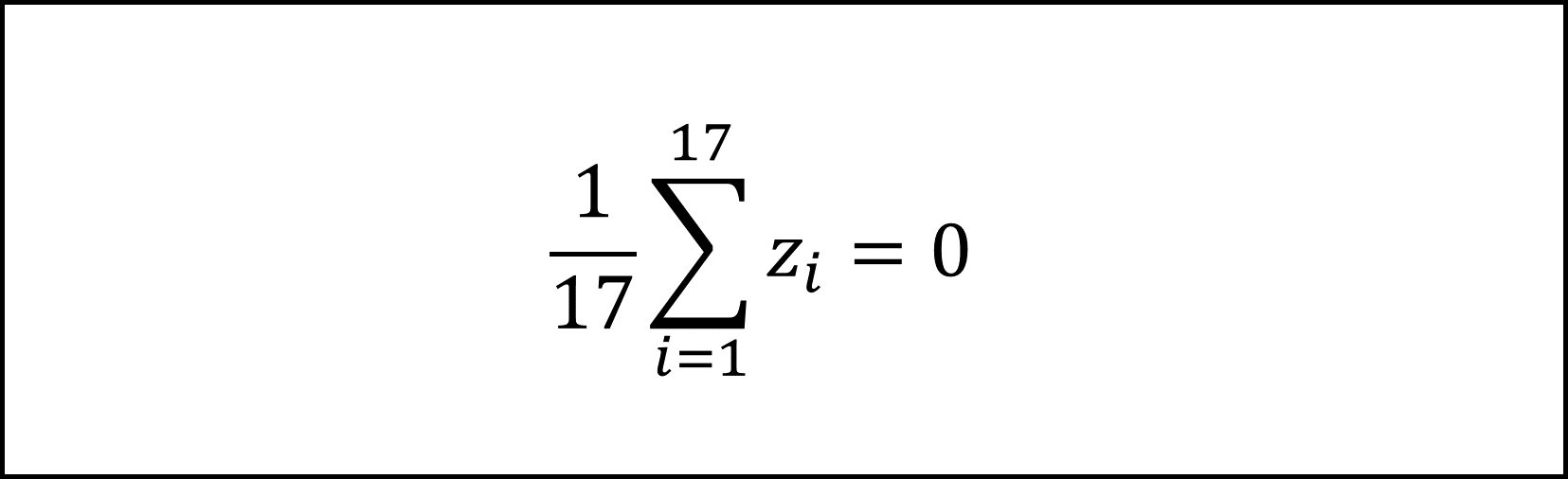
の左辺は、摂氏の値を標準化した標準化得点zの平均を表す式です。標準化得点zの平均は0ですので、上記の式は正しいです。
また、問題文に与えられた以下の式
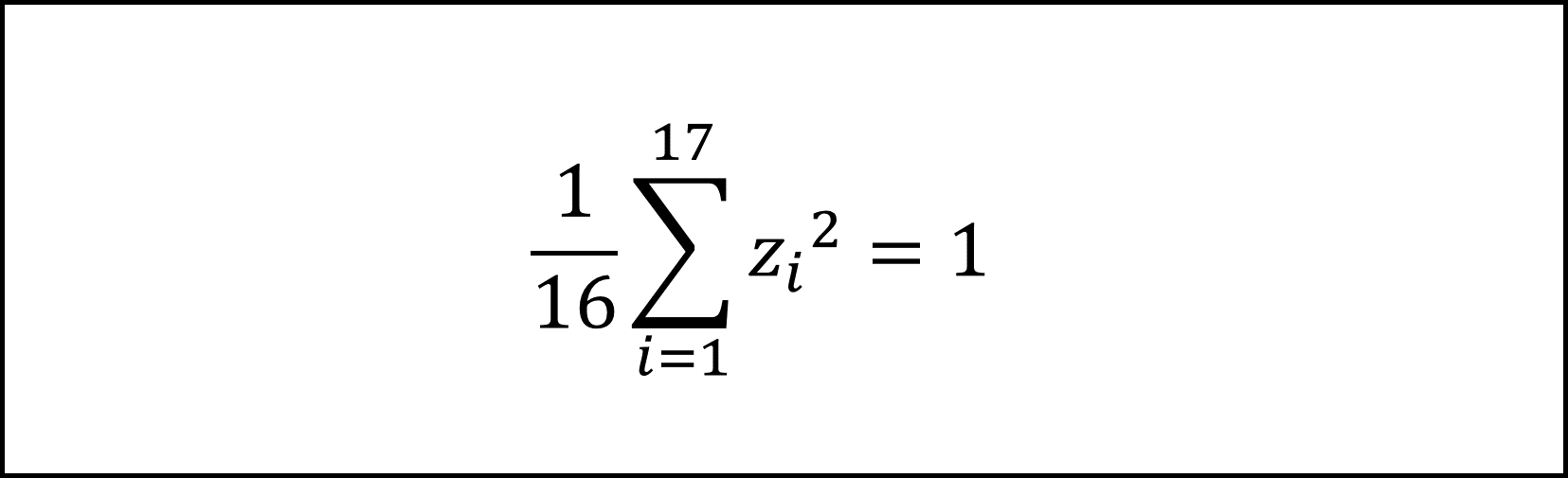
の左辺は、標準化得点zの不偏分散を表す式です。標準化得点zの不偏分散(および標準偏差)は1となりますので、上記の式は正しいです。
《記述Ⅱ》標準化得点zは平均0、標準偏差1です。したがって「zの値が2.5(=標準偏差×2.5倍)よりも小さい」ということは、「値が平均から標準偏差の2.5倍を足した値よりも小さい」と読み替えることができます。
標準化する前の元々の平均は2.4、標準偏差は7.0ですので、標準化する前の値が「2.4+(7.0×2.5)=19.9よりも小さい」かどうかを確認すればOKです。表の摂氏の値を確認すると「No.14 マイアミ」の値が22で19.9よりも大きくなっていますので、記述Ⅱは「誤り」です。
《記述Ⅲ》問題文よりF=1.8C+32ですので華氏Fの平均は(華氏Fの各都市の値をFi、平均をFバー、また、摂氏Cの各都市の値をCi、平均をCバーとして)
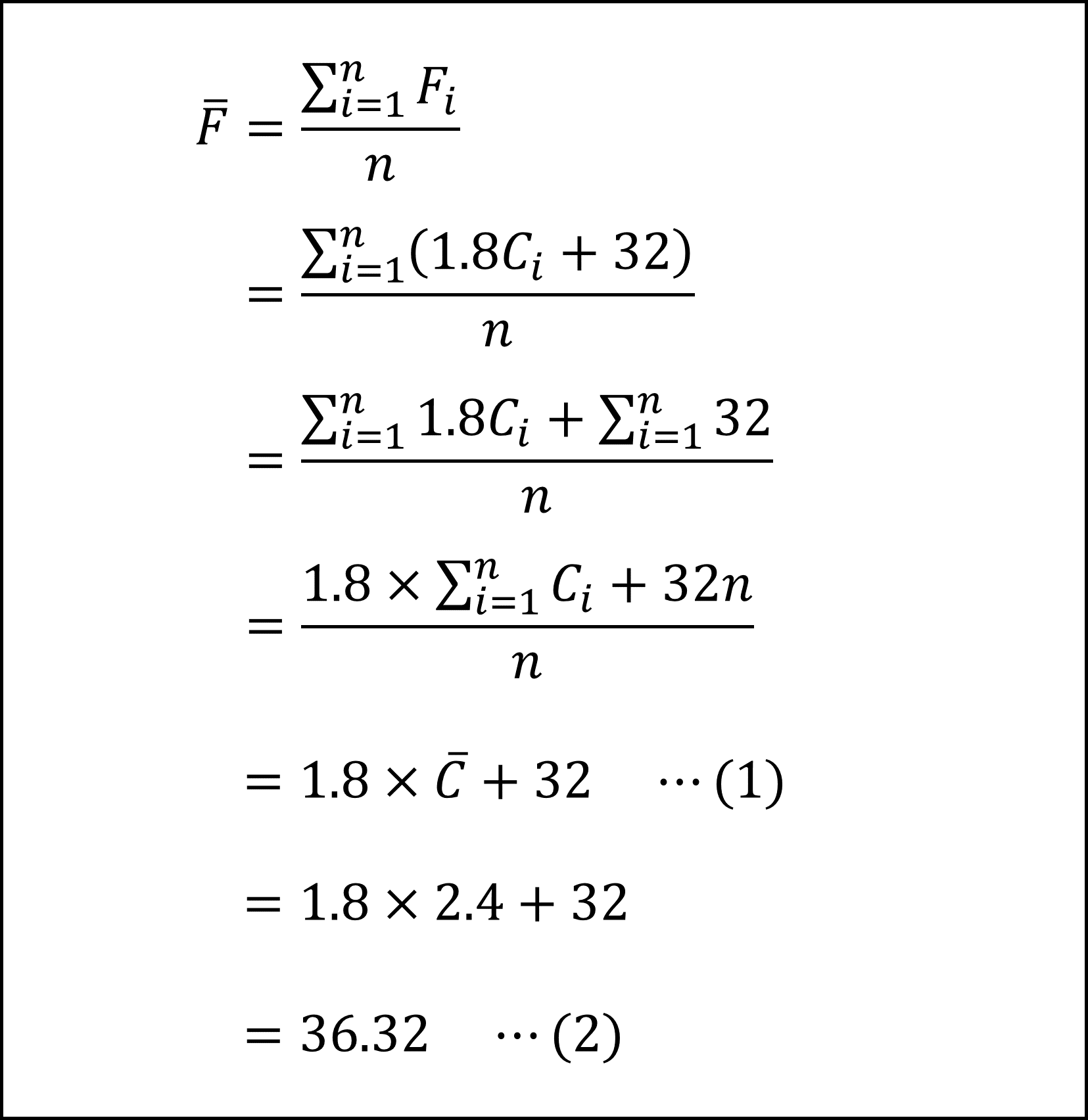
となります(簡単に言うと摂氏Cの平均を1.8倍して32を足せば華氏Fの平均になります)。
また、華氏Fの標準偏差は
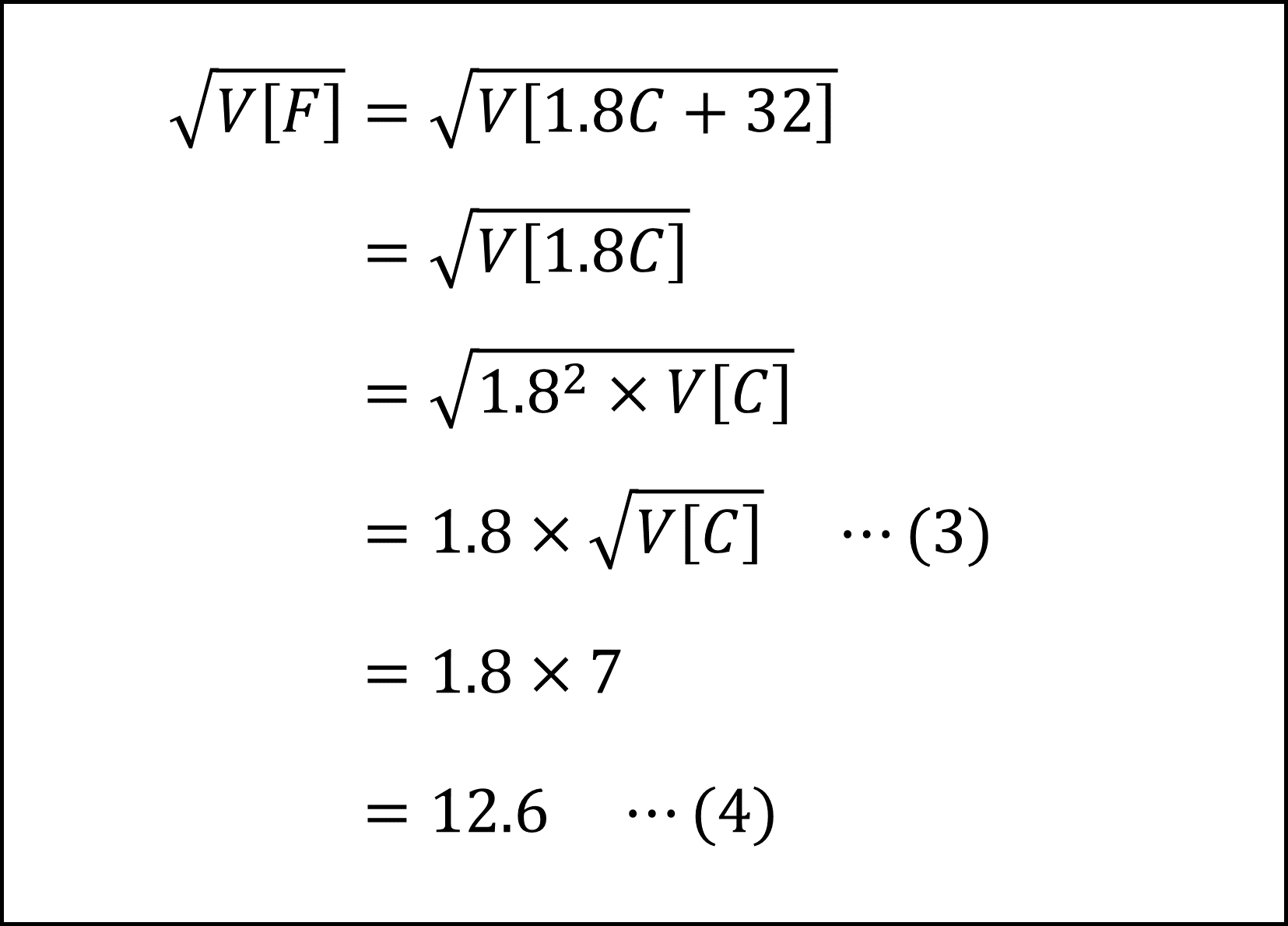
となります(簡単に言うと摂氏Cの標準偏差を1.8倍すると華氏Fの標準偏差になります)。
華氏Fの標準化得点wは上記の(1)式、(3)式を用いて、
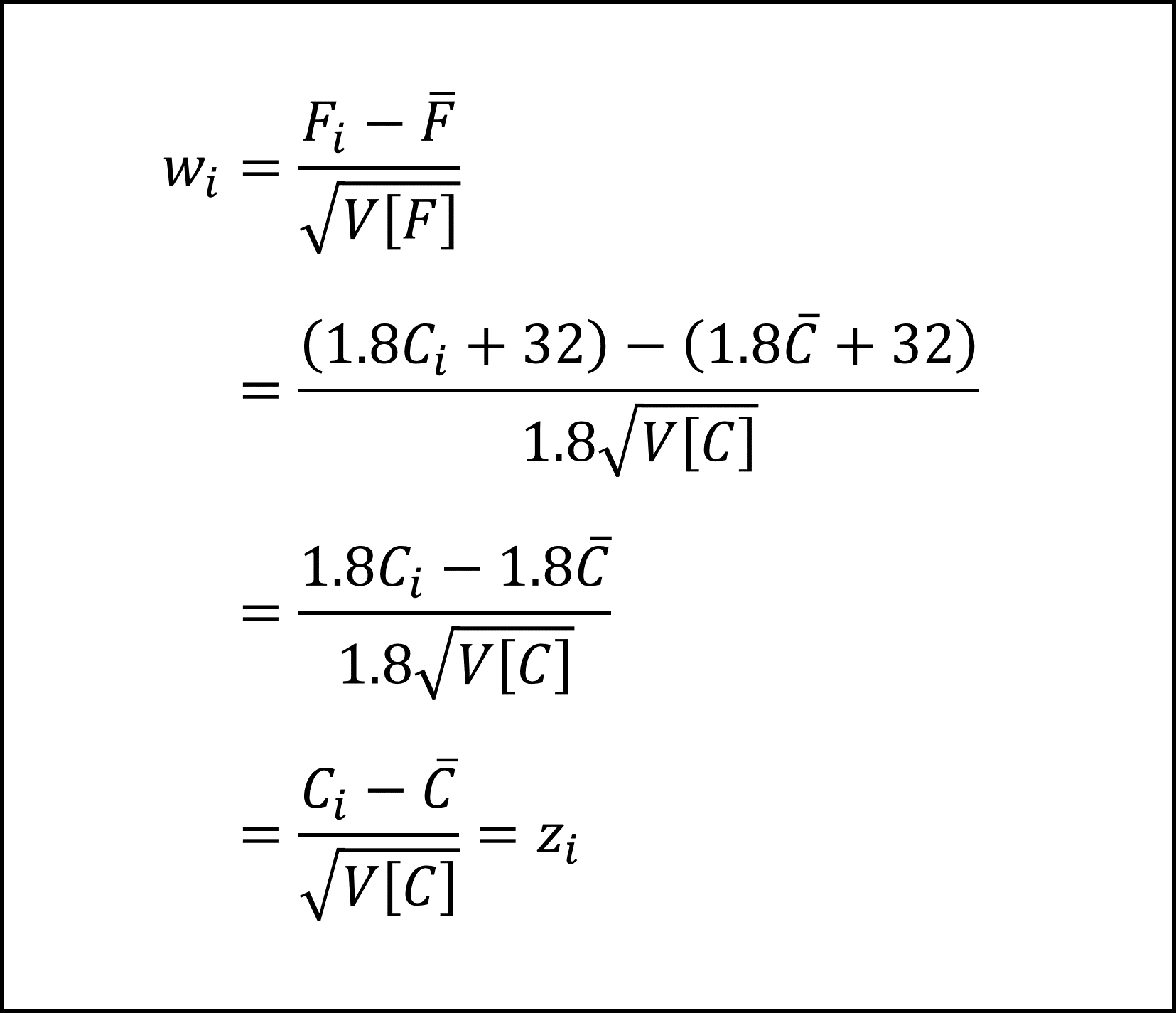
となり、w=zとなりますので記述Ⅲは「正しい」です。
[8番] [7番]で導いた(2)式と(4)式より、華氏Fの平均は約36.3、標準偏差は12.6となります。
補足
- Y=aX+bという関係(1次変換の関係)がある場合、YはXの分身のようなものだと考えるとわかりやすいかと思います。
- 標準化得点は平均が0ですので、標準化得点の値(の絶対値)そのものが「標準偏差の何倍だけばらついているか」を表してくれます。標準化得点が1.5なら標準偏差の1.5倍だけばらついた値ですし、標準化得点が2.4なら標準偏差の2.4倍だけばらついた値となります。
問04 [09,10番](2019年6月試験)
テーマ
- 相関係数
- 偏相関係数
正答
[09番]選択肢① [10番]選択肢③
解答例
[09番]《記述Ⅰ》相関係数が0.91と非常に大きいので、世帯人員が多ければ(少なければ)持家率が高い(低い)という正の相関関係(散布図を描くと右肩上がりの直線となるような関係)が認められます。よって「正しい」です。
《記述Ⅱ》偏相関係数も相関係数と同様に線形な関係を捉えるものですので「誤り」です。
《記述Ⅲ》相関係数が正なら偏相関係数は負になるとは限りませんので「誤り」です。
[10番] 《記述Ⅰ》相関係数や偏相関係数はあくまでも「変数全体」を通じての関係性を表現するものです。したがって、「収入の水準が上昇すると」とか「高収入の世帯ほど」など、収入の水準によって相関係数そのものが変化するという内容は「誤り」です。
《記述Ⅱ》相関係数や偏相関係数はあくまでも「変数全体」を通じての関係性から具体的な値に決まります。したがって、収入の水準が変動すると相関係数そのものが変動するという内容は「誤り」です。
《記述Ⅲ》「正しい」内容です。
「収入の影響を除去」することで、第3の共通因子として収入が背後で影響を与えている分(擬相関)を除去します。除去する前の相関係数が0.91で除去した後の相関係数(偏相関係数)が0.79ですので、0.12だけ小さくなっています。これは、収入が共通因子として影響を与えていた分が存在していたためと考えられます。
補足
- 偏相関係数は「第3の共通因子の効果を除外した相関係数」です。
- 「偏」というのは英語でpartialです。「部分的な相関係数」とか「断片的な相関係数」とか「第3因子の影響を”そぎ落とした”相関係数」などとイメージするとわかりやすいかと思います。
問05 [11番](2019年6月試験)
テーマ
- フィッシャーの3原則
- 無作為化
- 繰り返し
- 局所管理
正答
選択肢①
解答例
《記述Ⅰ》「無作為化」は実験の処理条件を無作為(ランダム)に割り付けることで不要な偏り(バイアス・系統誤差)を偶然誤差に転嫁しようとするものです。よって「正しい」内容です。
《記述Ⅱ》「繰り返し」は実験を繰り返すことでデータの変動(ばらつき・偶然誤差)の大きさを見積もろうとするものです。同一の実験条件に複数の被験者を割り当てることで、被験者の違いによる変動(ばらつき・偶然誤差)の大きさを見積もることができ、これも「繰り返し」に該当します。よって「誤り」です。
《記述Ⅲ》「局所管理」は実験の場をなるべく均一な条件のブロックに分けることで、処理効果以外の偏り(バイアス・系統誤差)をなるべく小さくしようとするものです。実験を監督・監視する人を割り付けることを意味するものではありません。よって「誤り」です。
補足
- 「フィッシャーの3原則」のポイントは偶然誤差(分散・ばらつき)と系統誤差(偏り・バイアス)です。
- 「無作為化」は不要な系統誤差を偶然誤差に転嫁しようとするものです。
- 「繰り返し」は偶然誤差の大きさを見積もろうとするものです。
- 「局所管理」は処理効果以外の系統誤差が紛れ込むのを防ごうとするものです。
問06 [12番](2019年6月試験)
テーマ
- 多段抽出
- 系統抽出
- 単純無作為抽出
- クラスター(集落)抽出
正答
選択肢⑤
解答例
多段抽出は段数を増やすほど標準誤差(標本統計量の標準偏差)が大きくなり、推定精度が低くなります。よって①は「誤り」です。
系統抽出は、まず母集団の要素に通し番号をつけて、次に無作為にスタート地点を選び、そしてそのスタート地点から等間隔に標本を抽出します。母集団をグループ分けするわけではなく②は「誤り」です。
回答率の低い調査の場合、回答者バイアス(回答した人にのみ生じる偏り)が懸念されるため、有効回答数が多かったとしても、高い精度を達成できるとは言い切れません。よって③は「誤り」です。
系統抽出は系統(抽出間隔)に規則性があった場合など、標本に偏りが生じてしまい推定精度が低くなります。よって④は「誤り」です。
正答は⑤です。クラスター抽出のポイントは抽出されたクラスター(集落)内のすべての個体を調査するという点です。
補足
- 系統抽出は英語ではSystematic samplingで、こちらの方が腹落ちしやすいと思います。
問07 [13番](2019年6月試験)
テーマ
- 排反事象
- 独立事象
正答
選択肢②
解答例
事象Aと事象Bが互いに相反する事象であるときを「排反」と言い、その定義は以下のようになります。
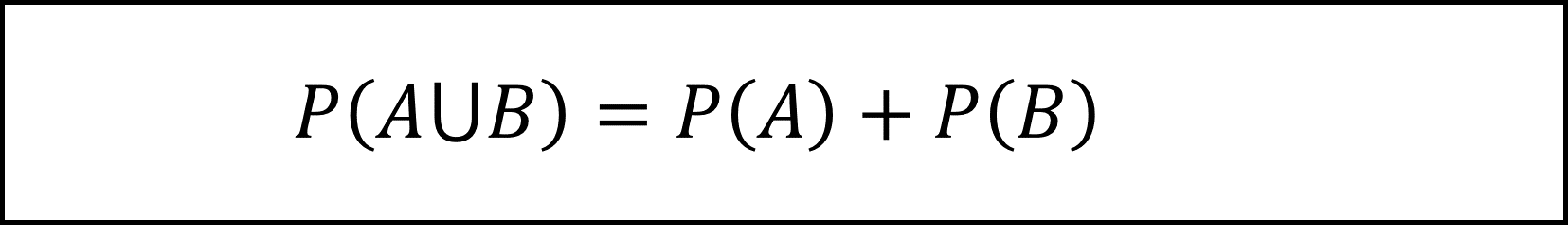
また、排反でないときは事象Aと事象Bの和集合の確率P(A∪B)は以下の式になります。
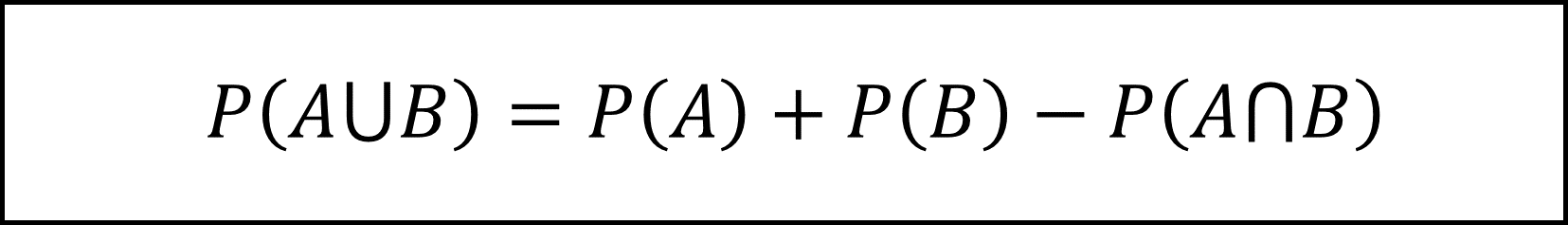
問題文より
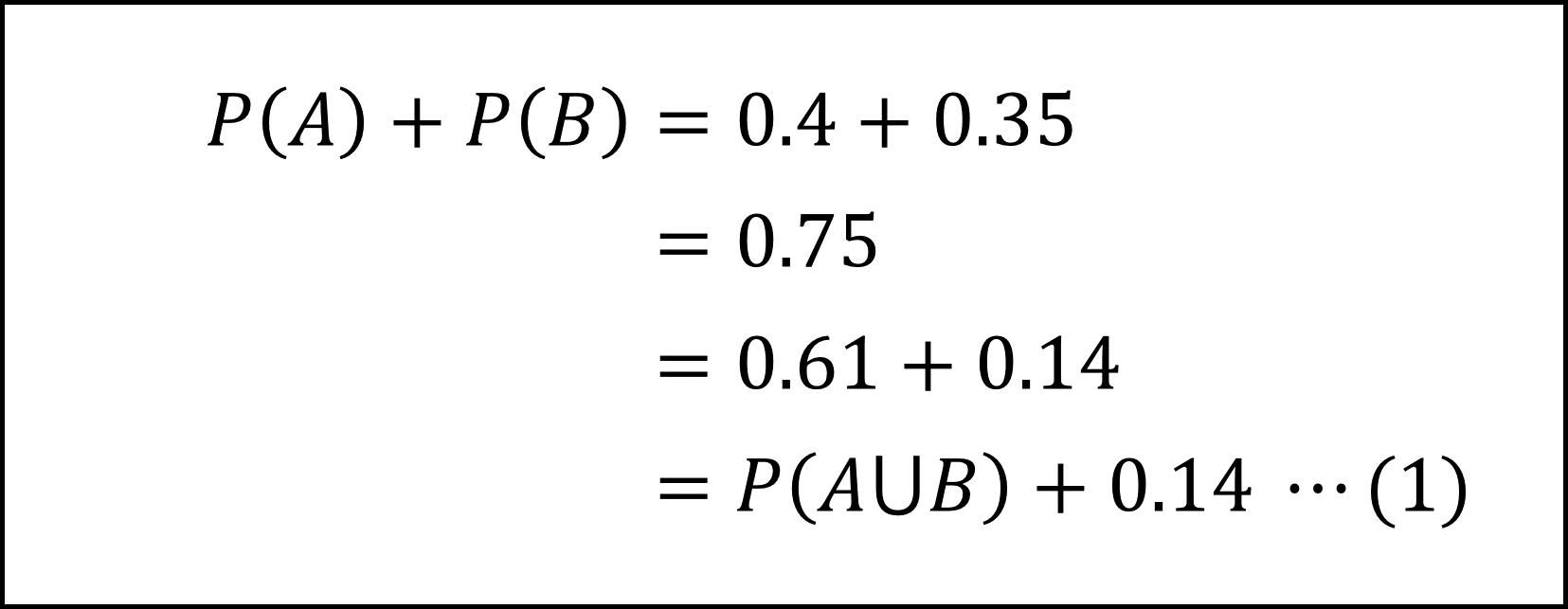
となりますので事象Aと事象Bは排反の定義を満たしません。
また、事象Aと事象Bが独立な事象のときの定義は以下のようになります。
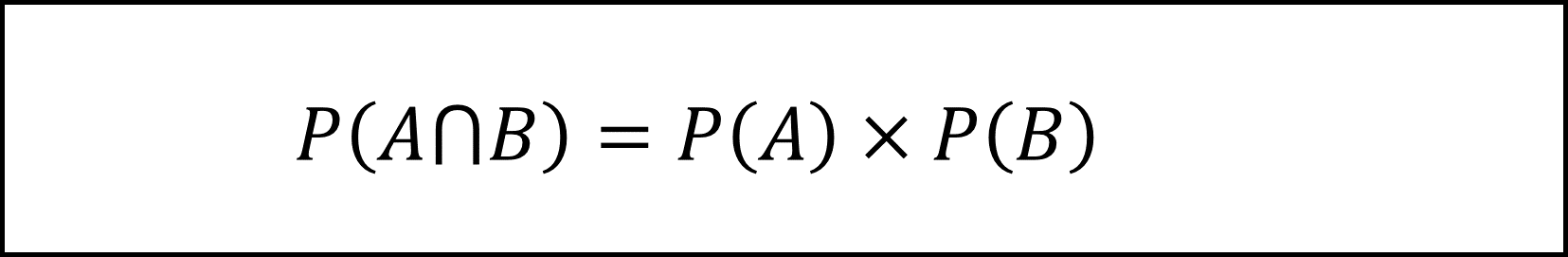
(1)式よりP(A∩B)は0.14であり、これはP(A)×P(B)=0.4×0.35=0.14と等しいので、独立性の定義を満たします。よって事象Aと事象Bは独立です。
したがって②が正答になります。
補足
- 排反かどうかはベン図を描くと分かりやすいです。互いの事象の領域が重複しないような場合を排反といいます。
- 独立かどうかは意外とイメージしづらいので注意しましょう。自分で覚えやすい例を1つ作っておくと良いかと思います。
(例1)2個のサイコロの目が偶数となるという事象は、2個のサイコロを同時に振っても(P(A∩B))、片方を振った後にもう片方を振っても(P(A)×P(B))、その確率は同じである(=独立な事象)。
問08 [14,15番](2019年6月試験)
テーマ
- 条件付き確率
正答
[14番]選択肢⑤ [15番]選択肢⑤
解答例
[14番] 以下の式により計算できます。
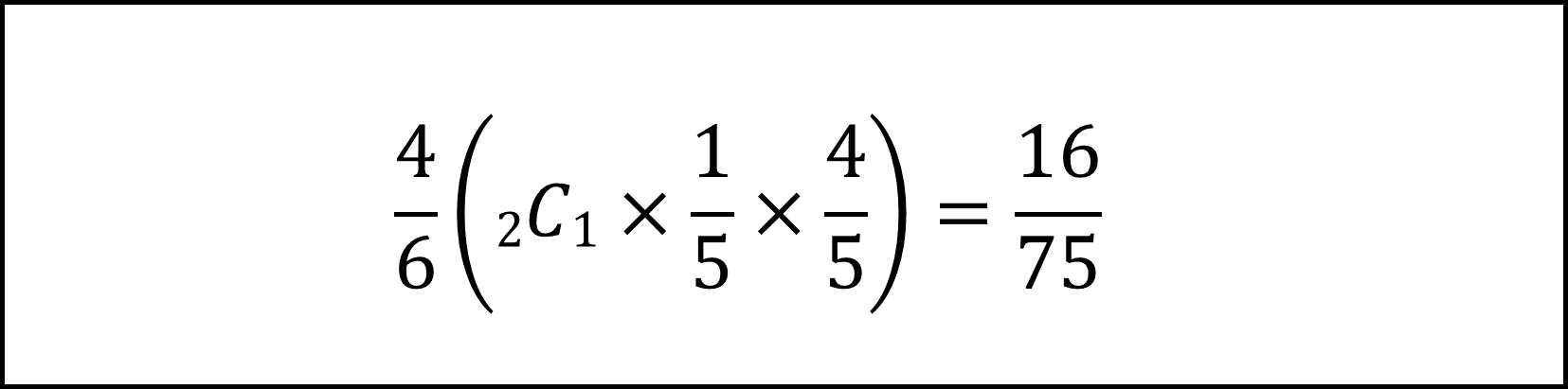
[15番] Xの期待値E[X]を計算するためには、Xが各値(0,1,2)をとる確率をまず導く必要があります。
(i) X=0となる確率P(X=0)
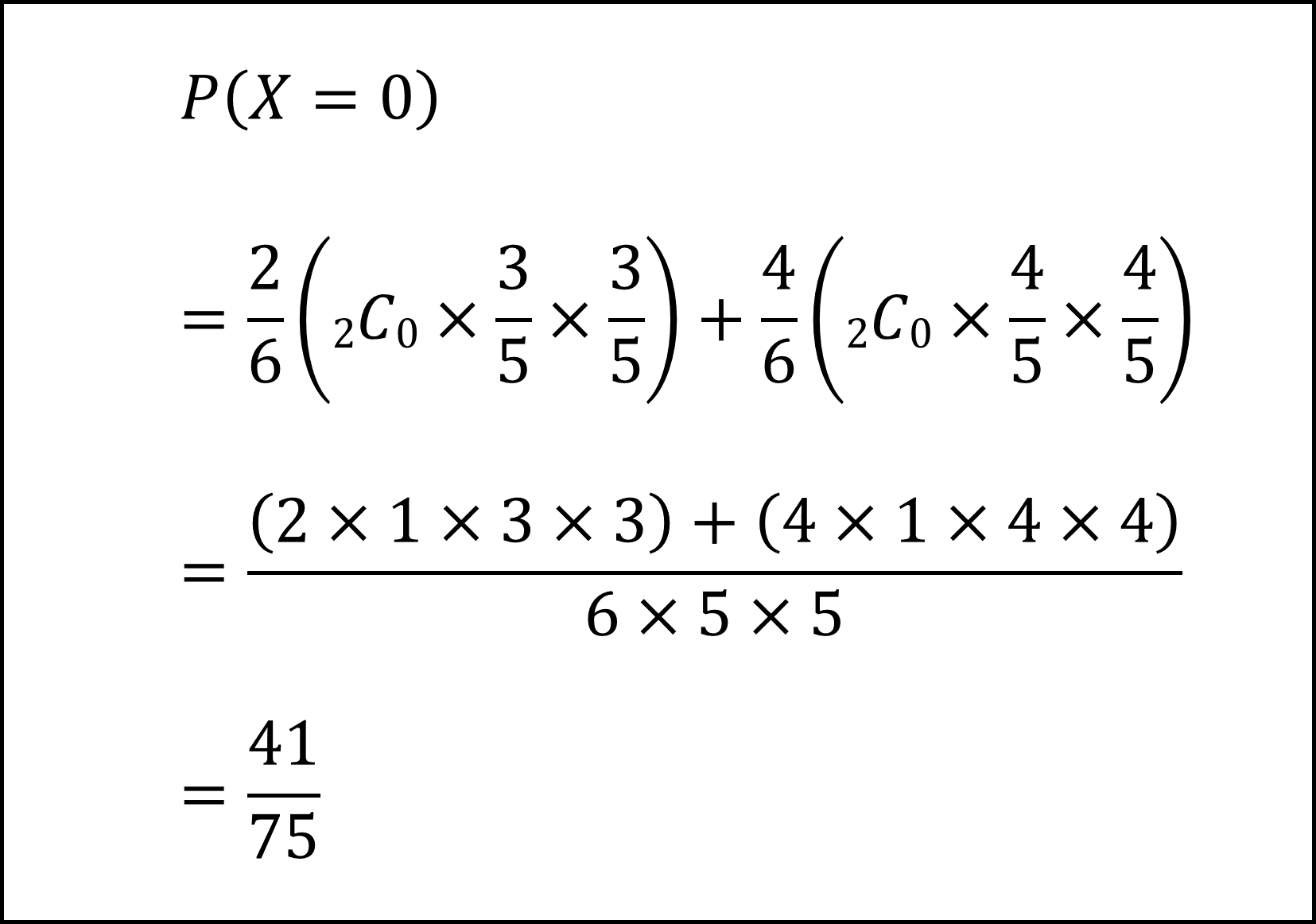
(ii) X=1となる確率P(X=1)
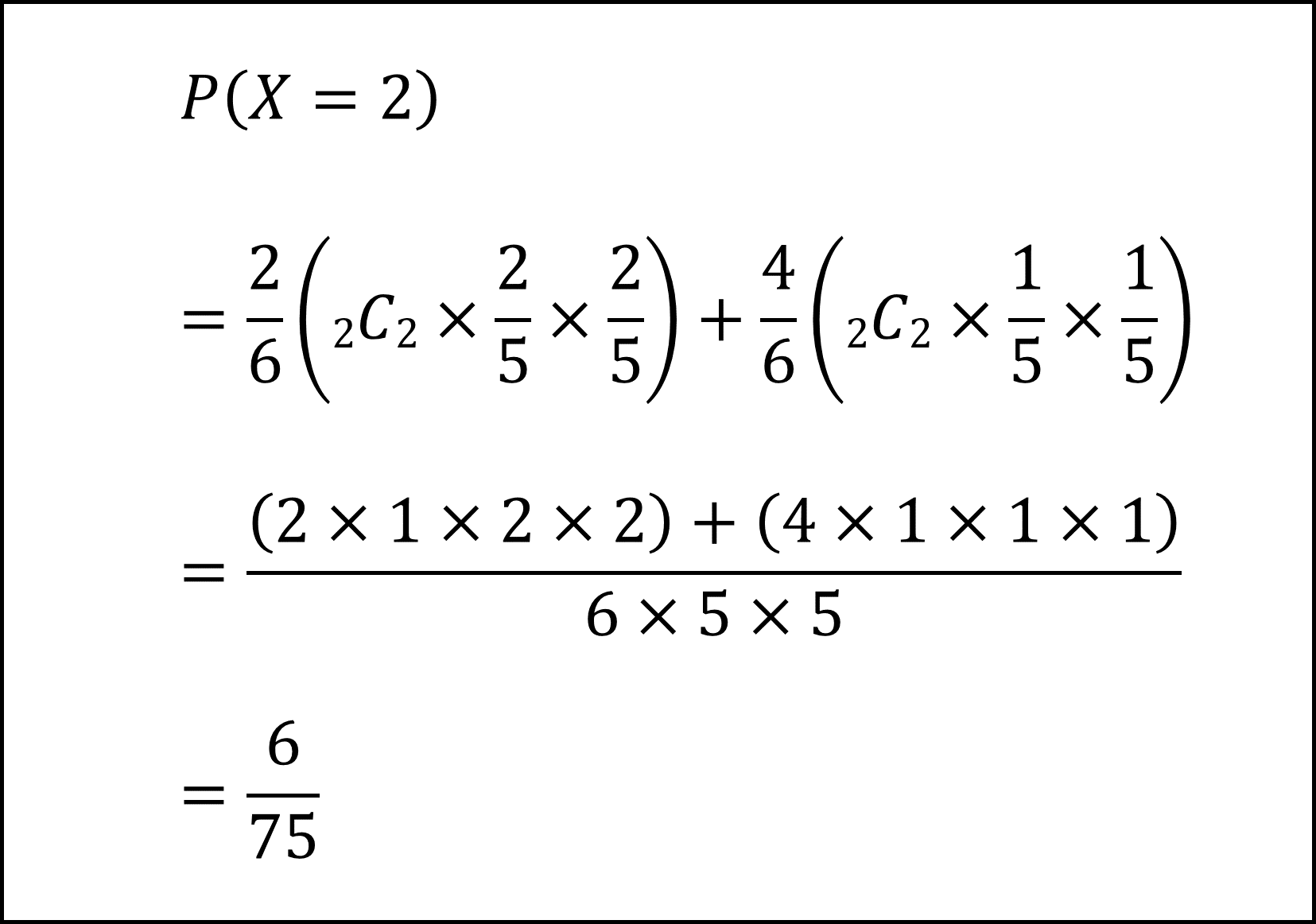
(iii) X=2となる確率P(X=2)
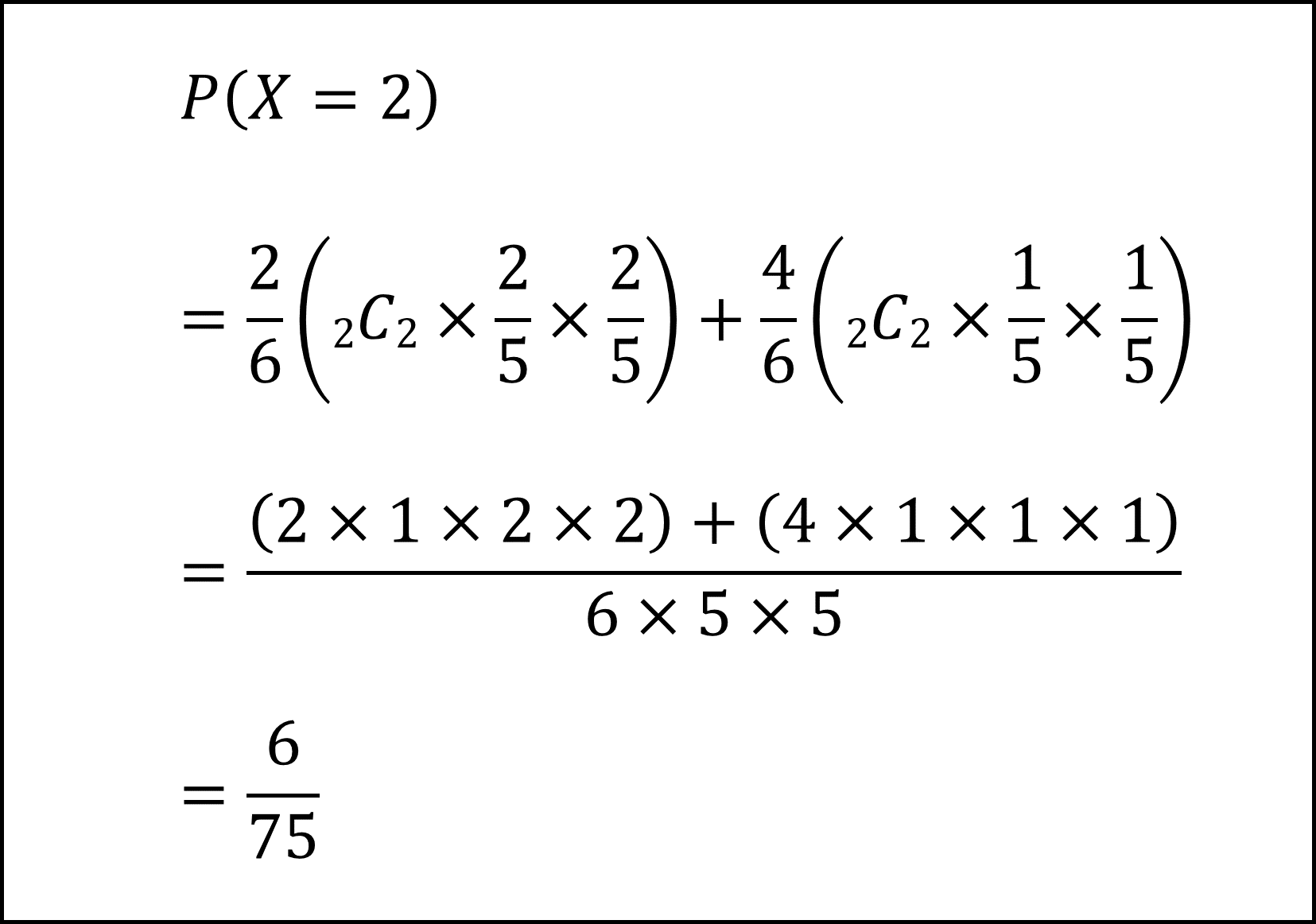
よって期待値E[X]は以下のように計算できます。
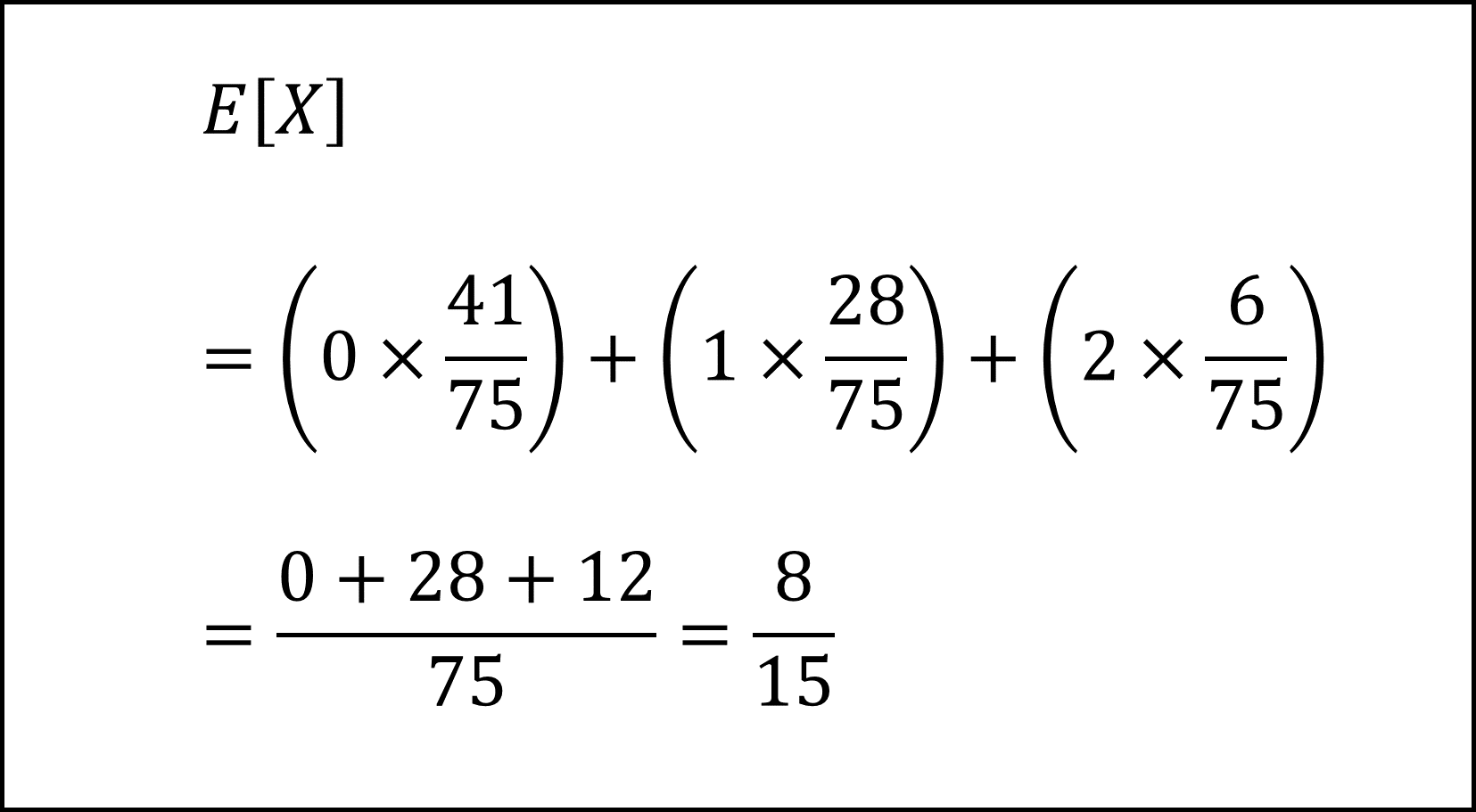
補足
- 袋Aと袋Bに分けて二項分布の期待値がn×pであることを用いても計算できます。その場合、計算式は以下のようになります。
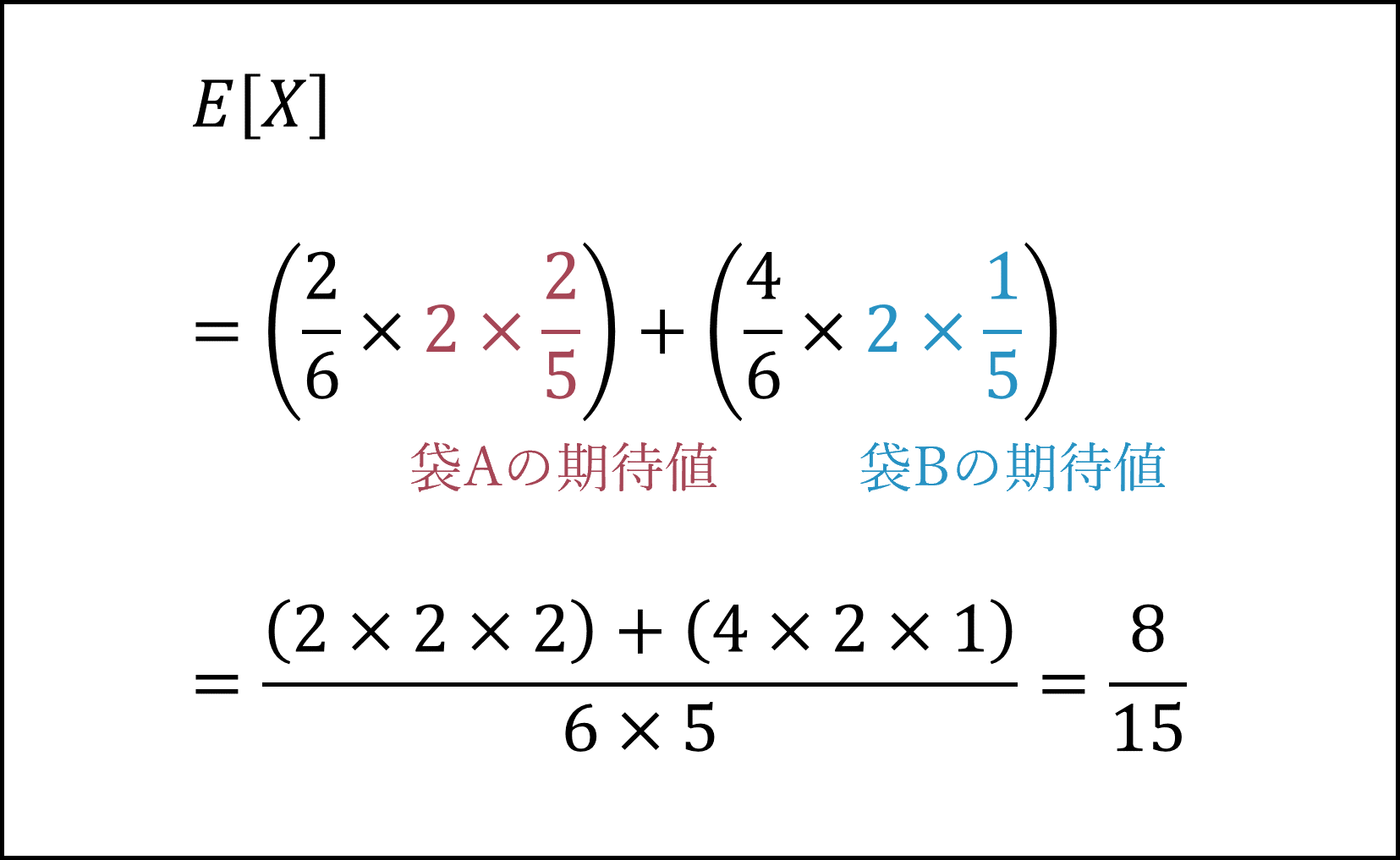
問09 [16,17番](2019年6月試験)
テーマ
- 確率変数
- 期待値
- 分散
- 共分散
正答
[16番]選択肢③ [17番]選択肢④
解答例
[16番] 公式を用いて計算しましょう(公式ありきで少々不本意ですが…)。
まず共分散は以下の公式を用います。
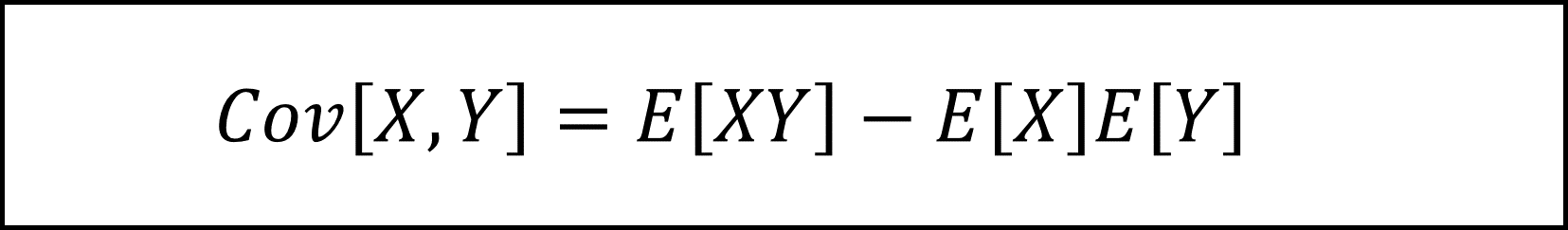
具体的には以下のように計算します。
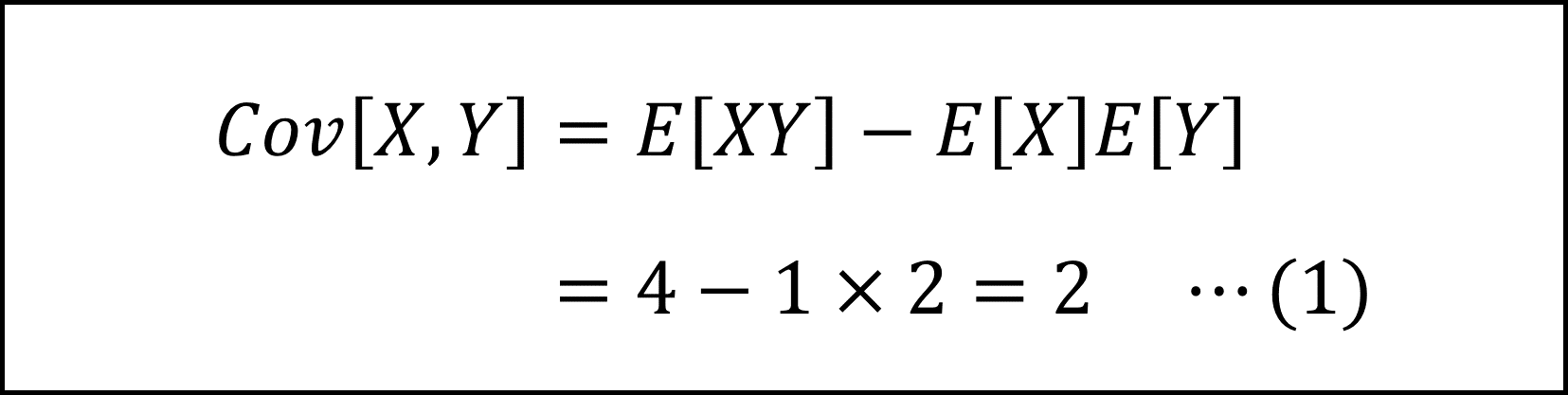
E[X^2]およびE[Y^2]は、分散に関する以下の公式を用います。
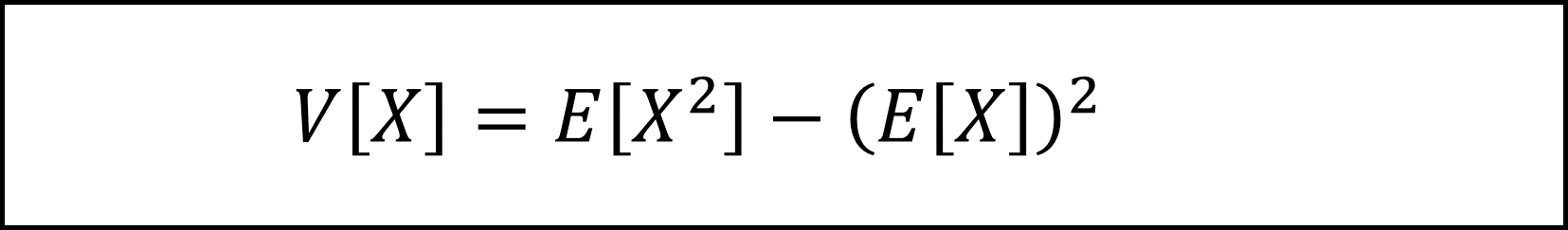
具体的には以下のように計算します。
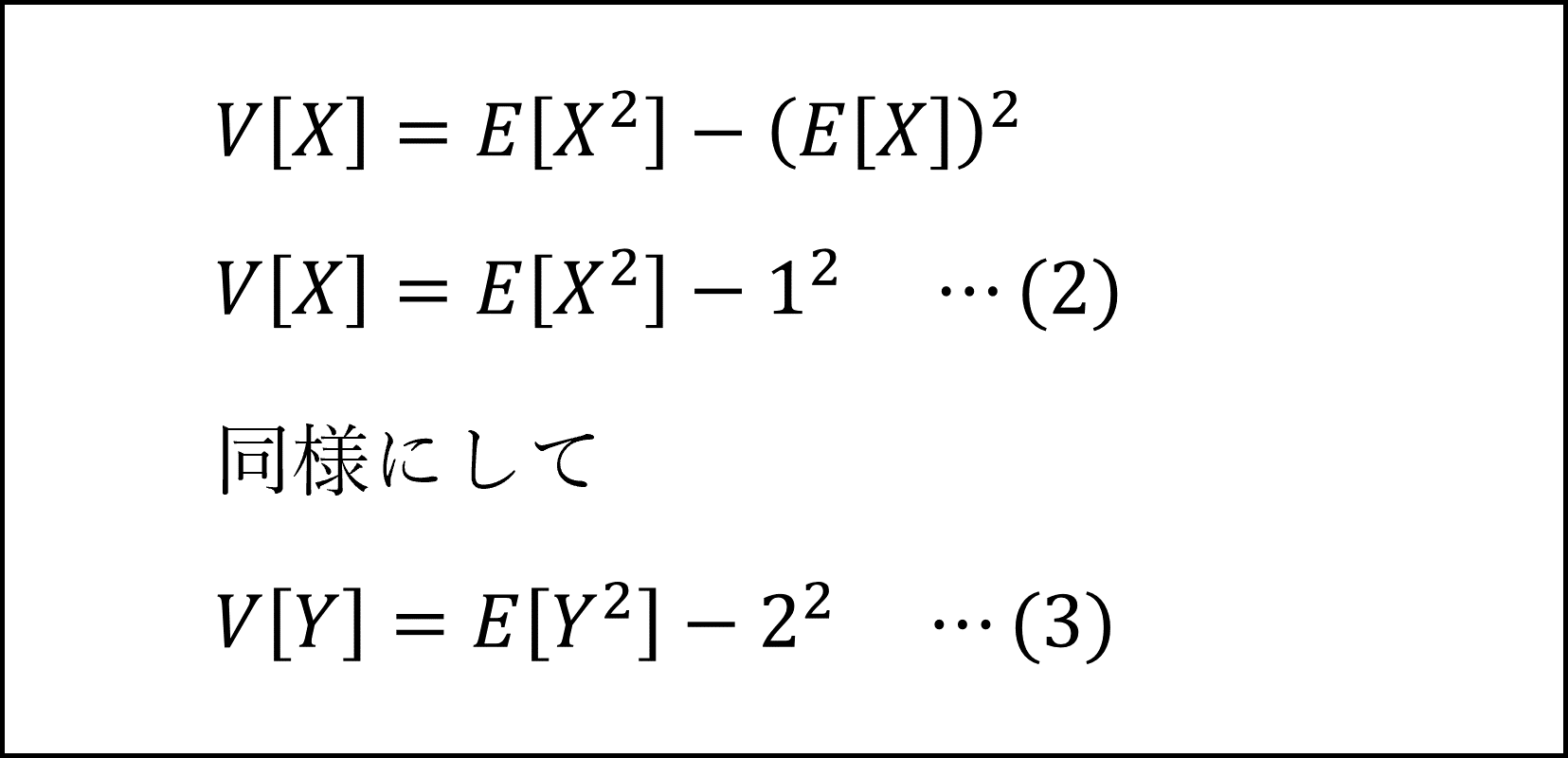
ここで、(2)式と(3)式を足した式を用いて以下のように整理できます。

また、(2)式の両辺に4を掛けたものと(3)式を足した式を用いて以下のように整理できます。

(4)式と(5)式をともに満たす選択肢は③となります。
[17番] 相関係数は[16]で求めた情報を用いて以下のように計算できます。
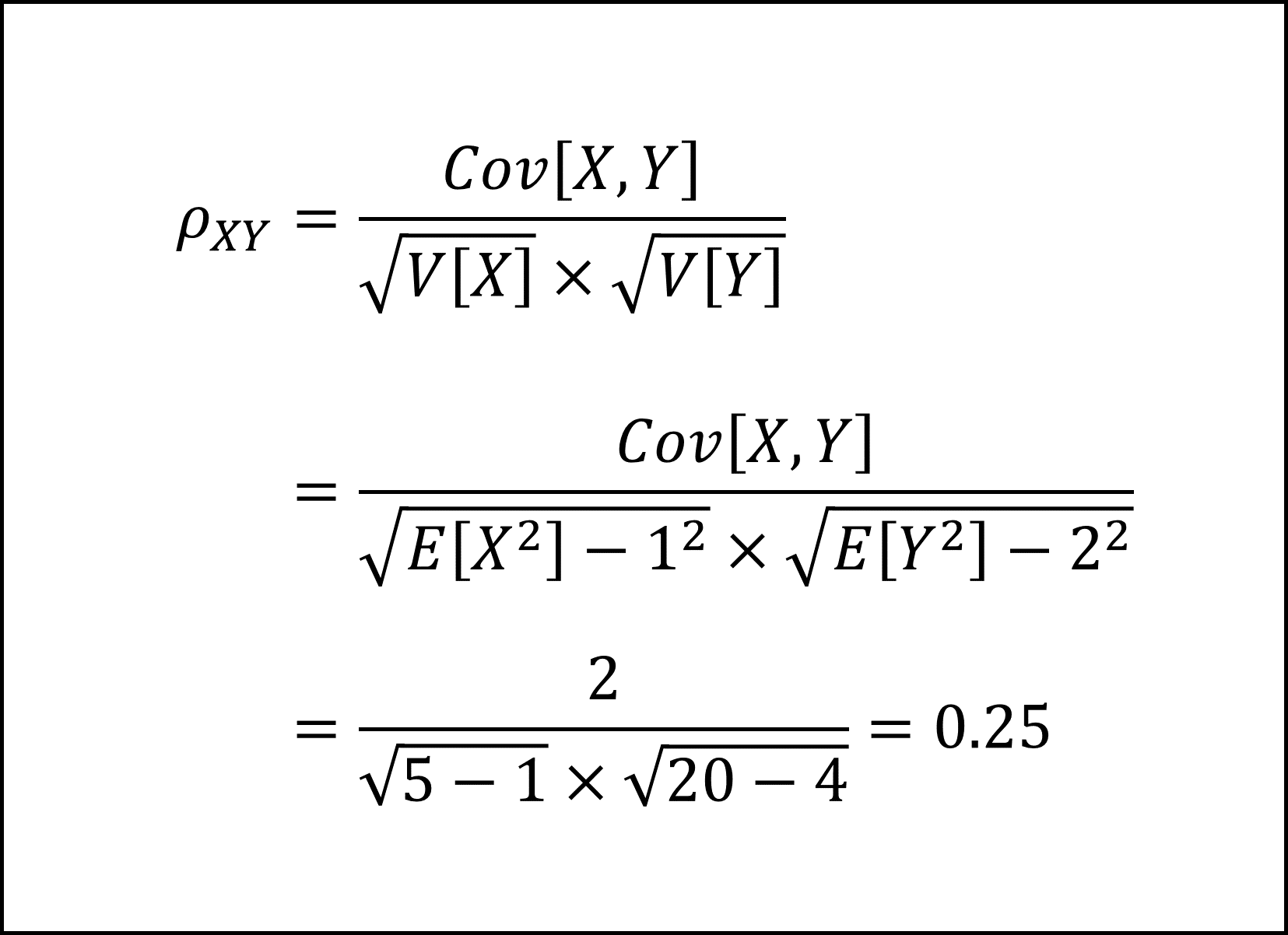
補足
- 分散の公式は少々覚えづらいですが、分散が「”母平均μからの偏差の2乗”の期待値」であることを意識すれば、まず2乗の期待値(E[X^2])が登場することに気づけそうです。
- 共分散の公式も、共分散が「”母平均からの偏差の積”の期待値」であることを意識すれば、まず積の期待値(E[XY])が登場することに気づけそうです。
問10 [18,19番](2019年6月試験)
テーマ
- 事象と確率
- 余事象
- 幾何分布
正答
[18番]選択肢① [19番]選択肢②
解答例
[18番] 3軒目の訪問で初めて調査対象者が在宅している確率は、「1軒目が非在宅の確率×2軒目が非在宅の確率×3軒目が在宅の確率」ですので
0.8 × 0.8 × 0.2 = 0.128 ≒ 0.13
となります。
[19番] 初めて調査対象者が在宅しているまでに訪問する軒数をXとすると、Xは初めて成功する(最初に調査対象者が在宅である)までの試行回数(訪問軒数)ですので、幾何分布にしたがいます。
成功確率p=0.2ですので、幾何分布の期待値と分散の公式から
- 期待値=1/p=5
- 分散=(1-p)/p^2=0.8/0.04=20
となります。
補足
仮に幾何分布の期待値と分散の公式を覚えていなくても、例えば「サイコロを振って初めて1の目が出るまでの試行回数はどれくらいと期待されるか」と考えると大体6回くらい(=1/(1/6)=6回)と思い至りそうです。サイコロやコインなどの身近な例で考えると思考が進むことがよくあるので、迷ったら試してみてください。

