統計検定®2級では指数・対数の理解が必要なトピックがいくつかあります。そこで、本記事では指数・対数について、統計検定®2級レベルにおける最低限おさえておきたいポイントを解説します。
指数・対数とは
ある実数aをm乗(am)するとき、mを「aの指数(exponent)」と呼びます。ある数を「何乗するか」を「指し示す」ような数、とイメージしておくと覚えやすいかと思います。例えば、2の3乗(23)における指数は3となり、5の2乗(52)における指数は2となります。
また、ある実数aをm乗してMとなる(am=M)とき、mを「Mのaに対する対数(logarithm)」と呼びます。ある数が別の数の「何乗に対応するか」を示す数とイメージしておくとよいかと思います。例えば、2の3乗は8(23=8)ですので、「8の2に対する対数」が3である、ということになります。
対数は一般にlogという特有の記号を用いて表記します。具体的には、実数aをm乗してMとなる(am=M)とき、「Mのaに対する対数(logarithm)m」を「logaM」と表記します。つまり、m=logaMとなります。
このように、対数を用いることで、指数mを求めるかたち(「m=logaM」というかたち)で式を表現することができる、という点がポイントになります。
指数法則
指数に関する以下の公式のことを指数法則と呼びます。

各公式の下に記載している例(ex.)とあわせて考えるとわかりやすいかと思います。
補足
なお、「2の”3分の1乗”(2(1/3))」は、言い換えると「3乗して2となる値」となります。
これを一般化して表現すると「xの”a分の1乗”(x(1/a))」は、「a乗してxとなる値」となります(以下の画像もご参照ください)。

試験では3乗以上の累乗根(a分の1乗)を計算できる電卓を使えません。仮に累乗根の計算が必要な場合には「xの”a分の1乗”」を「a乗してxとなる値」と読みかえることで探索的に値を導くことができます。
(例)「12の3乗根(3分の1乗)を計算しなさい」→「3乗して12となる値を電卓で探しなさい」
※電卓で探索することが統計学の本質ではありませんので、累乗根の計算を求められるような問題が出題される可能性は低いように思います。
常用対数
対数は「log」という記号を用いて表記するものでした。具体的には、実数aをm乗してMとなる(am=M)とき、「Mのaに対する対数(logarithm)m」を「logaM」と表記します。つまり、m=logaMとなります。
ここで、aが10の場合を考えてみると、10をm乗してMとなる(10m=M)とき、「Mの10に対する対数(logarithm)m」を「log10M」と表記します。つまり、m=log10Mとなります。例えば、m=3とすると、m=log10Mは以下(水色箇所)のように表記されます。

1行目の式は「10の3乗=1000」であることを表現しています。2行目の式は「3=底が10のときの1000の対数」であることを表現しています。
1行目「103=1000」では指数は脇役のようなイメージですが、2行目では「m=log10M」のかたちで表現され、指数が主役になっているイメージになります。
この1行目から2行目への変換を「対数をとる」といいます。そして、log記号の右下に添えられた「10」を「底」と呼び、上記のような底が10の対数を常用対数と呼びます。
自然対数
以下のような底がeの対数を自然対数と呼びます。
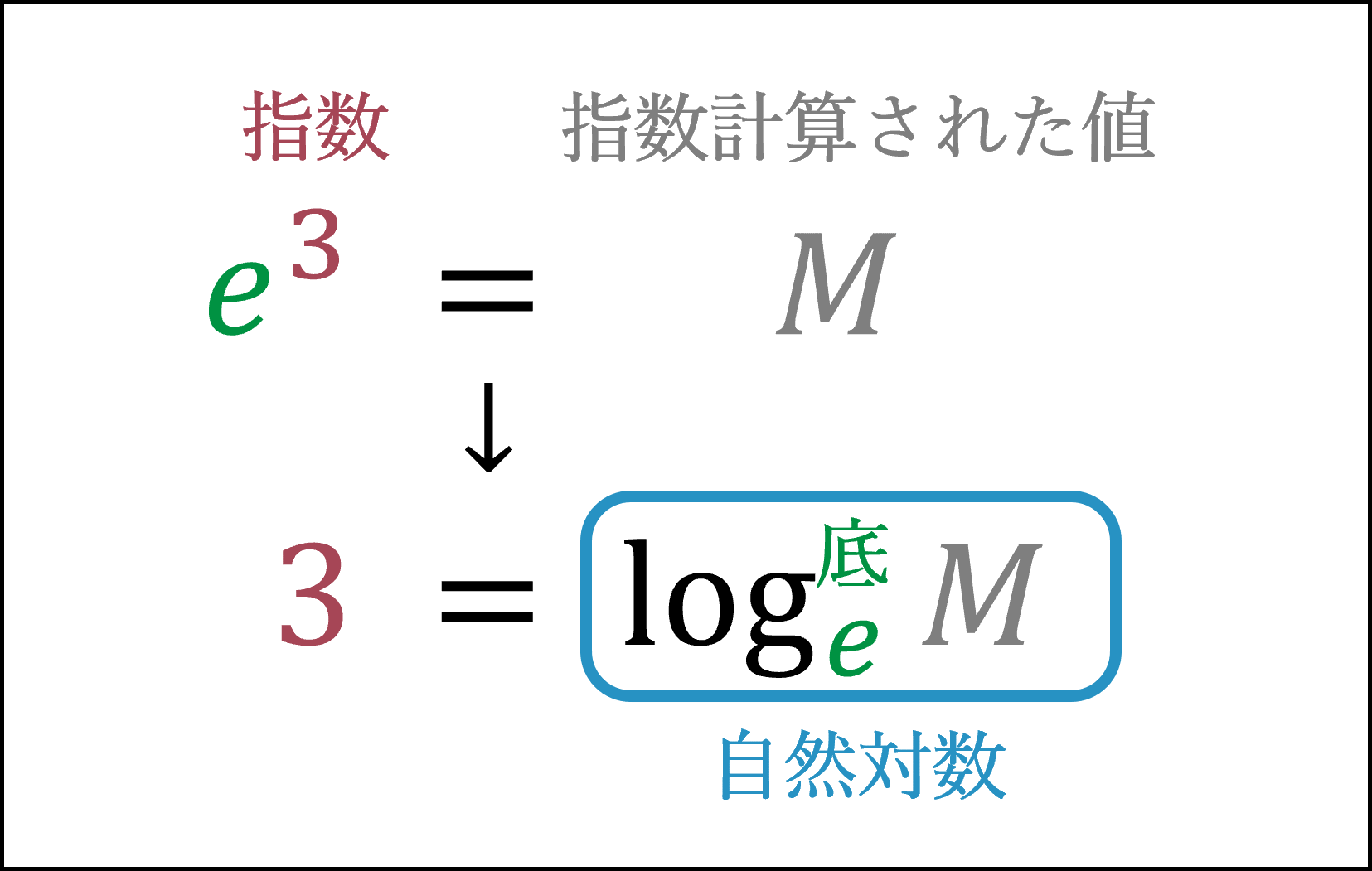
eというのは「ネイピア数」とか「自然対数の底」と呼ばれるもので、具体的には2.718くらいの値です。数学や統計学において重要な性質をもつ値です。
一般に底について特に指定されずに対数をとる場面では上記の自然対数をとります。また、自然対数の底eは記載を省略されて「log M」とか「ln M」と表記されることが多いです。
(以上)

