
※統計検定®は一般財団法人統計質保証推進協会の登録商標です。また、本コースは統計検定主催社側から公認されたコンテンツではございません。
※本記事では実際の過去問の出題内容そのものは公開しておりません。実際の過去問の出題内容については『日本統計学会公式認定 統計検定公式問題集』の購入・取得のうえご確認いただくことを推奨させていただきます。
問12 [20番](2018年11月試験)
テーマ
- 母比率の信頼区間
正答
選択肢②
解答例
回答者数(n人)のうちの「ほぼ毎日利用した人(x人)」の割合(標本比率pハット=2.0%)から、その母比率の95%信頼区間を導く問題です。
まず、標本比率pハットの期待値と分散は以下のように整理できます。「ほぼ毎日利用した人(x人)」は二項分布Bin(n,p)にしたがい、E[x]=np、V[x]=np(1-p)であることに注意しましょう。
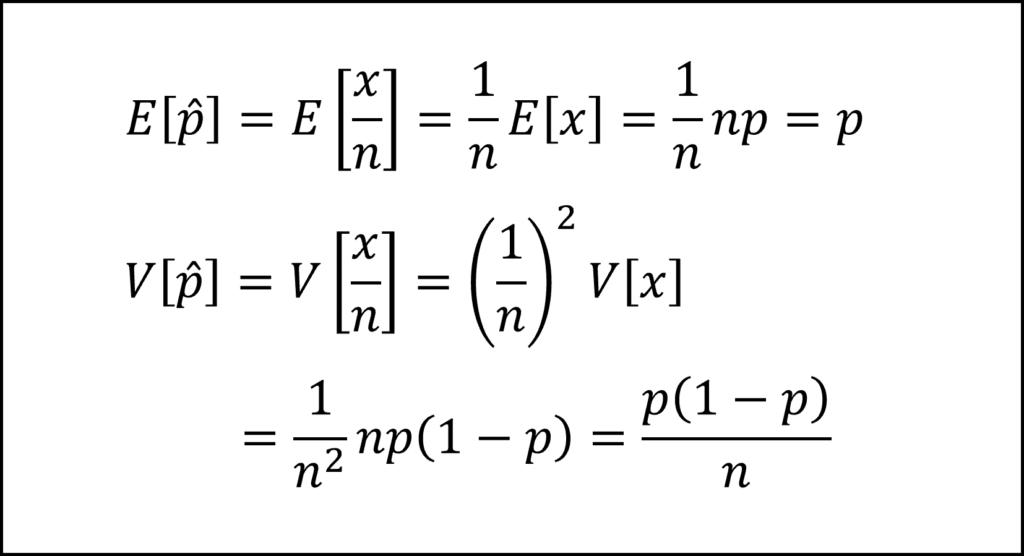
ここで、サンプルサイズnが十分に大きいことから標本比率pハットは正規分布にしたがいます。これを標準化して標準正規分布にしたがうかたちとすることで、母比率pに関して以下のような確率95%の式を導けます。
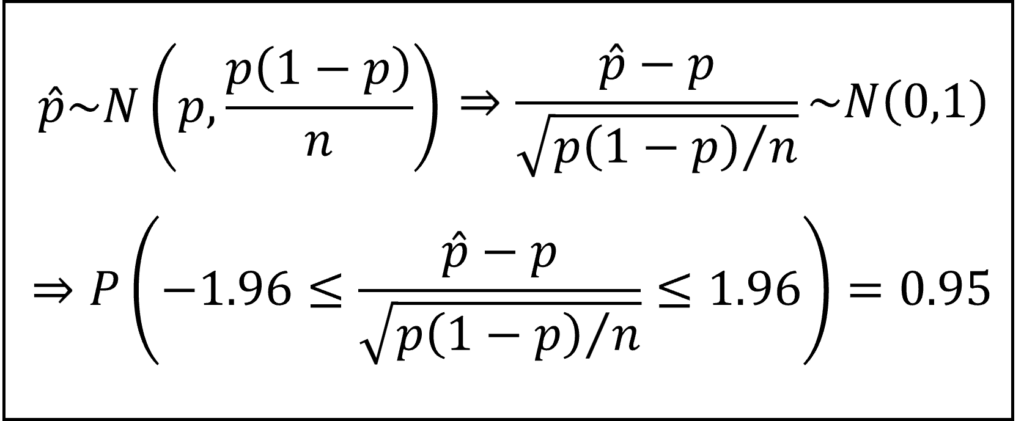
左辺の不等式を母比率pについて整理すると、母比率pの95%信頼区間を以下のように導けます。
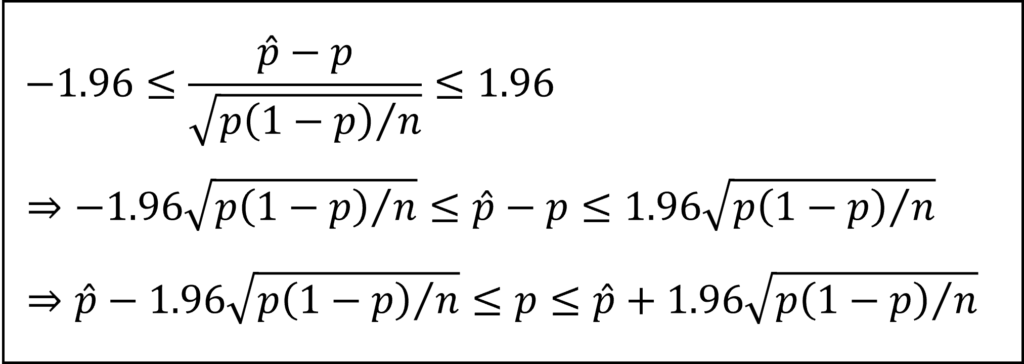
この式において、pハット=2.0%(=0.02)を代入して整理することで、本問における95%信頼区間を計算できます。なお、サンプルサイズが十分に大きいことから、平方根のなかの母比率pを標本比率pハットの値で代用する近似計算法により計算しています。
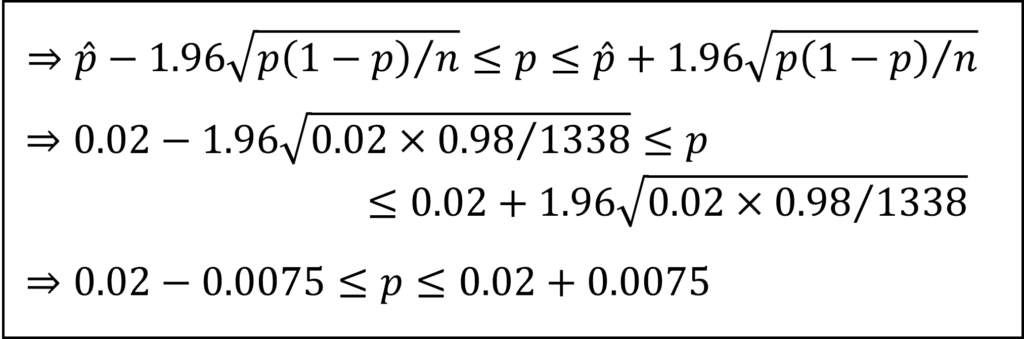
選択肢のうち最も近い値となる選択肢②が正答となります。
補足
- 母比率の区間推定は計算が煩雑でミスが多くなりやすいので注意しましょう。
- 本番では、信頼区間の式を1から導出している時間がもったいないので、信頼区間の式を記憶しておきたいところです。
問13 [21番](2018年11月試験)
テーマ
- 母分散未知のときの母平均の仮説検定
正答
選択肢④
解答例
じゃがいもの重量の標本平均をxバーとすると、標本平均の分布を以下のように整理できます。標本平均の性質より、標本平均の期待値は母平均に等しく、標本平均の分散は母分散をサンプルサイズnで割った値と等しくなることに注意しましょう。
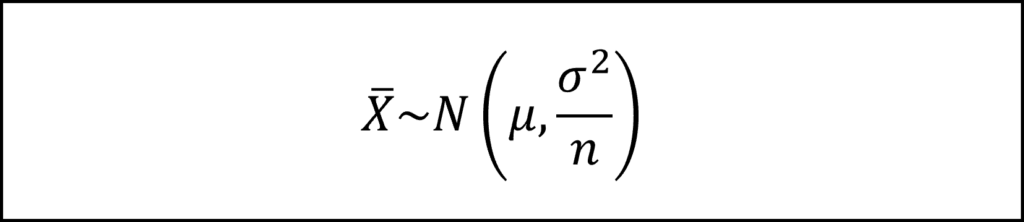
ここで、標本平均を標準化することで、標準正規分布にしたがうかたちにします。
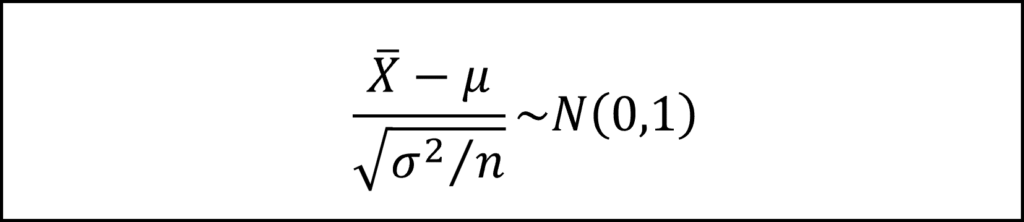
この式の母分散σ^2の部分を不偏分散s^2で置き換えると、自由度n-1のt分布にしたがうかたちとなります。
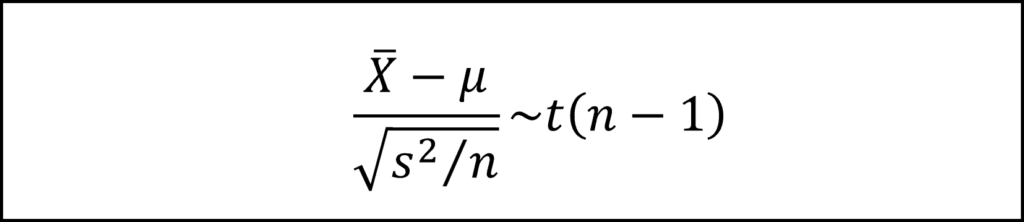
この式に、問題文から標本平均xバー、母平均μ、不偏分散s^2、サンプルサイズnを代入すると、検定統計量tの式は以下のようになります。
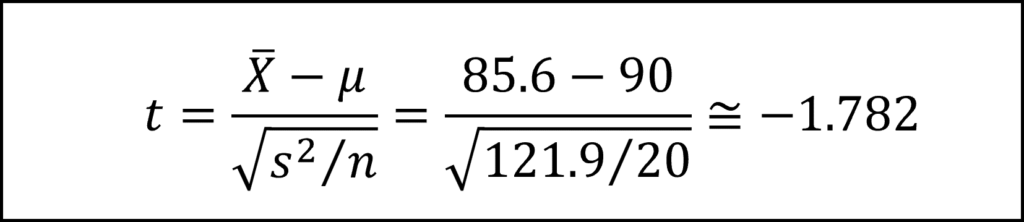
この式が自由度n-1=20-1=19のt分布にしたがいます。有意水準5%の両側検定であることに注意すると、棄却域の境界値は自由度19のt分布の上側2.5%点、下側2.5%点となり、付表より|t|>2.093と確認できます。
先ほどの検定統計量tの値は棄却域に入りませんので、帰無仮説は棄却されません。
補足
- 基本的な内容ですのでミスせずに得点できるようにしたい問題です。
問14 [22,23番](2018年11月試験)
テーマ
- 分散分析
- 検定統計量F
- 多重検定
- 第1種過誤の確率
正答
[22番]選択肢⑤ [23番]選択肢④
解答例
[22番]ここでは不偏分散の比が自由度(m1,m2)のF分布にしたがうことを利用しています。第1自由度m1は分子の不偏分散の自由度30-1=29、第2自由度m2は分母の不偏分散の自由度31-1=30となります。
[23番]互いに独立な仮説検定を3回繰り返したときの、全体としての第1種の過誤の確率を問う問題です。
第1種の過誤の確率は「帰無仮説が正しいのに、帰無仮説を棄却してしまう確率」ですので、ここでは、「A,B,Cの分布の分散がすべて等しいのに、3回の仮説検定のうち1回は棄却してしまう確率」となります。
「3回の仮説検定のうち少なくとも1回は棄却してしまう確率」は「1から3回とも棄却されない確率を引いた値」となりますので、求めたい第1種の過誤の確率を以下のように計算できます。

補足
- 自由度は(端的には)計算に用いる「データの数(サンプルサイズ)-推定値の数」で計算されます。
- 不偏分散の計算には「標本平均」という推定値を1つ用いますので、その自由度はn-1となります。
- [23番]は多重検定の弊害を念頭に置いた問題です。「3回のうち少なくとも1回は棄却される確率」は「1から3回とも棄却されない確率を引いた値」であることがポイントです。
問15 [24,25,26番](2018年11月試験)
テーマ
- 母比率の仮説検定
- 母比率の差の仮説検定
正答
[24番]選択肢③ [25番]選択肢② [26番]選択肢⑤
解答例
[24番]A社の回答が正しいとき、Xは試作品数n=200、不良品率r=0.05(5%)の二項分布にしたがいます。
二項分布の平均(期待値)はnr、分散はnr(1-r)ですので、Xの平均(期待値)はnr=200*0.05=10個、分散はnr(1-r)=10*0.95=9.5となります。
※一般に二項分布の成功確率は記号pを用いて表記しますが、次問の問題文にて記号rが用いられていることから、ここでもrを使用しました。
[25番]標本の不良品率(つまり、標本比率)をrハットとすると、以下の検定統計量が近似的に標準正規分布にしたがいます。
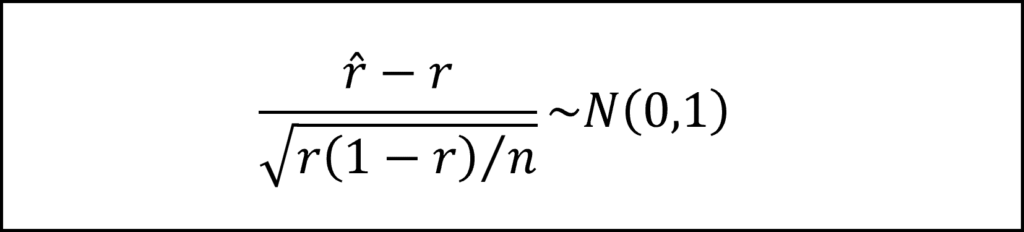
200個のうちの16個が不良品とのことなので、標本の不良品率(つまり、標本比率)rハットは16/200=0.08となります。また、帰無仮説はr=0.05で、サンプルサイズはn=200ですので、上記の検定統計量の実現値は以下のようになります。
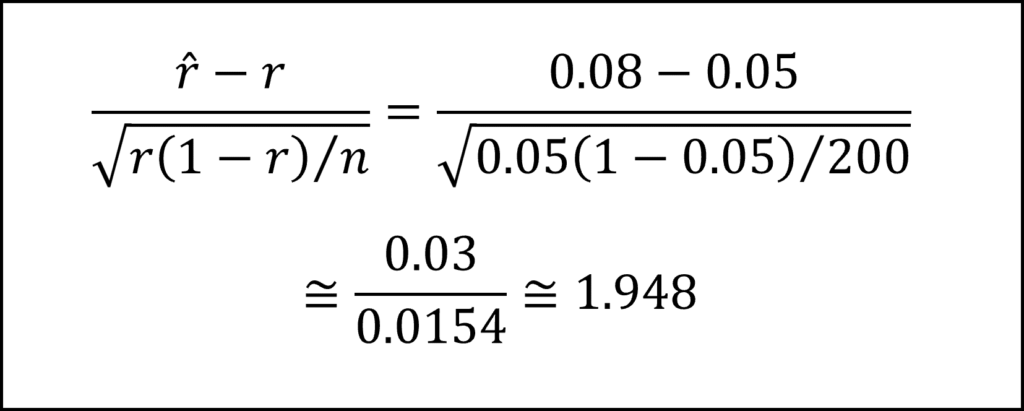
標準正規分布の付表より1.948の上側確率は0.0256から0.0262とわかりますので、正答は選択肢②となります。
[26番]不良品率の差(母比率の差)をdとし、試作品の不良品率の差(標本比率の差)をdハットとすると、以下の検定統計量が近似的に標準正規分布にしたがいます。
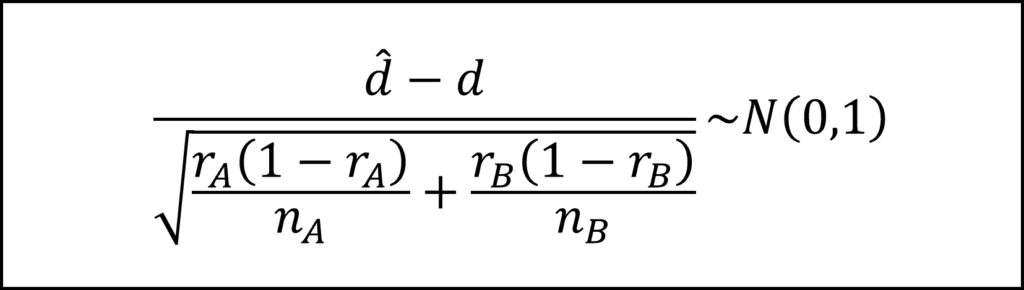
なお、rAはA社の不良品率(母比率)、rBはB社の不良品率(母比率)、rAハットはA社の試作品の不良品率(標本比率)、rBハットはB社の試作品の不良品率(標本比率)、nAはA社の試作品の個数、nBはB社の試作品の個数を表しています。
ここで、A社の試作品の不良品率は前問より0.08で、B社の試作品の不良品率は17/200=0.085ですので、その差であるdハット=0.08-0.085=-0.005となります。
また、nAおよびnBは200個です。
さらに、分母の母比率rAおよびrBを、各々、試作品の不良品率(標本比率)rAハット=0.08、rBハット=0.085で近似的に置き換えて計算すると、検定統計量の実現値は以下のように導けます。

標準正規分布の付表より0.1828の上側確率は0.4247から0.4286とわかりますので、その両側確率はその2倍でおよそ0.86となります。したがって、正答は選択肢⑤となります。
補足
- 母比率の仮説検定や母比率の差の仮説検定の難所は「①標本分布を整理するプロセスの理解」と「検定統計量のミスのない手計算」です。
- せっかく標本分布を整理できても計算ミスをしてしまうともったいないので、計算の練習もしておきたいです(とくに検定統計量の分母の計算が非常に煩雑…)。
問16 [27,28番](2018年11月試験)
テーマ
- 適合度検定
- カイ二乗統計量の自由度
正答
[27番]選択肢① [28番]選択肢③
解答例
[27番]適合度検定におけるカイ二乗検定統計量は、カテゴリーの数をk、カテゴリー番号をi、i番目のカテゴリーの観測度数をOi、i番目のカテゴリーの期待度数をEi、とすると、以下の式で表されます。
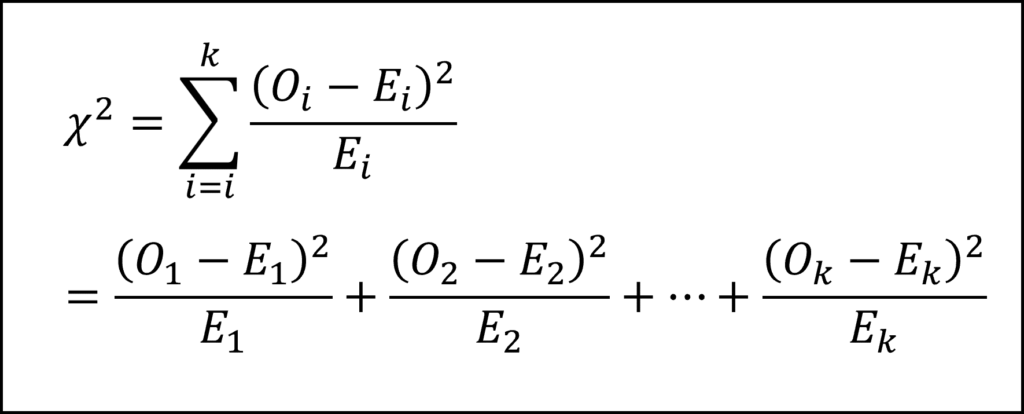
この式において、カテゴリー数をk=6とし、観測度数と期待度数の各値を代入することで選択肢①が正答と導けます。なお、帰無仮説を「発生率は曜日に依存しない」としていることから、各曜日の発生件数の期待度数は等しく102/6=17となることに注意しましょう。
[28番]適合度検定のカイ二乗検定統計量は自由度k-1のカイ二乗分布にしたがいます。
ここではカテゴリー数がk=6ですので、自由度はk-1=6-1=5となります。
また、自由度5のカイ二乗分布の上側5%点は、付表より11.07ですので、検定統計量の実現値2.59(問題文に与えられています)が棄却域に入らず、帰無仮説は棄却されません。
補足
- (応用)適合度検定の自由度はカテゴリー数kから1を引いた値となりますが、仮に帰無仮説が「ポアソン分布にしたがう」のようなものであれば、期待度数の推定にパラメータを用いることになり、用いたパラメータ数だけ自由度をさらに減じる必要がありますので注意しましょう。(ですが、2級においてはそこまでは問われないでしょう)
問17 [29,30,31番](2018年11月試験)
テーマ
- 重回帰モデル
正答
[29番]選択肢④ [30番]選択肢② [31番]選択肢④
解答例
[29番]観測データの数(サンプルサイズ、ここでは分析に用いた国の数)は、残差平方和の自由度から逆算できます。
サンプルサイズをn、説明変数の数をpとすると、残差平方和の自由度はn-p-1です。
出力結果のResidual standard error(残差の標準誤差)の部分に残差平方和の自由度(degrees of freedom)が記載されていて、ここでは「52」となっています。
したがって、求めたい観測データの数はn-p-1=52→n=52+p+1=52+2+1=55となります。
[30番]《記述Ⅰ》誤り:αは定数項(Intercept)で、その推定値(Estimate)の標準誤差(Std.Error)は出力結果より1.137e+02=1.137*10^2=113.7となります。
《記述Ⅱ》正しい:各パラメータのP値(Pr(>|t|)を確認すると、いずれも0.05以下となっていますので、有意水準5%で「0である」という帰無仮説を棄却できます。
《記述Ⅲ》誤り:自由度調整済み決定係数(Adjusted R-squared)は出力結果より0.8141です。
[31番] 《記述Ⅰ》正しい:人口密度(population)の偏回帰係数の符号はマイナスですので、(他の説明変数は同じ値で固定されていると仮定したとき)人口密度が高い国ほど自動車普及率は低い傾向にあると言えます。
《記述Ⅱ》正しい:1人あたりGDPの自然対数(logGDP)の偏回帰係数の符号はプラスですので、(他の説明変数は同じ値で固定されていると仮定したとき)1人あたりGDPの自然対数が高い国ほど自動車普及率は高い傾向にあると言えます。なお、1人あたりGDPが大きな値であるほど、1人あたりGDPの自然対数も大きな値となります。
《記述Ⅲ》正しい:推定されたモデルに人口密度=400、log(GDP)=10を代入して計算すると、自動車普及率の予測値は約448であることを導けます。
補足
- 偏回帰係数を解釈する際には「他の説明変数の値は固定されているものと仮定したとき」という仮定をおきます
- 本問では簡単に「他の説明変数が同じ値である場合」とだけ記載があり、ピンとこない(この論点を知らない)と、ここで疑問を抱いてしまうかもしれません。
問18 [32,33,34番](2018年11月試験)
テーマ
- 単回帰モデル
- 重回帰モデル
正答
[32番]選択肢④ [33番]選択肢⑤ [34番]選択肢①
解答例
[32番]《記述Ⅰ》正しい:残差平方和を自由度で割ってその正の平方根をとった値が「残差の標準誤差(誤差項の分散の不偏推定値の正の平方根)」です。残差の標準誤差は0.608と表中にあり、その自由度はn-p-1=5-1-1=3ですので、残差平方和は以下のように計算できます。

《記述Ⅱ》誤り:切片のt値は「切片の係数」を「標準誤差」で割った値です。単位を円にして1万倍すると、「切片の係数」が1万倍され、その「標準誤差」も1万倍されますので、結果的にt値は元の単位のときと変わりません。
《記述Ⅲ》正しい:単位を1万倍すると切片の推定値も1万倍されます。
[33番]《記述Ⅰ》誤り:説明変数として不要かどうかは、説明変数の係数の推定値の大きさではなく、
《記述Ⅱ》誤り:説明変数同士の相関係数が0.9を超えていて非常に強い相関があり、サンプルサイズも5と小さいので、多重共線性の問題を考慮する必要があります。具体的には、偏回帰係数の推計値の精度が不安定になります。
《記述Ⅲ》誤り:P値が0.559ということは、帰無仮説正しいときに、検定統計量の実現値が、その値、および、その値よりも起こりづらい値をとる確率が55.9%もあるということです。帰無仮説が正しくないとは言いづらく、帰無仮説を棄却できません。
[34番]《記述Ⅰ》誤り:2つのモデルは異なる説明変数を用いた異なるモデルによる分析ですので、同じ説明変数の係数だからと言って同じ値になるわけではありません。
《記述Ⅱ》正しい:前者のモデルでは回帰係数bのP値は0.07であるため有意水準10%で有意と言え、後者のモデルの回帰係数b’のP値は0.559であるため有意水準10%で有意とは言えません。
これはつまり、zという説明変数を含めて分析すると、xとyに有意な関係性がないということで、zを加える前に表出していたxとyの関係性は「見かけ上の関係性(擬相関)」であった可能性があります。
《記述Ⅲ》誤り:後半の文章が誤りです。b’は有意水準10%で有意でないので、xとyのあいだには有意な関係性があるとは解釈できません。
補足
- 単回帰分析に説明変数を加えて重回帰分析を行う問題は、論点が多くあり問題作成しやすいので、出題されやすい問題であると予想されます。

