
私たちが日常で目にするデータの多くは、必ずしも「正規分布」というきれいな釣鐘型の分布をしているわけではありません。特に、成功・失敗のどちらかしか起こらない「ベルヌーイ分布」のような二値の確率モデルは、その形が非常に単純である一方、正規分布とはほど遠い非対称な分布であることが多いです。たとえば「コイントスで表が出る確率が0.7」というような設定で考えれば、0または1しか取り得ないわけですから、そのヒストグラムは左右対称どころか、いかにも“0か1か”のギザギザしたものになります。
ところが、ベルヌーイ分布を母集団(真の分布)とし、その中から複数回サンプルを取り出して平均を計算していくと、不思議なことに正規分布らしい釣鐘型が見えてきます。これが有名な「中心極限定理」の示す現象です。今回のブログでは、母集団のベルヌーイ分布(成功確率0.7)から標本サイズを100とって、さらにそれを1000回繰り返して得られた標本平均の分布を可視化してみます。
母集団は「0か1か」のベルヌーイ分布
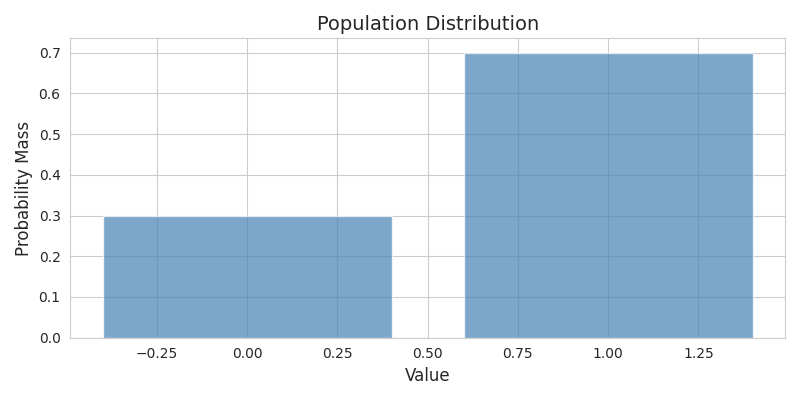
まずは母集団の分布を示す図1をご覧ください(図1:母集団の分布)。これは成功確率が0.7のベルヌーイ分布なので、値が1になる割合が0.7、0になる割合が0.3となっています。縦軸には確率が表示され、それぞれの値(0と1)がどの程度の頻度で観測されるかが視覚的にわかるようになっています。
この分布は一目でわかるように「釣鐘型」ではなく、二本の棒だけが立った非常に単純な形をしています。母平均は0.7、母分散は0.7×0.3=0.21です。こうした二値しか取らないベルヌーイ分布が、どのように正規分布に近づいていくのかが今回のテーマです。
標本をとって平均を繰り返す
次に行うのは「標本サイズ100での抽出を1000回繰り返し、それぞれの標本平均を計算する」という作業です。具体的には、母集団(成功確率0.7のベルヌーイ分布)からランダムに100個のデータを取り、その100個の平均値を計算します。これを1回の試行とし、同じ操作を合計1000回行うことで、標本平均を1000個得ることができます。なお、今回は母集団が0か1かのベルヌーイ分布なので標本平均も0から1の間の値となり、これを標本比率とも呼びます。
標本平均は、母集団の分布に関係なく、標本サイズが十分大きいほど正規分布に近似できる、というのが中心極限定理の趣旨ですが、実際のシミュレーションで確認してみると、その近似がいかに実感できるかがわかります。
図2で見る標本平均の分布:正規分布らしい形状
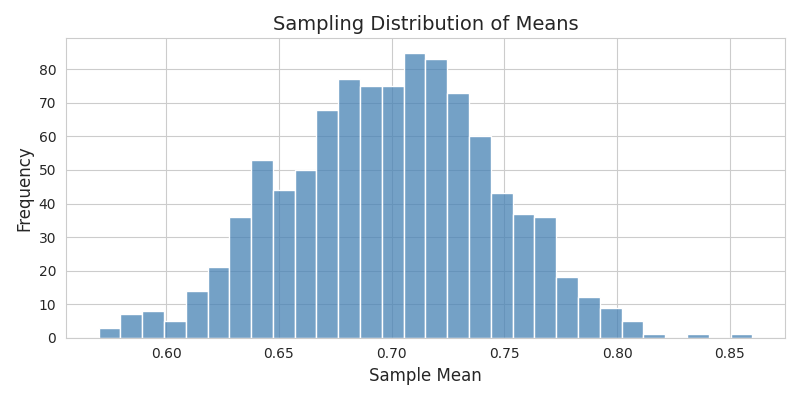
続いて得られた1000個の標本平均(標本比率)をヒストグラムにしてみたのが、図2:標本分布(n=100の標本の標本平均1000個のヒストグラム)です。ヒストグラムを描くと、横軸に「標本平均」、縦軸に「度数(頻度)」をとり、どのあたりの平均値がどれくらい出現したかを示しています。
実際にプロットしてみると、母集団の分布(図1)があれほど単純で、しかも0.7と0.3という非対称な割合だったにもかかわらず、このヒストグラムは釣鐘型に近い形状を示します。完全な左右対称というわけではありませんが、概ね真ん中あたりにピークがあり、なめらかな曲線で表現できそうな形です。ここに標本平均(標本比率)の理論的な正規分布(平均0.7、分散0.3*0.7/100=0.0021)を重ね描きしてみると、かなりよく重なることに驚かれる方もいるのではないでしょうか。
なぜ正規分布に近づくのか――中心極限定理
「母集団が正規分布でなかったとしても、標本平均は正規分布に近づく」という事実は中心極限定理と呼ばれ、統計学のなかでも特に重要な定理の一つです。ざっくり言うと「データの足し合わせ(あるいは平均)は、元の分布の形に依存せず、サンプルサイズが十分大きいほど正規分布に近づく」というものです。ベルヌーイ分布のような極端な例でも、標本サイズを増やすほど正規分布に近づいていく様子は、非常にわかりやすいサンプルケースと言えます。
もう少しだけ数式に触れるなら、ベルヌーイ分布の母平均は0.7、母分散は0.7×0.3=0.21でした。標本平均の分散は「母分散 ÷ 標本サイズ」なので、0.21を100で割って0.0021になります。その平方根が標準偏差、つまり標準誤差となり、これは約0.046です。図2のヒストグラムも、この標準誤差をもとに描いた正規分布と比較すると、中心付近で最も多く観測され、そこから離れるにつれて徐々に頻度が下がっていく、という正規分布特有の傾向が見事に再現されています。
シミュレーションで学ぶ統計学の面白さ
今回の例で注目していただきたいのは、母集団が「二値しか取らないベルヌーイ分布」であっても、標本平均をとることで釣鐘型に近い分布が浮かび上がる、という点です。これは「理論としては知っているけれど、本当にそうなるの?」と疑問をもたれがちな話でもあります。シミュレーションとして実際にコードを書き、ヒストグラムを描いてみることで、教科書で読むだけでは味わえない「統計の妙」を体感できます。
さらに、もし標本サイズnをもっと小さくしたり、逆に大きくしたりするとどうなるかを試してみるのも面白いでしょう。n=10程度だとまだ分布のばらつきが大きく、釣鐘型というよりはいびつな形になるかもしれません。n=1000といった桁で試すと、もうかなり正規分布にそっくりになります。統計解析では、こうした標本サイズの設定が推定の精度や検定結果に大きく影響するため、中心極限定理を理解しておくことが欠かせません。なお、このようなシミュレーションを実行するツールを以下のページにご用意していますので、試しにぜひ利用してみてください。

実務への応用とまとめ
実際のデータ分析では「母集団の分布は不明だが、標本平均の扱いは正規分布を仮定してもよい」という場合が多々あります。これはまさに中心極限定理によって支えられている理論的根拠です。A/Bテストなどで「ユーザーのクリック率」や「コンバージョン率」を比較するときにも、各グループのベルヌーイ(成功/失敗)データをたくさん集め、その平均(=割合)の分布を正規分布近似して、差があるかどうかの検定を行う、といった手法がよく用いられます。
今回のブログでは、図1に示したベルヌーイ分布を母集団として、標本サイズをn=100、抽出回数を1000回繰り返して得られた標本平均のヒストグラム(図2)を観察しました。その結果、二値しか取らないような歪んだ分布でも、標本平均をとると見事に釣鐘型が現れることが確認できます。統計学を学び始めると必ず耳にする中心極限定理ですが、実際にシミュレーションを通じて「こんなにもはっきり形が変わるんだ!」と体験すると、理解がぐっと深まるのではないでしょうか。もし機会があれば、ぜひ別の分布(例えばサイコロの目の分布=一様分布など)でも同様に標本平均をとってみて、「なぜか正規分布が姿を現す」不思議な光景を楽しんでみてください。

